このページは 東北学院大学 工学部 機械知能工学科 １年生の講義「コンピュータ応用」(Ｂ組＝後半)用のオンラインページ兼、講義ノート兼、講義立案兼、メモなどのページです。(すなわち常に工事中)

基本的にはこのページの内容に沿って講義を行っていきますが、だからといって、これに目を通したことで授業を休んだりサボったりしていい理由にはなりません（自分の経験値向上になるかどうかで判断してください）。 逆に、このページをみることも義務づけはしません。 講義を受ける前の予習(ページ執筆が間に合えば)や、講義内容の補填などに使ってください。 注意事項の詳細をまず確認してください。

講義をうけるにあたっては、「自分の手で試すこと」に重きをおいてください。
コンピュータの上のことです。 やろうと思えば友達から完成済みのプログラムをもらうなど、手書きでレポートを書くのに比べれば圧倒的に楽に手抜きができます。 しかし、それがなんの得にもならないことは自明です。
単位になるかならないかを判断基準とするのではなく、今後の自分の「手段」をいかに増やすかを判断基準としてください。

シラバスにも明記しましたが、この科目は初心者を想定して進めます。 多少でもプログラミングの心得があると暇をもてあますかも知れません。 その場合は、余った時間を「自分でいろいろやってみる」ことに使ってください。

なお、講義中に講義内容と関係ないホームページなどを見ていたとしても、大人しくしている限りは文句はいいません(音出したり動画を見て画面をチカチカさせたり隣に迷惑をかけたら退出)。 ただし、その場合は「私には余裕があります」という宣言と見なし、成績評価で妥協しないことにします。

この講義の目的

この講義の目的は

• コンピュータを計算の道具として使うことを覚える
• コンピュータでできる計算手段、手法を知る

です。

もちろん、Ｃ言語のプログラミング（＝プログラム作成＝コンピュータへの直接的な指示通知法）についても多くの時間を割きますが、「Ｃ言語を学ぶこと」が第一義ではなく、あくまで手段として使い、解説します。
というのも、ほとんどの学生さんが１年次にプログラムの作り方を習ったはずなのに、結果的に卒業研究の時にはなにも覚えていないという現実があり、だったら、文法そのものに力点を置くよりも、それによって何ができるかを体験することで、「将来自分で使う日が来たときに、使えることを経験しておく」ことを優先すべき、と考えたためです。
目的さえはっきりしていれば、最低限を身につけるにはそう手間はかかりません。工学部なら。

その背景の元、

• 処理すべき内容を、個々の手順に分解する。
• それを元に処理をさせる。

を基礎として身につけ、あとは電卓でも、表計算ソフトでも、プログラムでも、目的に応じて道具を選べばいい、という発想を持ってもらえれば、と思います。

「紙を切る」ときに、手でちぎったり、はさみをつかったり、カッターを使ったりと道具は変えますし、目的に応じて向き不向きはあります。 が、「正方形の紙がほしい」というときには、切る場所を決め、そこに道具を適用するという手順の大筋は、かわりません。それと同じことです。

コンピュータとは

本講義ではコンピュータとは、おおざっぱに

• あらかじめ指定した手順に基づいて
• (主に演算)処理を行う

装置ととらえます。

今日では非常に多くの機械、装置にコンピュータが入っています。 「コンピュータ」と呼ばれている機器はもちろんのこと、携帯電話やゲーム機、ロボットにも必須の要素で、従来はただの機械だったはずの自動車、掃除機や扇風機のような家電品にもコンピュータは入っています。
「コンピュータ入り」かどうかの一つのおおざっぱな見分け方は

• 押すと「ピッピッピ」と音が鳴るようなスイッチがついている→コンピュータ入り
• 押すと「ばちんばちんばちん」とメカニカルに動作するスイッチがついている→なし

です。身の回りで「ピッピッピ」となるものの多いこと。
※もちろん、例外はいくらでもあります。機能の少ない腕時計とか

さて、電卓を考えてみましょう。これはコンピュータ入りです。 そもそも、いまのパソコンに使われるコンピュータの心臓部であるCPUと呼ばれる部品は、小型でやすい電卓を開発する過程で生み出されたことは有名な話？です。
電卓で計算するとき、計算したい内容、計算指示は使うときに行います。あらかじめではない？
電卓の中のコンピュータは「ボタンを押されたときに電卓として振る舞うよう」あらかじめ手順が仕込まれています。

パソコンも一緒です。あらかじめ、人が使うときのことを想定して、大量に処理の手順をしこまれています。電卓とパソコンの大きな違いは、性能の差もですが、「処理の手順」、いわゆるソフトウエアを後から追加できることです。
※電卓でも高級なのはしこめますが

逆に、「手順を新たに教えることができる」コンピュータは手順を教えることで、新しい仕事をさせることができるようになります。

コンピュータの大きな特徴は、

• 手順が指示されていれば、計算などを高速に処理できる。

ことです。電卓の計算でも十分、我々の手計算に比べれば十分高速ですが、表計算ソフトを使ったり、プログラムをつくることで、コンピュータに入力済みのデータ（今時の計測装置は、パソコンと直接データをやりとりできるものが多い、デジカメなども含めて）を処理できますし、少ない条件を指定し、それに合致した結果（素数を定義から求めるなど）を大量に生み出すこともできます。

それを応用した使い道をみてみましょう。

機械科におけるコンピュータの使い道

機械屋にとってのコンピュータの、計算装置としての使い方は主に以下の通りです。

• 測定データの処理、グラフ化など
• コンピュータ支援による機械設計
• コンピュータシミュレーション
• ロボットなどの制御

データの処理に使えることはすでに述べました。 膨大なデータから、ある特徴を持った部分を探し出したり、逆にどんな特徴が含まれているかを探し出すような使い方もできます。
例：車の振動データから、エンジンの回転が直接の原因の部分を取り出す。
（残りは地面からの震動かも？）

コンピュータ支援による設計は、CADと呼ばれるコンピュータ上で設計図を書く、どちらかというとお絵かきツールとしての使い方がよく知られていますが、さらに、コンピュータの中で仮想的に組み立て、ちゃんと動くか？、また思った通りに動くか？などを検証することもできます。

コンピュータシミュレーションは「計算量」という意味では圧倒的に比重の大きな使い道です。 自動車や飛行機を設計したとき、実物を作らなくても空気抵抗などを見積もったりできます。 また、機械部品を設計したとき、力をかけても壊れないか？といった確認をすることも、実物を作らなくてもほぼ検討がつきます。 コンピュータ支援設計と似てはいますが、どちらかといえばシミュレーションの方が純粋に計算です。

ロボットの制御とは、たとえば、ロボットの腕や足をどう動かすかを決めたり、実際にある角度に関節を曲げたいときに、いまの曲がり具合をもとにモータにどのくらい電気を流すかを決めたりする作業です。 このためには必要な計算を１秒間に数十〜千回ほど行う必要があります。 とてもですが、電卓をたたいたりしていては間に合わないため、あらかじめ「こういうときにはこうしなさい」というルールである「制御則」をコンピュータに教えておき、瞬間的に計算して判断して動かしてもらうことになります。
つまり、コンピュータでプログラムを作ることなくして、ロボットは動きません。

機械でコンピュータを使う理由はこんな感じです。
もちろん、このほかにもレポートを書いたり、ネットで調べ物したり、ゲームで遊んだりといったありきたりの使い方もありますが、この科目は「機械」で「コンピュータ応用」なので無視します。

コンピュータの構造

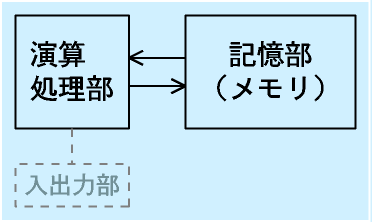コンピュータの概略構造

テレビをみるときにその構造を知っている必要はありませんが、コンピュータを使うとき、とくにコンピュータに新しく手順を覚えさせようというときは、コンピュータの構造を知っておくと、理解が進むと思います。

コンピュータは、大きく二つの重要部分があります。

• 演算処理部
• 記憶部(メモリ)

昔々のコンピュータはこの二つがはっきり分かれていたのですが、最近は性能向上のための改良が進み、簡単に分けられなくなりました。 が、おおざっぱには、パソコンで言えば、前者はCPU（MPU）、後者はメモリ（RAM：ラム）などと呼ばれている部分です。

そのほかに、キーボードやマウス、画面やネットとやりとりをする入出力部がありますが、それはおいておきます。

演算処理部は演算だけ、メモリは数字の記憶だけができます。
メモリには「処理すべきデータ」「処理した結果のデータ」など、処理する対象そのものを置きます。 演算処理部はメモリからデータを取り出し、処理して、結果をメモリに置きます。

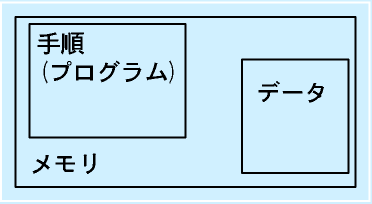メモリ上にデータと手順

演算処理部が処理をするためには「手順」が必要です。 その手順も、メモリにおいてあります。
つまり、演算処理部がやることは

1. メモリから次にするべき処理の指示（手順の一部）を持ってくる。
2. その指示に基づいてメモリとデータをやりとりしたり、演算したりする。
3. １にもどる

をひたすら繰り返すことです。これは電源が入ったときから切られるまで、とにかく続きます。 パソコンなどが何もしていないように見えても、画面が真っ黒でも、その中ではなにかしています。（何もしないでちょっと待つ、という指示もある）

おそらく、ここでいう「データ」として「数値」が思い浮かぶと思います。
一方、指示は「○○と××を足す」といった、言葉での指示がありそうです。
が、メモリは「数字だけ」、より厳密には「０と１」をひたすら大量に記憶するだけです。

「数値」については、比較的単純で、２進数と呼ばれる方法を使います。
たとえば、ゼロイチを４個集めると「００００」〜「１１１１」で１６通り（２×２×２×２）の組み合わせができます。 これに、数字の「０」〜「１５」を割り当てれば、ゼロイチだけで数値を表せます。 実際には、ゼロイチを３２個とか６４個集めて組み合わせ、整数や小数を様々に表します。
（もちろん、その組み合わせと実際の数値の間にはちゃんと規則を決めておく）

さて「指示」はというと、発想は実は一緒です。ゼロイチ４個で１６通り、というところまでは同じ。

００００(0)：足す　
０００１(1)：引く
００１０(2)：かける　
００１１(3)：割る
０１００(4)：休む　
０１０１(5)：メモリから数値をとってくる
０１１０(6)：メモリに数値をおいてくる
０１１１(5)：ある条件が成立したら、直後ではなく別の指示を実行する
　：

のように、ゼロイチの組み合わせですべき処理の内容を決めておきます。 もちろん、こんなに簡単ではありません。なぜなら、「なにとなにを足すか」といった対象も指示しないといけないためです。
ただ、アイデアとしては、すべてにゼロイチ（数字）を割り当てて、それをメモリに置いておいて、その通りに働かせるわけです。

俗に「プログラム」とか「ソフト」と呼ばれているものは、本質的にはこのゼロイチの列からなる手順のセットのことです。
ただし、このままではとてもですが人間が指示するときにしんどいので、もっとわかりやすい形で指示を出します。
ある意味、電卓は指示が直接的に計算に結びつきます。
表計算ソフトは打ち込んだ「数式というデータ」を「表計算ソフトという手順を処理部が解釈することで処理して」、「計算された結果」を見せているわけです。
そして、プログラムを作るという場合のプログラムと呼ばれるものは、人間でも理解できる形で処理を順番に書いていき、それを予め／その場で処理部が直接理解できる形に翻訳する（のも、そういう手順＝ソフトによる）ことで、思った通りに仕事をさせます。

ここまでが、演算処理部とメモリの関係。

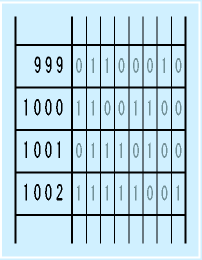メモリは番地で管理

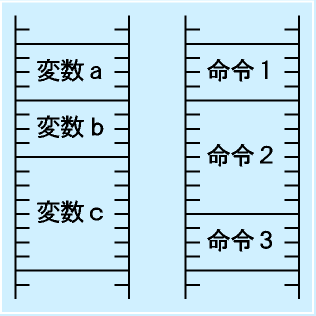必要なバイト数を固めて使う

さて、メモリに手順やデータを置く場合、ちゃんと「どこにおいたか」をわかるようにする必要があります。 そのため、メモリは整然と区画が作られて、それぞれにアドレス（番地）が指定されています。 住所があるから、家々が特定で期す、講義室に部屋番号がついているから、どの部屋かが区別できる、ようなものです。

メモリは、普通は、先ほどの「ゼロイチ」を８個まとめたものをひとまとまりとして扱います。 このゼロイチ１個を「ビット」、８個まとめたものを「バイト」と呼んでいます。 昔からゲーム機本体で「○○ビット」といっていたのは、演算処理部が主に何ビットで作られた数値を扱えるかを意味します。 さすカセットなどで「メガビット」とかいっているのは、その中にメモリが「ビットで数えて」どれだけいっぱい入っているかを示します。今時は「メガバイト」＝「約１００万バイト」単位で数えますが。 いずれにせよ、大きい方が計算力があり（九九だけしかできないか、二桁のかけ算の暗算ができるか、のような違い）、大きい方が情報がいっぱい入っています。

８ビットでひと単位になっているので、大きな数字を表したり、細かな小数を扱いたいときなどは、４バイト分、８バイト分などをセットとして、文章や画像といったさらに大きなものを扱うときはより大量にひとまとまりにして使いますが、
　　アドレス○○○○のところ（から××バイト）においたデータ という形で扱います。
※数値の場合はセット数が決まっているので長さは気になりませんが、文章などは、どこか別のところに「長さ」を書いておくか、おしまいに「終わりです」という印を書いておく必要があります。

ちょっと長くなりましたが、まとめると

1. 演算処理部は「次の処理アドレス」のメモリから指示をもってくる
2. 指示を元に処理する。その際、データが必要なら、どこかのアドレスからデータをもってくるが、そのアドレスは「指示に含まれている」。
3. 「処理アドレス」を一つすすめ１に戻る
4. 場合によっては処理アドレスを別のところに変えることで、処理を変える

という動作をします。

大事なことは、処理手順の指示も、数値も、すべて「ゼロイチ」のセットで、それはメモリ上においてある、それをどう解釈するかはそのときの手順次第、ということです。

※なので、間違うと、本来数値のところを処理として実行しようとして大パニックとか、本来処理手順がおいてある大事なところに数値をうっかりおいてしまって大暴走とかを起こします。 それを未然に防ぐと「不正な処理をしました」っていうエラーが画面にでます。 ので、あれは「不幸なことになる前に止めることに成功しました」っていうメッセージです。

変数

以下の説明を簡単にする意味でも、「変数」という概念を導入します。

といっても、とくに目新しいものではなく、よく、数式などでつかう "x", "y", "t" などの変数、いわゆる「文字」です。 数学では、最終的にこれらの文字に具体的な数字が入るように（最後まで入れない場合もありますが）、プログラムでも、数値などを扱うための入れ物として、「変数」があります。

コンピュータに指示を出すときは、この「変数」に「なにか」を次々代入していくことで処理を進めます。 その「なにか」はどこかからもってきたデータかもしれませんし、複数の変数を計算した結果かもしれません。

で、この「変数」は普通はメモリの上に置かれます。
より具体的には、メモリのとある番地に「変数の名前」をつけて管理し、ある変数が必要になったらその番地のデータをもってくることになります。

＝(イコール)

これまでの算数、数学で、「＝」の使い道は、大きく二つあったと思います。

• 電卓や、計算問題などでみられる
  　　１＋１＝　　（２）
  といった、「答えをだします」「答えは次の通りです」という意味の「＝」
• 数式、方程式などでみられる
  　　
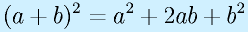
  といった、「右辺と左辺の内容は常に等しい」という意味の「＝」

本質的には「＝」であることにどちらも変わりありませんが、アクションとしての「＝」と、等しいことを実感するための「＝」の違いです。

コンピュータに指示を出すときには、もう一つの「＝」があります。

• 「変数」＝「なんらかの値」

これは、この指示に処理部が遭遇したときに、「変数」に対して、その値を入れる（代入する）、という意味です。

この使い方も、似た経験はあるとおもいます。
　　ｙ＝ｘ＋２に対して、ｘ＝２の場合のｙの値は？
これをあえてコンピュータにやらせるとすると、
　　ｘ＝２　　＜変数ｘに２を入れる
　　ｙ＝ｘ＋２　　＜変数ｙに「ｘ＋２」を計算して入れる
数学の場合との違いは、処理は順番に進むことを前提にするため、この順序で書かないといけないということです（自動的に順番をチェックしてくれる場合もある、ここではｙの計算にｘが必要だからｘが変わったらｙも計算、みたいな）。
ただ、コンピュータで指示を出すときに使う「＝」の大半は、この「入れる」ためのイコールです。

後に出てきますが、あと一個、「判断の＝」があります。
　　「ａ＝ｂ」　　「ａとｂが等しいかどうか」
たとえば「もし、ａとｂが等しいなら○○する」みたいなときに使います。
ただ、「代入の＝」と紛らわしいため、「＝＝」と区別して書いたりします（Ｃ言語系統の場合）。

手順が重要

問題：
　　１２×１２を求めよ
　　また、
　　１３×１３−１２×１２をもとめよ

この計算、電卓でもあれば簡単にできると思います。
前者については、単純に「１２　×　１２　＝」で。
後者については、やすい電卓や携帯電話の電卓だとたぶん、多少の工夫が必要です （最近の関数電卓はそのまま入力すれば答えがでますが）
でも、できると思います。というか、できない人はこの先すごく困るので、できるようにしてください。

具体的な手順の例として、

1. １２×１２を計算する。
2. それをどこかにメモる（頭の中に覚える、も電卓にとってはメモるの一種）。
3. １３×１３を計算して、そこからメモった１２×１２を引く。

があります。

これはまさに、「電卓が(で)計算できるように、問題から、手順をつくりだした」わけです。

同じことを、プログラムで書くと、

1. a=12*12
2. b=13*13
3. c=b-a

ともかけます（もちろん、普通のプログラムなら、直接c=13*13-12*12とかけますが）。

コンピュータを使う、ということは、「問題から手順をつくりだして」「指示する」ことです。 「手順を作る」方法をしっかり考えられれば、プログラムを作ることすら簡単です。 電卓を簡単に使えるように。

電卓

以下、電卓と表計算とプログラムを比較します。
その前にそれぞれどういうものかよく見ておきましょう。

電卓は、いわば、コンピュータの処理部だけが独立したような存在です。
メモリは使う人の頭の中や、メモ用紙が担当します。
使うときは、メモリであるメモ用紙から値を入れたり、計算したりして、その結果をメモ用紙に書き込みます。その計算手順もまた、頭や、メモ用紙に書いてある数式をもとにします。
高級な電卓は例外として、基本的に、計算手順を覚えさせておくことはできず、毎回、手順を入れていきます。

表計算

　　

	A	B	C	D
1
2		12	=B2*B2	「セル」
3		13	=B3*B3

表計算ソフト（たとえばMicrosoft Excel：エクセル）は、画面が「セル」と呼ばれるマス目で区切られています。
ここにいろいろ書き込んでいきますが、そのセル一つ一つがすべて予め用意された「変数」です。
変数を区別する名前としては、横方向に書かれた「A,B,C,D...」と、縦方向の「1,2,3,4...」を組み合わせ、「Ｂ２」のように指定します（Ｒ２Ｃ３といった、横○番縦○番と両方数字にする表記もある）。

このセルに値を書き込むことが「代入」になります。
また、このセルに「＝数式」と書き込むと、このセルに代入すべき値の計算式を指定できます。
右の例では、「C2のセルには左隣のB2の２乗をいれる」と記されています。
表計算では、数式がどこのセルの値を使うかを常に監視していて、使われているセル、たとえば、B2が修正されたら、自動的に計算し直して、C2の値とします。

縦横になっているのは、昔から、縦横の表がよく使われていた、というか、紙の上で表を作るのと画面の上で表を作るのは変わらないので、といったところです。
実験データを整理するときなどは、もともと紙の上の表に値を書き込み、そこをメモ代わりに電卓で計算しましたが、それをパソコンの上でできるようにしたもの、といえます。

もう一つ便利な機能は「グラフでみせる」ことです。これを「データの可視化」といいます。 数字だけではつかみにくい特徴を一目見てわかるようにするといういみで「見えるようにする＝可視　化」です。
一般に表計算ソフトは大量のグラフの形式をもっていますが、工学部のデータ処理で主に使うのは「散布図」くらいです。

プログラム

プログラムは、「プログラミング言語」と呼ばれるもので、いちいち手順を書きます。 手順を書き込んでいくという意味では、電卓よりは表計算に近い存在です。 ただ、表計算ほど「つかい始める」ことが手軽ではなく、表計算ですむなら、表計算ですませた方が楽です。 それでもプログラムを作る意義となる利点があります。

大きな特徴は「判断」が非常にしやすいことです。
たとえば、ある計算を１０回繰り返すとしましょう。 表計算では同じ式を１０回書くことになります（それでも数式のコピーができるので普通は一瞬）。それに対して、プログラムでは、

1. 変数ａに０を入れる（ａ＝０）
2. 数式を計算＜やりたいこと
3. 変数ａに１加える（ａ＝ａ＋１）
4. 変数ａが１０未満なら手順１にもどる、１０ならおしまい（ｉｆ（ａ＝１０）　）

と書きます（もちろん、数式を１０回書いても動きますが）。

ここで「やっぱり１００回」といったときに、表計算は式を１００本にする一方で、プログラムは最後の「１０」を「１００」にするだけです。 また、「いいかんじだから１００万回やって」といわれたら、表計算はお手上げ、プログラムはゼロを追加するだけです。
また、「計算結果が○○だったら終わりにする」といったこともできますが、表計算では適当に多く計算させて、目で見て終わりを探す、などが普通です。

このように、「判断」「条件」「繰り返し」がでてくると、プログラムのほうが圧倒的に「指示しやすく」なります。

加えて、一般にプログラムを作った方が、表計算よりも圧倒的に計算速度が速くなります。 表計算ソフトが「数式を解釈しながら計算」するのに対して、多くのプログラミング言語では、プログラムとして実行する前に「コンピュータが直接わかる手順」に翻訳しておいて、実行するためです。
また、ロボットを動かす場合などはロボットと信号のやりとりをする必要があり、表計算ソフトそのものでは無理です。
一方、プログラミング言語で画面に結果をグラフで表示したりすることは、表計算ソフトに比べればかなり面倒です。

比較

「道具は使い分ける」ことが、重要だといえます。

ある単純な計算を一回するだけの時、わざわざパソコンを動かして表計算ソフトを使ったり、プログラムをつくることはバカらしく、電卓を使うのが当然です。

数回〜数百回（数千回）と同じ計算をひたすらやるような場合は表計算ソフトが向いています。 データさえあれば、あとは数式をコピーするだけですみます。
結果をグラフで見たい、という場合も表計算が便利です。
また、単発の計算であっても、途中経過が複雑だったり、あとでどう計算したかを確認したいという場合は、数式がはっきり残る表計算ソフトが便利です。 電卓では式の間違いに気づいたら全部やり直し、表計算なら数式は残ってますので。

ただ、判断しながら複雑な計算をするような場合は、プログラムを作った方が圧倒的に楽です。 その「楽さ」を体験してもらい、そういう手段があるということを知ってもらうこと、これがこの講義の目的です。