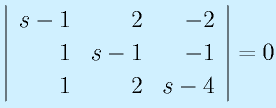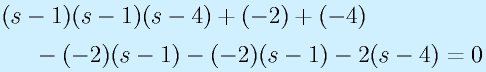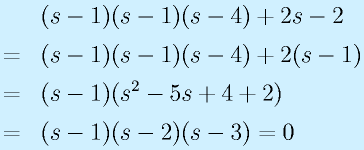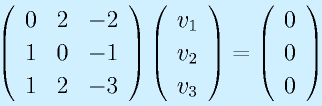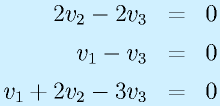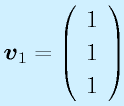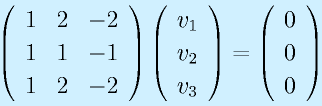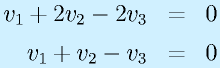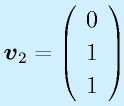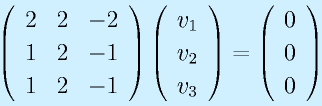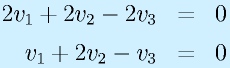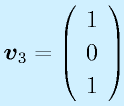制御工学IIでは、ベクトル、行列を多用します(というか、その上に成り立っている理論)。
本来、すでに習っているはずですが、忘れているとこの先の話が混乱しますので、しっかり復習しておきましょう。
(これまで単位を落した人の最大の原因は計算できないことだったり)
ベクトル
ベクトル:
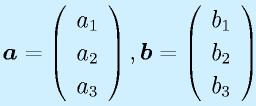
標準で縦ベクトル、一般に小文字、ボールド(太文字)表記
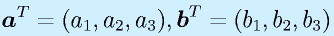
転置(T)で横ベクトル。
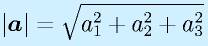
ベクトルの長さ(大きさ)。
用途:
ベクトルは状態変数など、状態量をあらわすのに使用。
ベクトルの加算、スカラ倍:
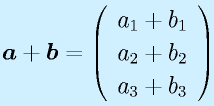
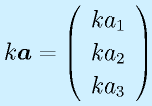

ベクトルの内積:
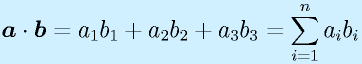
ベクトルの内積はその平行具合いを示します。2、3次元では成す角度をθとして、
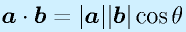
となります。定義から、
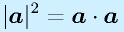
であるため、状態量の大きさ評価として用いられる場合もあります。また、

と行列の積として書くことがあります。
行列
行列:
例)
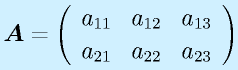 、
、
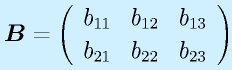
(2×3)
行列は数字や関数を縦m行×横n列の形に並べたものです。
一般に大文字、ボールド表記。
特にm=nの場合、n次正方行列といいます。
ベクトルは行列の特殊な例(n×1、1×m)とも見ることができます(行列とベクトルの演算は行列同士の演算として扱える)。
各成分を個別に扱うときには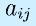 の形で第i行第j列を表します(小文字、非ボールド、添字)。
の形で第i行第j列を表します(小文字、非ボールド、添字)。
用途:
行列はシステムを表したり、システムを評価したり、値の重要度を重み付けしたり、この科目では非常に多用されます。使えるようにしましょう。
行列の基本演算:
行列の和は行の数および列の数が等しい行列間のみで定義できます。
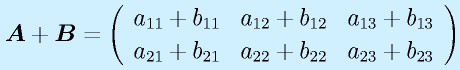
スカラ倍は各要素がスカラ倍になります。
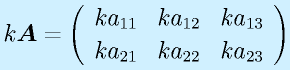
行列の積:
行列の積は、行列がl×mとm×nの形と、一つ目の行と二つ目の列の数が一致するときのみ定義でき、l×nの行列が出来ます(もちろん l=m=n という場合もあり)。
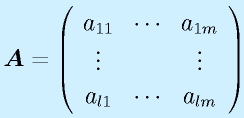
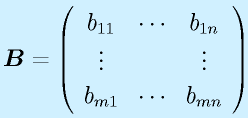
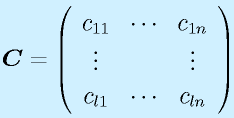
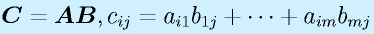
定義は上式のようになりますが、覚えるときは以下のようなイメージで覚えると分かりやすいかもしれません。
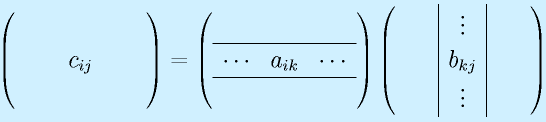
注意:
一般に、
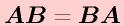 は成立しない
は成立しない
ことに注意。そのため、行列の乗算を行うときは、「右からかける」「左からかける」と掛け方に注意します。
例)
 に対して
に対して
左からCをかけた と、右からCをかけた
と、右からCをかけた は成立しますが、
は成立しますが、
左右をごちゃまぜした は一般に成立しません。
は一般に成立しません。
行列によるベクトルの変換:
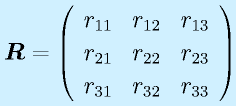
、
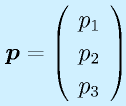
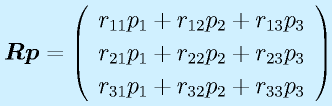
たとえば、3次のベクトルに左から3×3の行列をかけると、再び3次のベクトルになります。
行列の形
転置:
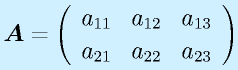
に対して、
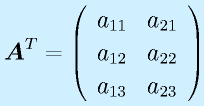
と行と列を入れ替えたものを転置と言い、右肩に添字Tをつけて表します。
("Tenchi"のTではなく、"Transpose"のT)
行列の積の転置については以下の式が成り立ちます。
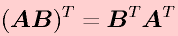
行列の積の転置は個々の行列の転置を逆順にして乗じたものです。
行列の分解、合成:
m行n列の行列Aに対して、
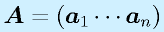
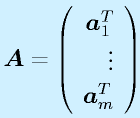
のように、縦ベクトル、横ベクトルに分割して考えることがあります。それぞれ、列ベクトル、行ベクトルといいます。
同様に、

のように行列を並べて行列を作ったり(縦線を引く場合と引かない場合とありますが書き方が違うだけ)、
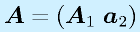
のように、行列とベクトルをセットにして行列にすることもあります。
また、
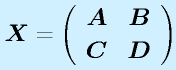
のように縦横に組むこともあります。
行列式
行列式は正方行列から以下の式で計算する数値です。大きさそのものではありませんが、いろいろと多用される数値です。
表記:
行列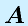 に対して、
に対して、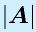
計算:
2次正方行列:
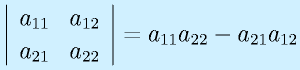
3次正方行列:
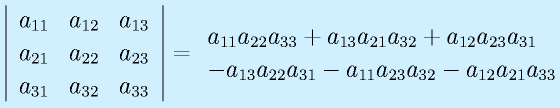
行列式には以下の性質があります。
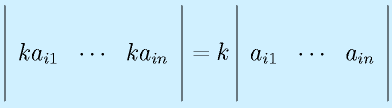
ある行の要素すべてに共通の因子がある場合、それをくくりだせる。
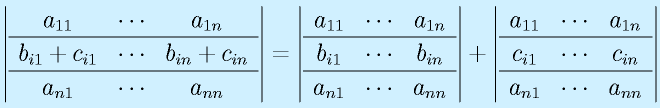
※ただし、3つの行列でi行以外は共通。
ある行に注目して、二つの行列式の和に分解できる。
- 二つの行を交換すると、行列式の値は×(-1)。
- 二つの行が等しい行列の行列式は0。
- ある行に、任意の定数をかけて、他の行に加えても、行列式の値はかわらない。
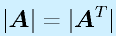
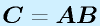 なら
なら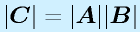 。
。
以上のルールは列に対しても成立。
行列式と余因子
n次の正方行列A
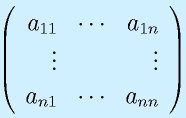
から、i行とj列を抜きます。
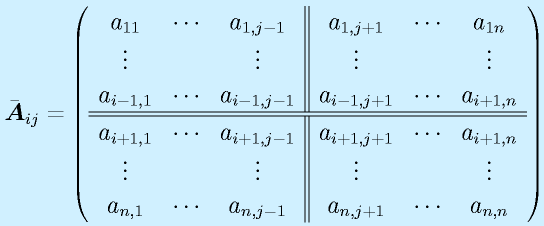
これに対して、行列式を求めて、符合をつけた
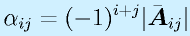
を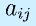 に対する余因子といいます。
に対する余因子といいます。
この余因子を使うと、より高次の行列式を計算できます。
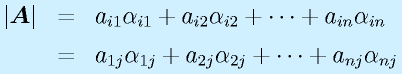
逆行列
n次正方行列Aに対して、
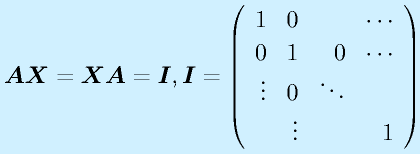
(行列Iは対角成分のみ1で残りは0のn次正方行列、単位行列、Eと表記することも多い)
となるようなn次正方行列Xを、Aの逆行列といい、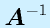 と右肩に"-1"をつけて表します。
逆行列は必ず存在するとはかぎりません(行列式が0でない場合に存在)。
と右肩に"-1"をつけて表します。
逆行列は必ず存在するとはかぎりません(行列式が0でない場合に存在)。
計算:
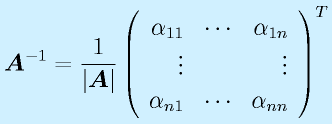
で求めます。全要素に対する余因子を計算して、ならべて行列にして、転置して、行列式で割る、です。
性質:
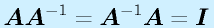
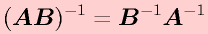
「積の逆行列」は個々の行列の逆行列の逆順の積」になります。(c.f.転置)
逆行列は、「行列の逆数」「行列分の1」的な扱いが可能であるため、今後の制御理論の式変形などで多用されます。
階数(rank)
行列の各行、各列が互いにどのくらい独立しているかを表す数値として階数(rank)という数値があります。
現代制御理論では、「可制御」「可観測」という、制御できるか、状態を把握できるかを分析するときに使用します。
階数を求めるには、以下の基本変形を行います。
- ある行(列)に0ではないスカラをかける
- ある行(列)に他の行(列)のスカラ倍を加える
※行に対しては行、列に対しては列
- 二つの行(列)を交換する
この操作を繰り返すことによって、
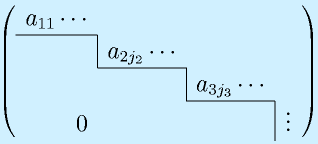
という階段状に変形できます。このとき、
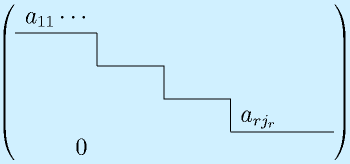
のように、r行までで止まって、r+1行以降が0になったとき、このrを階数、rank といいます。
もちろん、0の行が現れなければ、行列の行数がrankになります。
固有値、固有ベクトル
ベクトル x を行列 A で変換するとき、

(行列 A にかけても、λ倍になるだけ=方向変わらず)
を満たす、0ではない x を固有ベクトル、λを固有値といいます。
定義より、
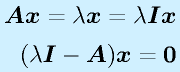
が成り立ちます。ここで x が0以外の値をとるためには、
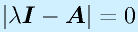
となる必要があります。
※この行列式が0でなければ逆行列が存在し、
※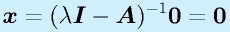
※となってしまうため。
この方程式、
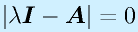
を特性方程式と呼びます。なお、

ならば、

も成立します。固有ベクトルの大きさは定まらず、各要素の比率(ベクトルの方向)のみ定まります。
また、特性方程式はλのn次方程式になるため、重解がなければ固有値、固有ベクトルはn組あります。
重解の場合、対応する固有ベクトルはn本得られることもありますが、足りなくなる場合もあります。
行列の対角化
固有値λ1…λnに対応する、固有ベクトルをv1…vnとします(重解の時はn本求まった場合)。
ここで、このベクトルを並べてできる行列
![\vect{T}=[\vect{v}_1~~\vect{v}_2~\cdots~\vect{v}_n]](eqn/math.bhtml.eqn310.gif)
を考えます。
![\vect{AT}&=&\vect{A}[\vect{v}_1~\cdots~\vect{v}_n]\nonumber\\&=&[\vect{Av}_1~\cdots~\vect{Av}_n]\nonumber\\&=&[\lambda_1\vect{v}_1~\cdots~\lambda_n\vect{v}_n]\nonumber\\&=&[\vect{v}_1~\cdots~\vect{v}_n]\Mss{\lambda_1}{}{0}{}{\ddots}{}{0}{}{\lambda_n}\nonumber\\&=&\vect{T}\Mss{\lambda_1}{}{0}{}{\ddots}{}{0}{}{\lambda_n}](eqn/math.bhtml.eqn311.gif)
左からTの逆行列をかけて、
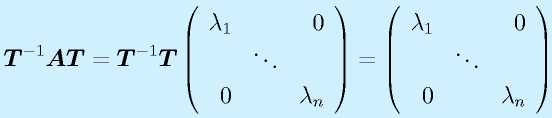
を得ます。つまり、固有ベクトルを並べて作った行列とその逆行列で、行列をサンドイッチすると、対角線上に固有値が並んだ対角行列を得ることができます。
補足:
![&&[\vect{v}_1~\cdots~\vect{v}_n]\Mss{\lambda_1}{}{0}{}{\ddots}{}{0}{}{\lambda_n}\nonumber\\&=&[\vect{v}_1\lambda_1+\vect{v}_2\cdot0+\cdots\vect{v}_n\cdot0,~~~\vect{v}_1\cdot0+\vect{v}_2\lambda_2+\cdots\vect{v}_n\cdot0,\nonumber\\&&~~~~~ \vect{v}_1\cdot0+\vect{v}_2\cdot0+\cdots\vect{v}_n\lambda_n]\nonumber\\&=&[\vect{v}_1\lambda_1~~\vect{v}_2\lambda_2~\cdots~\vect{v}_n\lambda_n]](eqn/math.bhtml.eqn313.gif)
![]()
![]()
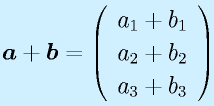
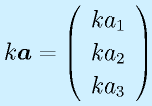
![]()
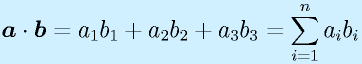
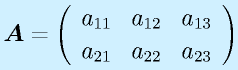 、
、
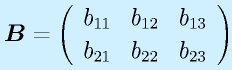
![]() の形で第i行第j列を表します(小文字、非ボールド、添字)。
の形で第i行第j列を表します(小文字、非ボールド、添字)。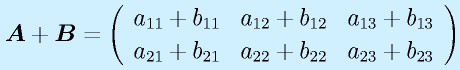
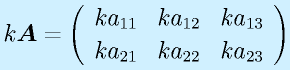

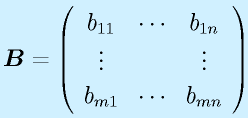
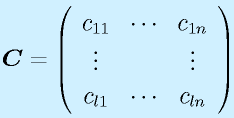
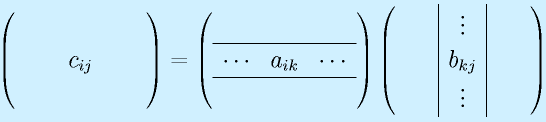
![]() は成立しない
は成立しない![]() に対して
に対して![]() と、右からCをかけた
と、右からCをかけた![]() は成立しますが、
は成立しますが、![]() は一般に成立しません。
は一般に成立しません。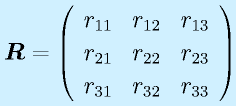 、
、
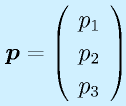
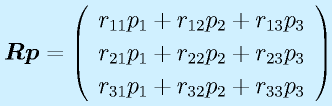
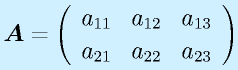
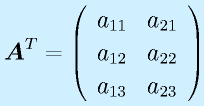
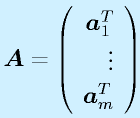
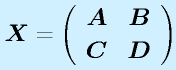
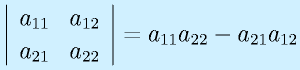
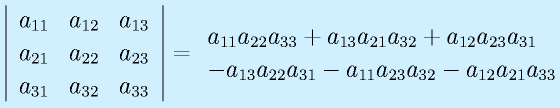
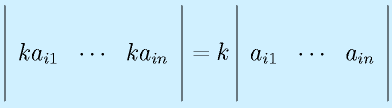
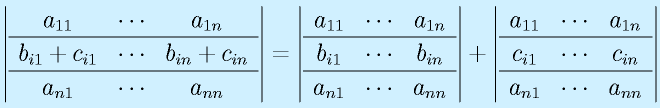
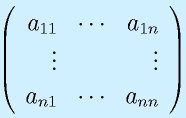
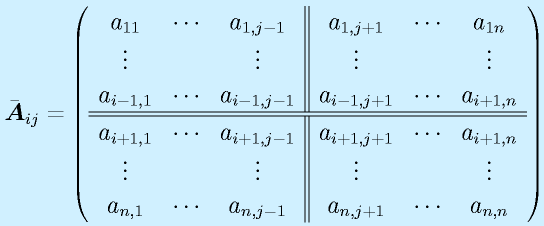
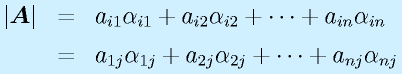
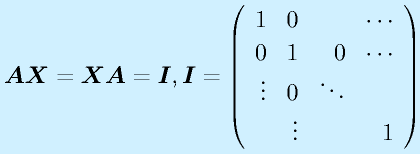
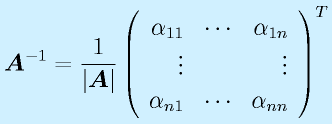
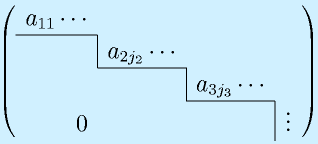
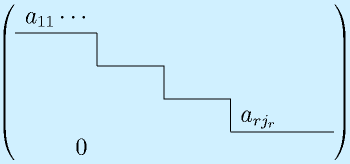
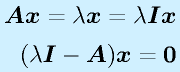
![\vect{AT}&=&\vect{A}[\vect{v}_1~\cdots~\vect{v}_n]\nonumber\\&=&[\vect{Av}_1~\cdots~\vect{Av}_n]\nonumber\\&=&[\lambda_1\vect{v}_1~\cdots~\lambda_n\vect{v}_n]\nonumber\\&=&[\vect{v}_1~\cdots~\vect{v}_n]\Mss{\lambda_1}{}{0}{}{\ddots}{}{0}{}{\lambda_n}\nonumber\\&=&\vect{T}\Mss{\lambda_1}{}{0}{}{\ddots}{}{0}{}{\lambda_n}](eqn/math.bhtml.eqn311.gif)
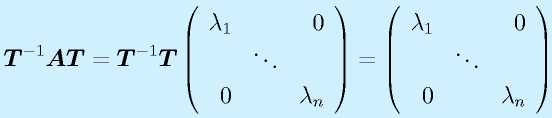
![&&[\vect{v}_1~\cdots~\vect{v}_n]\Mss{\lambda_1}{}{0}{}{\ddots}{}{0}{}{\lambda_n}\nonumber\\&=&[\vect{v}_1\lambda_1+\vect{v}_2\cdot0+\cdots\vect{v}_n\cdot0,~~~\vect{v}_1\cdot0+\vect{v}_2\lambda_2+\cdots\vect{v}_n\cdot0,\nonumber\\&&~~~~~ \vect{v}_1\cdot0+\vect{v}_2\cdot0+\cdots\vect{v}_n\lambda_n]\nonumber\\&=&[\vect{v}_1\lambda_1~~\vect{v}_2\lambda_2~\cdots~\vect{v}_n\lambda_n]](eqn/math.bhtml.eqn313.gif)
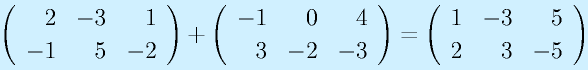
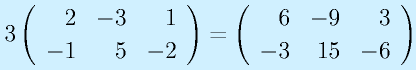
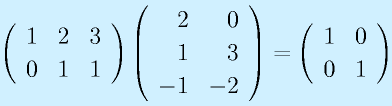
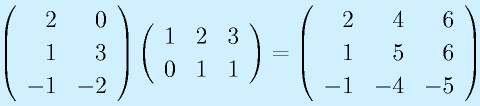
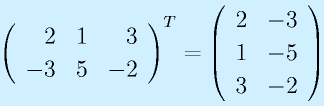
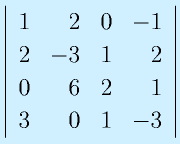
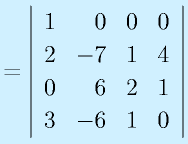
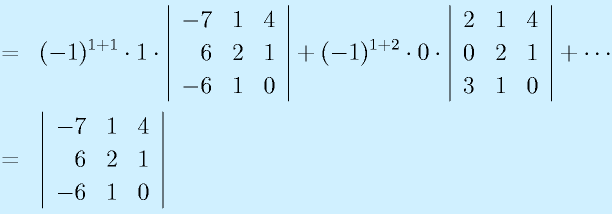
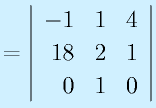
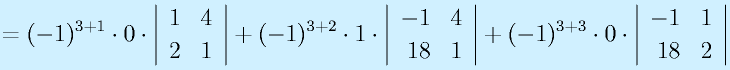
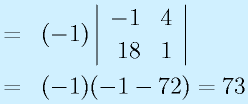
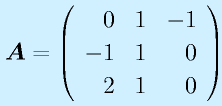
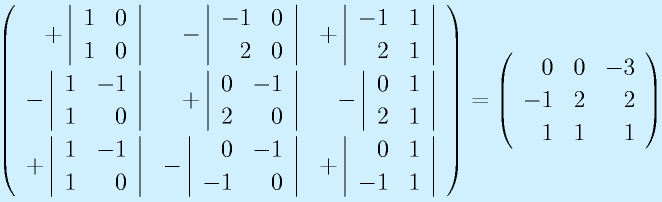
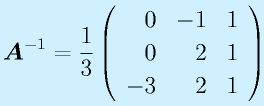
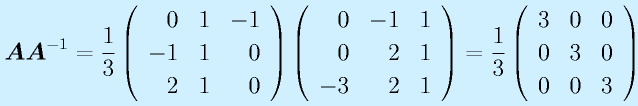
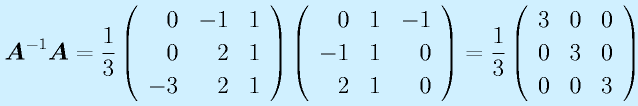
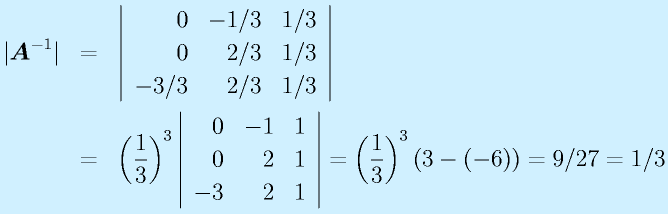
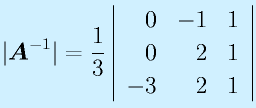
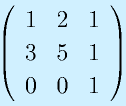 のrankを求めてみる。
のrankを求めてみる。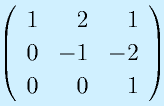
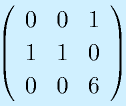 のrankを求めてみる。
のrankを求めてみる。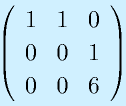
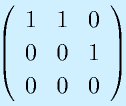
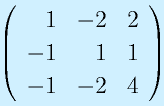 の固有値を求めてみる。
の固有値を求めてみる。