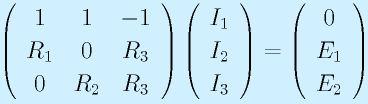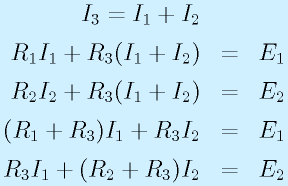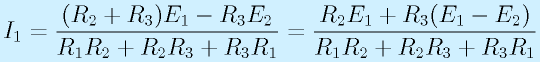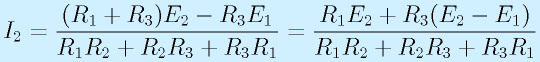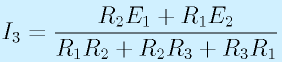電気・電子回路の基礎
[| ]
最終更新: 2018/05/07 10:56:18
B02:メカトロニクスの物理量
概要と到達目標
今回はメカトロニクスにおいて対象となる物理量・状態量のそれを表す単位を扱います。
到達目標:
- 主要な物理量を単位付きで説明できる。
- SI接頭語を使うことができる。
資料アーカイブ 20180416版
物理量
物理量とは、普段我々が工学の理論や計算などにつかっている量です。
たとえば、
- 時間 t[s] 時刻 t[s]
- 位置 x[m] 速度 v[m/s] 加速度 a[m/s2]
- 角度 θ[rad] 角速度ω[rad/s] 角加速度[rad/s2]
- 質量 m[kg] 慣性モーメントI[kgm2]
- 力 f[N] トルク(曲げモーメント) τ・M[Nm] 圧力 p[Pa]
- エネルギー、仕事[J] 仕事率、動力[W]
などの、主に力学的な量と単位は機械工学を扱う上では頻繁に出てくるものです。多くの場合、単位が設定されていて(比率をあらわすもの、例:ひずみは無次元[]という単位です)、それを式中で表すための、暗黙に合意された文字があります。
これらには、位置や速度のように時間と状況によって値の変わる、共に変化することを想定する量と、質量やバネ定数のような変化することを想定しない量があります。
※ロケットのようなものは質量変化も想定、ばね定数も非線形バネや可変剛性機構などは変化を想定しますが全体から見れば一部
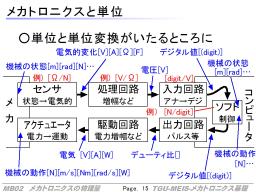
メカトロニクスを扱うには、これらに加えて、主に電気の世界で使われる物理量を合わせて扱う必要があります。また、一つ要素を通るたびに次々に単位が変わっていくことも特徴です(センサやアクチュエータは別形態への変換をするので当然単位も変わる)。
今回は、この物理量について押さえます。
SI単位系
現在、我々が使う単位は「SI単位系」と呼ばれる、単位のセットです。ごく一部の国が独自の単位を使っていますが(数値の変換が必要で迷惑)、世界的には大半がこの単位をメインに使っています。
SI単位系は、主に三つの要素から構成されます。
- 基本単位: 時間[s] 長さ[m] 質量[kg] 電流[A} 温度[K] 物質量[mol] 光度[cd] の7種類の単位。他の単位はすべてこれらの組み合わせで作られる。
- 組立単位: 基本単位を組み合わせることで、他の量を表すための単位としたもの。主に物理法則や定義に従ってつくられる。
例:力:ニュートンの法則 f=ma → 質量[kg]×加速度(位置を時間で2回微分)[m/s2] → [kg m /s2]→[N]
例:圧力:圧力は単位面積当たりの力 → [N]÷[m2] → [N/m2] → [Pa]
- SI接頭語: 大きすぎる値、小さすぎる値を表現しやすくするための桁を調整するための文字。
例:[k:キロ]は1000を表す
ここで興味深いことは、根本的な単位は少なく、その単位を法則などでつなぎ合わせていく、ということです。
いいかえれば、この7基本以外の量は、すべてこの単位だけで書き表すことができます。
※時間変化に関わる、微分は時間で割ること[/s]、積分は時間を掛けること[×s]にあたります。
※たまに、トルク[Nm]と仕事[Nm]のように、別物なのに単位が同じになることがあります。
※角度を表す[rad]は無次元の値(円周「率」、円周と直径の比、[m/m]=[])ですが、「角度であることを表すため」に[rad]と明記される一方で、単位の計算では消えたり湧いたりすることがあります。
※例)円弧の長さ[m]÷半径[m] → [m/m]=[] → 中心角[rad] ※発生
※例)トルク[Nm]×角速度[rad/s] → [Nmrad/s] → 動力[Nm/s] ※消滅
一つ重要なことは、「法則に従って計算すると、単位も自動的に目的のものになる」ということです。
このことを利用すると、なにか計算をしたときに、数値だけでは無く単位も計算していき、それが目的の単位になるかどうかのチェックをすることで、計算間違いや法則の適用間違いを検証する手段となります。
各種計算では必ず単位も確認するようにしましょう。
蛇足:
組立単位は法則によって決まっていますが、基本の7単位だけは、なにか特定の基準があって「こういう大きさを1[m]とする」といった定義がされています。[m]はもともと、地球の北極~赤道の距離を(1万×1000)分の1にした値です(だから、地球一周が約4万[km]になる←地球の大きさが先)が、いまは真空中の光の速さから決めています。速さから長さを決めるためには時間が必要ですが、時間は原子の放射の周期から決めています(いうまでもなく、元は1日→24時間→60分→60秒)。
と、これらも何らかの現象を用いることで、定義づけられているのですが、質量の[kg]だけが「国際キログラム原器」という金属の塊の質量を1[kg]とする、という恐ろしい定義です。ただ、これも設定し直すための検討がされているそうです。
SI単位系の前はMKSA(m-kg-s-A)単位系(MKS単位系)が使われ、CGS(cm-g-s)単位系がありました。「kg重」はMKS時代のもので、いまは[N]のみを使うことに決まっています。
SI接頭語(接頭辞)
数値を扱うときに、小さすぎる値、大きすぎる値が出てくることがあります。
そのときに、ひたすら0を書いて桁をずらさなくてもいいように、「×10の○乗」(しばしば、「×10^○」とも表記されます)を書かなくてもいいように、桁をずらすための接頭語があります。
| 文字 | 読み | 数値 | 使われる対象、備考 |
| k | キロ | 10の3乗=1000倍 | 多くの単位、抵抗値、周波数、電力、電圧 |
| M | メガ(メグ) | 10の6乗=100万倍 | 圧力・応力、動力、抵抗値(その場合のみ「メグオーム」と読む場合がある)、周波数 |
| G | ギガ | 10の9乗=10億倍 | 縦弾性係数、周波数 |
| T | テラ | 10の12乗 | 周波数 |
| m | ミリ | 10のマイナス3乗=1/1000 | 多くの単位、時間、電圧、電流、電力、インダクタンス |
| μ(u) | マイクロ | 10のマイナス6乗=100万分の1 | 長さや体積、電気容量、インダクタンス、時間、電圧、電流、μはギリシア文字で扱いづらいため、uで代替することがある |
| n | ナノ | 10のマイナス9乗 | 電気容量 |
| p | ピコ | 10のマイナス12乗 | 電気容量,時間 |
| 一部の単位と共にのみ用いられる |
| d | デシ | 1/10 | 小学校以来つかっていないデシリットル[dL]、制御などで出てくるデシベル[dB] |
| c | センチ | 1/100 | おなじみセンチメートル(工学では使わないこと!)。輸入物の缶ジュースなどで[cL:センチリットル]という書き方有り |
| h | ヘクト | 100倍 | ヘクトパスカル[hPa]で一躍有名に。面積を表すヘクタールはヘクト+アールなので[ha]。<アールはラテン語の面積(area)かららしい。 |
| da | デカ | 10倍 | 適用例が長いこと見られなかったが、daN(デカニュートン)としての使用が見られる。ほぼ[daN]=[kgf]となるため使われていると推定。 |
| 以下は雑学 |
| K | キロ | 2の10乗=1024倍 | コンピュータの世界(主に容量)でのキロ。大文字。1000を大文字で書かないこと |
| M(Mi) | メガ(メビ) | 2の20乗 | コンピュータの世界でのメガ |
| G(Gi) | ギガ(ギビ) | 2の30乗 | コンピュータの世界でのギガ |
| T(Ti) | テラ(テビ) | 2の40乗 | コンピュータの世界でのテラ |
一般には「10の3乗」単位のものだけを使いますが(センチメートルは使用しないこと)、[dB:デシベル]のように[B]では値が小さすぎることから[dB]で一体化して一つの単位になったようなもの、[hPa:ヘクトパスカル]のように元々使っていた[mbar:ミリバール、天気予報で常用されていた気圧の単位]と数値を変えないで済むように(直感的に比較できる)桁の調整をした場合、ほぼ同パターンですが、従来の[kgf:キログラム重≒9.8N]を使えなくなって値のほぼ近い[daN:デカニュートン]が導入された例、などでは限定的にその他も使われています。ちなみに、[da]は[daN]の前には使用例を見ていません。
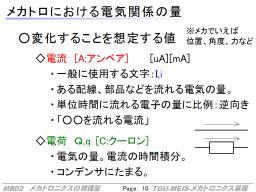
電気関連の物理量
電気に関係する量には以下のような物があります。
| 名称 | よく使われる記号 | 単位 | 説明 | 水の流れによるたとえ |
| 主にその変化・大きさに着目する量 |
| 電圧、電位差 | E,e,V,v | [V] (ボルト) |
電流を流そうとする圧力。 | パイプの両端にかかる圧力の差 |
| 電流 | I,i | [A] (アンペア) |
電気の流れ。細かく見ると電子が単位時間に流れる量(電子の流れる方向と電流の方向は逆) | 水の単位時間の流量 |
| 電荷 | Q,q | [C] (クーロン) |
電子のまとまった量としての、電気の量。電流の時間積分 | 水の体積 |
| 電力 | P | [W] (ワット) |
ある部品(or回路)に電圧Eがかかっていて、電流Iが流れているとき、P=EI、いわゆる消費電力など | 水が運ぶ動力 |
| 周波数 | f | [Hz] (へルツ) | 周期的な繰り返しがみられる変化の、1秒間あたりの繰り返し回数。 | |
| 主に定数としての値(部品などのもつ特徴) |
| (電気)抵抗 | R | [Ω] (オーム) |
対象に電圧Eがかかって電流Iが流れているとき、R=E/Iで定義される、電流の流れにくさ | パイプの細さ |
| (電気)容量 | C | [F] (ファラッド) |
コンデンサの働きの大きさ?を表す | バケツの底面積 |
| インダクタンス | L,M | [H] (ヘンリー) |
コイルの働きの大きさ?を表す | はずみ車付き水車のはずみ車の大きさ |
| | | | | |
電圧、電流については、これまで漠然と理解している、電圧電流の考え方で十分と思います。
電圧は「差」として定義されているため、
- A点から見たB点の電圧(方向=正負あり)、A点とB点の間の電圧(大きさのみ)
- 部品Cにかかる電圧(2端子ある部品の場合の両方の端子間電圧)
- D点の電圧
という表現があります。基本的に2箇所必要になりますが、三つ目の表現も頻繁に使われます(むしろ最も多い)。これは、電子回路を作る場合には、回路内に電圧ゼロとなるべき基準点(コモン、グランド、アースなど)を定めることが一般的で、ここに対しての回路の各部の電圧をいう場合に使う表現です。
なお、電圧を表す文字にE(e)とV(v)がありますが、特に使用に明確な区別は見られません(VoltageからVを使うのは妥当ながら、単位[V]と同一なのを避ける?)。
同じように、電流は配線や、部品(指定しなければ2端子の部品)を流れる電流という表現になります。
電圧、電流、電荷については、大文字が使われる場合と小文字が使われる場合があります。
大文字が使われることは多いのですが、明確に時間変化を意識する場合、つまりv(t)と書いたり、時間で微積分する場合などには、小文字で書かれることが多く、この科目でもそのような方針とします。
抵抗、容量、インダクタンスの関わる、抵抗器、コンデンサ、コイルについては、今後その性質や法則などをそれぞれ解説します。
法則などが出てくるたび、これらの量の文字、単位にも慣れてください。
SI接頭語を含む場合の計算【重要】
上述のように、単位には接頭語をつけて使うことが多いのですが、これはしばしば計算間違いを起こし、その結果大きく桁違いの計算となり、大変危険です。
そのため、SI接頭語を含む数値で計算するときは、面倒でも「×10の○○乗」型に直してから計算するようにします。
例)
- 10[N]の力が1[mm]×2[mm]の面に作用する:
10[N]÷(1[mm]×2[mm])=10[N]÷(1×10^-3[m] × 2×10^-3[m])=5×10^6[N/m2]=5[MPa]
- 3[mV]×5[mA]=3×10^-3[V]×5×10^-3[A]=15×10^-6[W]=15[uW]
特に後者は、なんとなく両方とも[m]なので、そのまま[mV]×[mA]を[mW]としかねないので要注意です。
蛇足:
機械科の計算間違いは人の命に関わると良く言われます。
機械の計算では、ものの強度に関わる計算がしばしばでてきます。
ここで、もし、本来必要な強度の1/1000と間違ったとしたら、重大な結果を招くことはいうまでもありません。
たまたま、チェックを通り抜けてそのまま物になってしまったとき、すぐに壊れて気付くこともありますが、たまたま大きめの値になっていた場合でもそのうち壊れたり、「普段は動作しないけど、いざと言うときに動作する」ような箇所はそのときがくるまで問題に気付かなかったりと、大きなトラブルになります。普段から「桁の間違い」を起こさないように注意して計算する癖を付ける必要があります。
蛇足の蛇足:上記のmA,mVの計算間違いが原因で60点に届かなかった事例があるような。
関連情報
B03:回路の基本要素と回路図
概要と到達目標
今回からメカトロの主要な部分である電子回路部分の基礎を扱います。今回は回路の要素とその図による記述方法です。
到達目標:
- 主要な要素を説明できる。
- 回路図の基本的な書き方を説明できる。
資料アーカイブ 20180423版
電気・電子回路の基本要素
電気的な特性を持つ部品を配線でつなぎ合わせたものを電気回路、電子回路とよび、メカトロニクスではそれによって、メカに取り付けたセンサの情報をコンピュータに伝え、コンピュータの出力をアクチュエータの駆動につなぎます。技術的にはコンピュータは分けて扱いますが、コンピュータも電子回路であり、メカトロのメカでは無い部分で形のあるもの(ハードウエア)は電子回路といえます。
※[電気]回路と[電子]回路の区別は、一般には後述の能動素子を含むかどうか、という説明が多く見られます。以下では電子回路、で表記します。
電子回路は、様々な要素から構成されますが、大きく分けると三つにグループ分けできます。
- 電源: 回路に電流を流そうとする要素。電力{電圧・電流}を供給する。
- 受動素子: 抵抗やコンデンサなど、電力の消費や蓄積をするもの。能動素子以外全般。
- 能動素子: 増幅や整流という作用をもつ。今日の電子回路においては半導体でつくられる。
※[素子]は[部品]と読み替えてほぼOK
これらの要素は様々な形で、実際のものを構成します。小さ単機能の部品、ある程度部品がまとまって目的の機能を持つようにしたモジュール(電子回路基板などもモジュール)、これを単独で動作するようにした装置、などです。
上記のうち、受動素子と能動素子は部品レベルであることに対して、電源だけは電池のような部品レベルのものから、発電所のような大規模システムまで様々あります。
(受動素子については、箱に収めた巨大な抵抗、電力用に用いる大型のコンデンサ、トランスなど、大きな物はあるが、単に大きな部品という解釈はしうる)
一方、様々な解析を行うときには、実際にものが存在しないのに、そこにあることをモデル的、数学的に想定する要素もあります。
たとえば、直流のモータは、(1)線を巻いて電磁石にしたことでもつコイルの性質 (2)その巻いた線などの電気抵抗 (3)回転数に比例して発生する電圧(発電機としての性質) という特徴をもつため、これを電気的に扱おうとしたときには、コイルと抵抗と直流電圧源を直列つなぎにしたようなモデルを考えます。
また、電池は、電圧を発生させるという機能がありますが、電流を多く流すほど外から見た電圧が下がるという性質があります。これを説明するために理想的な電源に抵抗が直列につながっているようなモデルを考えて説明し、この抵抗を内部抵抗といいます。実際に抵抗という部品が入れてあるわけではありません。このようなモデルのことを等価回路と呼び、回路の設計・解析をするときなどに良く用います。
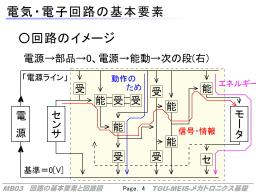
おおざっぱな、回路の構成のイメージを右に示します。
回路には電源から、通常は一定の、電圧が供給されます。回路の主な目的機能を担う箇所に能動部品があり、その働きを補助するように受動部品が使われます。能動部品を通った信号は次の能動部品につながり、順次伝えられていくことで、最終的な作業につながります。
メカトロにおける回路の目的は、電気信号、つまり電圧や電流の変化の形で、情報を伝えることです。
つまり、センサにより得られる電気的な変化を調整してコンピュータに伝え、コンピュータからの信号を大きな電力に直してアクチュエータの動力源にします。
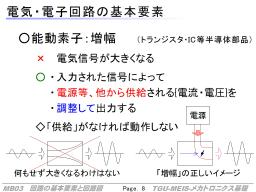
この中で最も重要な働きが、増幅です。
増幅とは、見た目の変化では「信号の幅を増やす」ことですが、元の信号が単に引き延ばされて大きくなるわけではありません。
増幅機能をもった部品には必ず電源からの電力の供給があって、入力された信号によってこの量を調整して、出力します。
出力されるのは、大きくなった入力ではなく、入力によって調整された別のもの、です。
実際、増幅する部品において、入力の電気が出力に混ざるものもあれば、入力の電気が出力にはまったくでてこないものもあります。
さて、先ほどの回路のイメージ図を改めてみてみましょう。
よく見ると、能動部品は電源からくる上の線(一般に電源ラインと呼ばれる)からの供給があります。ものによっては、電源に返すための下の線につながっています。
そこに、左の方から来た信号が入力され、この増幅という[入力で電源から出力への流れを調整する動作]が行われます。
これを次の能動部品に入力し、増幅などをしながら順に右に送っていきます。
ただし、この能動部品は、動作に様々な制約や癖があるため、ちゃんと動作させるために周りに受動部品を必要とする場合があります。
また、増幅動作の前提として、次の段に送るだけではなく、信号とは別に上から下に電流を流さなければ動作しないことも多くあります。
そのため、各所で、伝えるべき情報は左から右に、動作のために必要な電流が上から下に(上から右の下に)流れていきます。
最後のアクチュエータに流す電流は動作のために必要な、エネルギーとしての電気ですが、その途中でも電流が流れます。
※多くの回路の「消費電力」はこれで、たとえばスマホは「画面を光らせる、音を出す、電波を飛ばす」という対外的な電気の消費のほかに、各種演算などをするために、このような「上から下に流れる電気」が消費されています。
回路図
回路を説明したり設計するときに使う図に回路図があります。
機械の設計では機械製図がありますが、機械製図と回路図はかなり方針が異なります。
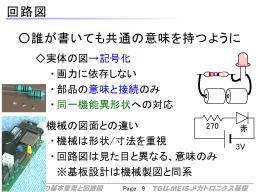
機械製図では、各部品などを「見える形そのもの」で書きます。
一方、回路図は、抽象化し、どのような機能の部品をならべてどう接続するか、を記号によって書いたものです。
そのため、回路図と実物は、機能的にはほぼ一致しますが(理想と現実の差はある)、見た目は全く異なります。
右図の右の接続図のうち、上のものは作ろうとする回路を、部品そのものの形でイラスト化しています。
乾電池2本、抵抗とLEDです。このような図のことを実体配線図といいますが、LEDを光らせたい、という目的だけなら、電池は単1でも単3でもほぼ変わりませんし、最初から3Vくらいの電池でもいいわけです。抵抗も図のような足の生えた大きな部品でも、チップ部品という米粒よりも小さいような部品でも同じように機能します。
そのように、機械の部品と違って、電子部品は「同じ機能を持つ」部品が様々な種類で存在します。
そのため、「回路の設計」という段階では、ひとまず具体的にどんな部品を使うかは抜きにして、どのような機能の部品を使うかだけを考えます。
その結果を書き表す図が回路図で、右下のような形になります。
そのため、電子回路を扱うにあたっては、「どの機能をどの記号で書くか」を知る必要があります。
以下では、回路の要素と共に、その記号を示していきます。
なお、機械にも回路図にあたるような抽象的な段階の図はあり得ます。機械の機能を検討するとき、たとえば、モータから減速比をどれだけにして、どのような機構をつかって、という段階です。
しかし、この段階の図が最終的な設計結果として出てくることはあまりありません。それをもとに実際の部品図や組み立て図までいって設計の成果になります。
また、配管のつなぎ方の構成は回路と似ており、その図は回路図に似たような特徴を持ちます。
反対に、電子回路でも実際に回路を製造する段階ではプリント基板の設計が必要となり、これは実在の部品を選定した上でその寸法に基づいて並べ、太さを考えながら配線をしていきます。これは機械製図と同じ段階にあたります。
ただし、一般には「回路の設計」と「基板の設計」は明確に担当が分かれていて、回路図が最終的な設計成果となる場合も一般的です。
また、専用の基板を起こさずに、回路図から直接部品を組み立てていく場合もあります。
その意味で、メインに使う設計図が、「実体をそのまま書く機械製図」と「機能的な意味を書く電子回路の回路図」という違いになります。
ちなみに、回路図を書くときは、電流などの流れの方向を意識します。
具体的には、図の中で、電流の流れる方向が、上から下、左から右となるように、また信号(情報)の流れがなるべく左から右になるように、図を書く慣例があります。機械製図が見た通りを書くために動力の伝達方向などを気にしないことに対して、抽象的であるがゆえ、並べ方が調整できるわけです。
※ある意味、機械製図でも側面図を書くときに、装置の上は図の上に書くので(重力の方向が下)、また上面図を書くときには「手前」を図の下に書く傾向があるように、向きはあります。また、回路図から実物を作るときにも、一般には回路の流れに従って部品を配置していくので、ある程度関係はあります(そのほうが配線がしやすい、電気的な性能に影響)。
回路の要素と記号
電源は前述の通り、主に回路に電流を流して機能させるもとになります。
この電源は、主に何を出力するように意図されたかによって、分類されます。
- 電圧源: 主に電圧を制御・調整している電源。
- 電流源: 主に電流を制御・調整している電源。
いずれも、たとえば、一定の電圧・電流を出力するようにしているもの、または何らかの指示によって指定された電圧、電流が出力できるようにしているものです。電池のように、本質的にほぼ一定の電圧になるものもあります。
電源装置では、「指定された電圧になる」+「指定された電流上限になると{停止する・電圧が下がって電流が減らされる}」という保護付きのものが多くありますが、この場合は一般には電圧源として考えられます(敢えて電流リミットに引っかけると電流源としての性質になるが)。
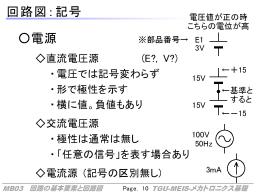
- 直流電源: 極性の変わらない、ほぼ一定の電圧を出力することを意図した・性質のある電源。
- 交流電源: 一定の周期(周波数)で、正負に変化する出力をする電源。正弦波が出るもの、矩形状に上下するものがある。
電源はこの組み合わせで、「直流電圧源」(電池を含む、一般的に電子回路の動作に用意される電源)、「直流電流源」(一定の電流を流すことで機能する部品や回路を動作させるための電源)、「交流電圧源」(たとえば、無停電電源装置は停電時に蓄電池に蓄えた電気から交流100Vを作って供給。発電所の発電機も交流電圧源と解釈できる)、「交流電流源」(交流で動作するモータを本気で制御するときは、モータに流れる電流を制御して供給する。ベクトルインバータ装置など)となります。
なお、一般に「直流」というと電圧・電流が「ほぼ一定」という解釈になりますが、極性が正のままで波打つように変化する電気を「脈流」と呼びます。
これを意図的に出す電源はあまりない(交流を直流に直す過程で生じる)のですが、電源としてみた場合には直流電源が対応できます。
これらを表す記号は右図のようになります。直流電圧源は見慣れた「電池」の記号ですが、1個で任意の電圧を表すため、複数を書き重ねる必要はありません(横に電圧を書く)。交流電圧源の記号は、回路の説明をするときに「任意の電圧波形」を表すのに使われることもあります(特に「負もあり得ます」という意図を込めて)。
以下も含めて、記号にはいくつかの記述が付いてくることがあります。
一つ目は「番号」を表すもので、一般的には、「ジャンルを表す文字」と「数字」で記載されます。電源の場合は「V」や「E」が用いられます。
これによって、説明したりするときに「どの要素か」を特定できます。
二つ目は「性能」を表すものです。電源の場合には、電圧や電流、周波数などが、電池では容量なども記載されます。
これらは必須では無く、全て書かれるとは限りませんが、必要な情報は付記します。
抵抗は「オームの法則」に従って機能する部品で、使い道は様々です。たとえば、
- 電流が流れすぎないように制限するための抵抗(電流制限抵抗)
- ある電圧に対して、流れる電流を決定する
- 電流を電圧に変換する抵抗(電流センサとして使われる場合もある)
- 分圧という方法で電圧を下げるのに使う抵抗(および分流で電流をバイパス)
- 各種回路の中で設計定数を決めるところに使われる(機能は上のもの)
のような使い方があります。
さて、この記号は右図のようなギザギザ記号(左右もしくは上下に3山ずつ)か、長方形記号かのいずれかで書かれますが、一つ微妙な問題があります。
現在のJIS規格では、長方形の記号を使うことになっており、すでに高校までの教育ではこの記号を使うことになっていて、この記号で習っていていると思います。一方で、長方形になるまでの規格はギザギザ記号の方であるとともに、いまだに産業界では広くこのギザギザ記号が使われています(もともと、長方形も記号としてはあったが、ギザギザと微妙に違う意味合いで使われていた)。
この科目では、慣れておくという意味も考えて、実際に使われるギザギザの方をつかいますが、もちろん、長方形記号をつかってもかまいません。
※業界屈指の電子回路雑誌、CQ出版社の「トランジスタ技術」がギザギザを使ううちはギザギザ、と毎年チェックしてます
抵抗は一般に値の変わらない部品(固定抵抗)ですが、意図的に変えられるようにしたものを可変抵抗と呼びます。
単に値が変わるだけなら矢印を書き重ね、抵抗の途中に接点があって、その位置を変えられるようになっている場合は横に矢印をつきたてます。
たとえば、いろいろな出力を調整するための「回すツマミ」には可変抵抗が付いていることが多く(最近はデジタル的なスイッチものも増えた)、角度センサとしても使われています。基板上でドライバで回して調整するようなものもあり、その場合は一度回したら固定してお終い、ということで「半固定抵抗」と呼ばれることもあります。
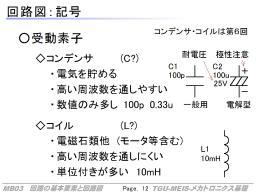
抵抗とならぶ主要な受動部品である、コンデンサとコイルについては、後に改めてその性質を扱います。
一般的な理解としては、コンデンサが電気を貯める性質があること、コイルは電磁石の持つ性質であることを押さえておけばOKです。
コンデンサはその方式にいくつかあり、大きな区分としては、「電解型」か「電解型でないか」があります。電解型は大きめの容量を実現できる一方で、内部に電解液(質)を持っています。そのため、コンデンサの間になにかが入ったような記号が書かれます(これも旧記号ですがいまも見られる:いまは区別しなくなった)。また、電解型の多くは極性を持ち、それを明示する必要があります(+記号をつける、-まで付けないことが多い)。
一方、電解型では無い場合は極性は一般にはありません。
前回の「電圧」のところで説明したように、電圧は基本的に2点で規定するものでありながら、話を簡単にするために、回路内のどこかに共通の基準点を設けて、そこからの電圧で表現することがあります。
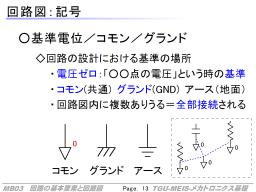
この基準を決める記号が、右のような記号です。
この目的で、現在主に使われているのが、下三角にゼロを付記した「コモン」と呼ばれている記号です。
いまも使われている、以前主流だった線の下に斜線を書いた記号「グランド」(GNDと記載)もあります。
※今でもコモンの記号を書いても「グランド」と呼ぶ場合も見られる
三つ目の「アース」も電位を表す記号の一種ですが、「地球につなぐ」という意味でつかわれる、いわゆる「アース」です。
一般の電子機器の回路図にこれが出てくることはあまりありません(たとえば、スマホはアースしようがない)。
しかし、メカトロ機器の場合には漏電などを防ぐ目的でアースが必須の回路がいろいろとあります。
その意味では一緒に覚えておくべき記号です。
グランドは言葉の意味に地面がありながら地面にはつなぎません。アースは回路の基準電位に使われることも、単にケースそのものだけをアースするという使われ方もありますが、地面につなぐものです。
基準電位である、コモンとグランドは回路内に複数登場することが一般的です。
これは、回路を設計するときには通常、基準電位に対して信号などの電圧が変動することを前提とするため、信号などと基準電位との間に部品が存在することが多いためです。いちいち線を引いてこなくても、このコモン・グランドの記号をかけば、そこが0[V]ですという意味になります。
そのため、回路中に複数あった場合はすべて配線する必要があります。
※実際の回路製作トラブルで一部のコモンの配線を忘れた、とかはあり得て、そのとき全く動作しないのであればいいが、半端にだけ動いて問題発見に手間取ることがある。
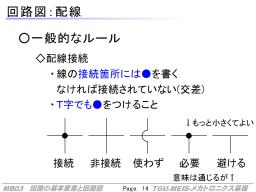
回路を構成するために、各要素の間を線で結びます(普通は垂直水平の直角方向だけで斜め線は使わない)。
これらの線が交わって、接続されるところには●を必ず書きます。
逆に、線が交わっているところは●の有無で意味が大きく変わる(当然回路として動かないどころか事故になることも)ので、●をつけるかどうかは常にしっかり意識するようにしましょう。そのためにも、見れば分かるT字のところであっても、必ず●をつけるようにしましょう。
なお、書き方によっては「乗り越えるような半丸」という表記もありますが、回路設計などではめったに見られません。
基本的なものをいくつか紹介しましたが、これらを頭の中に置きつつ、これから出てくる回路例で慣れるようにすればよいでしょう。
関連情報
B04:オームの法則とキルヒホッフの法則
概要と到達目標
今回は回路の最も基本的な要素である抵抗に関わる法則と、回路内の基本法則を扱います。
到達目標:
- オームの法則を説明できる。
- キルヒホッフの法則について説明できる。
資料アーカイブ 20180507版
回路について考えるための状態量の設定
力学問題を考えるときに対象の座標xを考えたり、流体力学で圧力Pや速度vを流路に沿ってとったりするように、回路を解析するためにも回路内に状態量を設定します。
前述のように、主に変数として、電圧と電流を考えます。
大きく分けると、3パターンあります。
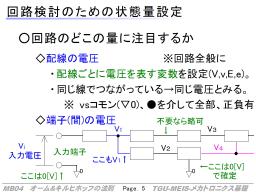
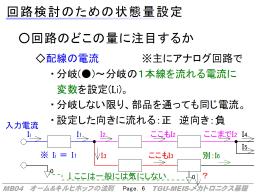
- 配線ごとの電圧:
アナログ回路・デジタル回路(後日)ともに、回路の動作を考える上で、配線がどのような電圧になっているかを設定する。
一般には回路による情報の伝達として、電圧値をつかうことから、その経路上では電圧の関係式として検討することになる。また、回路の動作チェックなどをするときにも、実在の配線の電圧やその時間波形を見ることが一般的である。
この場合の電圧は「回路内の基準▽0に対しての電圧」の表記となる。基準より電位が高ければ正、低ければ負の値となる。
特殊な場合を除くと、部品間をつなぐ線はつながっている限りすべて同じ電圧であると考え、接続(●)を通して接続された線も同じ電圧になると想定する。
一般には、V?, E?, v?(t), e?(t) のように番号(V1)や文字(Vi=V-input, VR=V-Resistorなど)を下付で添えた文字をつかう。時間変化を意識する場合は、小文字(および(t)付き)とし、時間変化にこだわらない場合(=時間変化する場合を含む)は大文字を使うことが多い。
- 配線を流れる電流:
アナログ回路で動作の検討をする場合によく設定される。一方、デジタル回路は配線に流れる電流は僅かで、かつその大きさには意味がないため(電圧の高低を信号につかうため)、電流の状態量を意識することは少ない。
配線が分岐しない限り、間に部品が挟まっていても、同じ大きさの電流が流れると想定する。一方、●で分岐した場合には後述のキルヒホッフの法則で説明されるような関係で、●につながる線ごとに電流は異なる。
そのため、電流は●から●までで一つの変数を割り当て、かつ、●のそばに矢印で方向を明示し、I?,i?(t)の文字にて表記する。
もし、実際の電流が矢印の方向に流れていれば、I,iの値は正となる。逆に、I,iの値が負の場合は、実際には矢印とは反対方向に電流が流れることになる。
これは単に、回路の検討を始めた段階でどちらに矢印を書くかだけの問題ではあるが、「直感的に正の状態(入力電圧が正であるなど)」のときに電流が流れると思われる方向に矢印を向けるべきである(さもなければ、計算してみたら電流が-だらけということになる:現象は間違っていないがフィーリングが良くない)。これから度々出てくる矢印の向きに気をつけるべし。
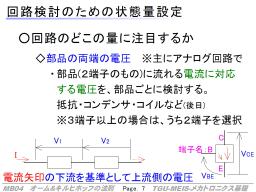
- 部品の両端の電圧・部品に「かかる」電圧:
多くのアナログ回路部品においては、なんらかの「流れる電流と端子間の電圧」の関係を持つことが一般的である。
たとえば抵抗は後述のオームの法則、コンデンサやコイルは電流の積分値や微分値に関連する電圧となる。能動素子でも動作に伴って何らかの端子間電圧を生じることが一般的である(たとえば、青色LEDに電流を流して光らせると、その両端の電圧は3[V]ちょっとになる)。
そのため、部品の両端の配線ごとに電圧を設定する代わりに、部品ごとに両端の電圧を考える場合も多い。
この場合は一般に、まず電流の向きを設定しておき、その電流の矢印に対して、下流側を基準とした上流側の電圧、として、部品の両端の電圧を表す。
部品によっては、これによって「電流が正の時に電圧も正」となる(たとえば抵抗)が、そうとは確定しないもの(たとえばコンデンサやコイル)もある。
能動素子などで3端子以上ある場合も、その説明のために2本を選んで、同じように向きを考えて端子間電圧を見る場合がある。
これらの電圧と電流の設定には「向きがある」ことが重要です。そのため、一般には矢印でその方向を特定し、計算などで得た値の正負と実際の回路の挙動を対応づけることになります。
オームの法則
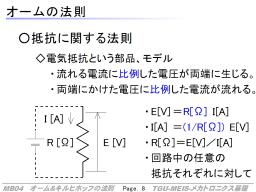
オームの法則は、抵抗に流れる電流と、両端の電圧に関する法則です。
抵抗においては、
- 流れる電流に 比例した 電圧が両端に生じる
- 両端にかけた電圧に 比例した 電流が流れる
という特性があります。これがオームの法則で式で表すと、
![E[V]&=&R[\Omega]\,I[A]\nonumber\\I[A]&=&(1/R[\Omega])E[V]](eqn/basis.bhtml.eqn401.gif)
となります。電圧と電流の比例定数として抵抗[Ω]が使われます。
※もう一方の(1/R)もコンダクタンス[S:ジーメンス]として定義されますが、普段は使わず、(1/R)のままです。
このとき、電圧と電流には当然方向性が有り、上述の「電流の方向に対して、下流側を基準として上流側の電圧」の設定をしていれば、電圧/電流の符号も含めて、抵抗値が正になります。通常のものの抵抗は正であり、ゼロの場合を超伝導といいます。
単体の部品として、抵抗値が負になることはなく、回路の設計などでマイナスの抵抗が必要になったらその時点でアウトです。
※ただし、負の抵抗をシミュレートする回路は存在し、特殊な部品である領域では「電圧が増えると電流が減る」という局所的に負の抵抗のような挙動を持つものもあります。
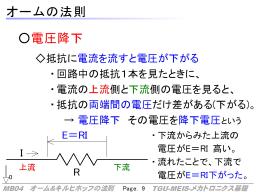
この抵抗を別の観点で見ると、上流側の配線の電圧(対コモン▽0)と下流の配線の電圧を比べたときに、下流側の電圧が下がっています(下流から見て上流がE=RIだけ高いから)。これは、回路に「抵抗をはさんだことで、電圧が下がった」と解釈でき、「電圧が降下した(さがった)」「電圧降下」といいます。
また、この下がった量RIを「降下電圧」(降下した電圧)といいます。
このような「部品を挟んだことで電圧が下がる」現象は他の部品でも見られ、その場合も電圧降下、降下電圧と言われます。
たとえば、LEDが光るときには2[V]~4[V]弱の電圧降下を起こします。
抵抗は本来、電流を制限したり、電流から電圧を生じさせる特性ですが、このことから「電圧を下げる」という機能が説明されることもあります。
また、部品としての抵抗ではない要素でも、この特性を示すようなものに対しては、抵抗としてモデル化することができます。
たとえば、乾電池を含む多くの電池は、電流を多く流すと電圧が低下します。
その電流と電圧の下がり方に直線性がみられ、本来の電圧の直流電圧源のあとに、直列に抵抗が入っている(それによる電圧降下)と想定すると説明をつけられます。これは素材や電極その他による抵抗としての性質が表れたもので、内部抵抗と呼ばれています。
よく「電気をたくさん食うものには単1、少なくていいものは単3」とか「電気を食うものにはアルカリ電池」といった説明がありますが、単3より単1のほうが、またアルカリ電池のほうが、容量が大きいことの他にもこの内部抵抗が低いことも効いています。
ミニ四駆があまり走らなくなった電池でも時計ならまだまだ使えるというのは、電池の消耗で内部抵抗が増加した、と見れば説明ができます。
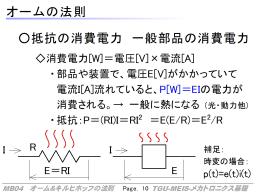
抵抗や部品の消費電力
抵抗に限らず、一般的に部品・その集まったモジュール・装置などに対して、電圧E[V]をかけ、電流I[A}が流れたとき、それの消費電力はP[W]=EIとなります。もし、その部品が外部に何も出力することなく、中に貯めることも無ければ、その電力は熱になって出てきます。
一方、何かをした場合、たとえば、モータの場合は動力[W]を出力しますが、その場合は入力電力と出力の差が熱になります。
電源回路では別の回路への電力供給、照明の場合は光の出力をしますが、その場合も入出力の差が熱になります。蓄電池のような蓄積機能があれば、貯められなかった分(充電すると電池が暖まるのは充電時に貯められずに無駄になった分)。
抵抗の場合は、
![P[W]=EI=(RI)\,I=RI^2~~=E(E/R)=E^2/R](eqn/basis.bhtml.eqn411.gif)
の電力が消費されます。
実際の問題としてこの式をみると、まず、消費は電圧の2乗に比例することがわかります。そのため、電子回路を低電圧で動かすことは省エネにつながり、近年のコンピュータ機器は随分動作電圧をぎりぎりまで下げてきています(※モータなどの場合はエネルギーとして電力を使うのでこの式は直接は当てはまらない)。
一方、電流の2乗にも比例します。たとえば、長い電線で電力を送ろうとするとき、電線のもつ抵抗が無視できなくなります。
このとき、電流を減らせば、電線で消費される電力(単なる無駄、電線による電圧降下分)が減ります。そのため、同じ電力を送るために電圧を高くして電流を下げるという手段が使われます。変電所が必要となりますが、送電線は高い電圧で送ることでこの電力消費を抑えます。
また、大出力のモータなども一般には電圧を高めに設定することで、配線での無駄を減らします。
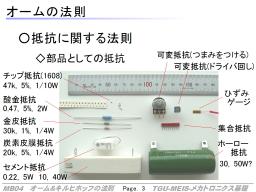
部品としての抵抗
写真は実験室の引き出しから適当にとってきた抵抗です。
記号では1種類ですが、部品としてはいくつも種類があります。
大まかにスペックを記載しましたが、抵抗の種類を変えて変わるのは、精度(表記の抵抗値から最大どのくらいの誤差があるか)と許容損失電力([W]表示)です。
炭素皮膜抵抗は一般的に用いられているものです。
これよりも精度の高い抵抗が必要な場合には金属被膜抵抗(金皮)を用います。抵抗には温度依存性があり、温度によって抵抗値に変化が出ますが、金皮抵抗はその変化も少なく、アナログの演算回路など用いられます。
これらが1/4W (0.25W)程度の電力にしか耐えない(これを超えると嫌な臭いがしたり、色が変わったり焦げたり、極端なときは爆ぜる)のに対して、より大きな電力に耐える必要があるときには、酸化金属被膜抵抗(酸金)やセメント抵抗、ホーロー抵抗などを用います。セメント抵抗やホーロー抵抗はメカトロ系の制御機器などで見かけることがあります。
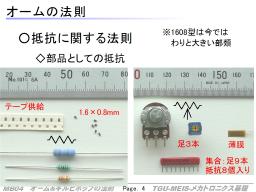
以上の抵抗は足が生えているタイプですが、近年一般化したものにチップ抵抗があります。これは回路基板に貼り付けるように組み付けるもので、小型化が進み、回路そのものの小型化、機器の小型化に貢献しています。
右の方は少し特殊なもので、ツマミを取り付けて、出力調整や設定の入力に使われる可変抵抗、基板上につけて回路の調整などに用いられる可変抵抗(半固定抵抗・ポテンショなどともいわれる)、複数の配線に同時に抵抗を取り付けたいときにつかう集合抵抗など、バリエーションがあります。
ひずみゲージはひずみ(伸び率)のセンサとして有名で、薄いフィルム上に抵抗の膜がジグザグに形成されています。
これを対象となる材に貼り付けると、材の伸縮とともに伸縮し、それによって抵抗値が変わります(伸びると抵抗が増加)。
これによって歪みを測定します。たとえば鋼の引っ張り試験のひずみ計測に使うほか、はりの上下面に貼ることではりにかかる力をえることで、力センサになります。体重計や電子秤の測定部にあります。
キルヒホッフ第1の法則
キルヒホッフの法則は、回路内の電圧と電流の合計に関する法則です。
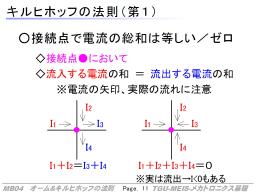
そのうち、第一の法則は回路内の配線の接続点における電流に関する法則です。
平たく言えば、ある接続点(配線の分岐点)に対して「流入する電流の合計と流出する電流の合計は等しい」という非常にシンプルで、当たり前のように思える法則です。
このとき、電流の矢印を意識しますが、実際の電流の向きを考慮せずに指定した矢印の向きでも、符号こみで(実際の電流が矢印と反対向きなら負の値)成立します。
そのため、すべて流入方向(もしくは全て流出方向)に指定した場合は、その合計がゼロになります。現実には、流入する電流があれば流出する電流もあるので、いくつかの電流変数の符号がマイナスになるはずです。
この法則があるため、上記の「配線を流れる電流」での状態変数設定は、分岐点のところで変わることになります。
キルヒホッフ第2の法則
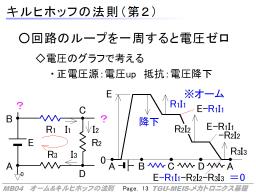
キルヒホッフの第2の法則は、平たく言えば「回路内の任意の輪で、一周回ると電圧がゼロになる」です。
右の例を使って考えます。まず、回路内で部品が配線でつながった適当な輪を確認し、そこに周回方向を設定します(赤の時計回りの矢印)。
その周回に沿って、
- 周回方向に沿って電圧を上げる電圧源はプラス、逆向きならマイナス
- 周回方向と同方向に電流の向きが設定されていれば、RIの電圧降下分を引く、逆向きなら+RIとする(電圧降下の向きが逆になるため)
として一周加算した式を求めると、それがゼロになります。
右の二つ目の図には、電圧の上下をグラフで示しています。
A点を基準とし、A点からスタートし、まず、電圧Eの直流電圧源によって電圧がEだけ上がり(0+E)、B点に来ます。
つぎに、BからCにいく途中には抵抗R1があり、ここの電流がI1流れると置いていれば、R1I1だけ電圧降下を起こします。
よって、B点の電圧はE-R1I1となります。同じようにD点までで-R2I2、A点まででさらに-R3I3です。
その結果、A点からA点までの電圧のアップダウンを合計すると
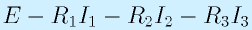
となりますが、同じA点なので、=0となります。
この法則は、部品の両端の電圧を経路に沿って加算していけば、ゼロになるという法則です。
図のB、C、D点には他の部分への配線があり、どれだけ電流が流れるか、この時点では不明です(そのため、C点においてI1とI2で別変数にしてあり、その差が右方向の配線との出入り)。A点も、コモン経由でどれだけ流れるか不明です。
それでも、個々の部分の降下電圧などはわかるため、計算が成立します。
キルヒホッフの法則の適用例
このキルヒホッフの法則による式を連立させると、複雑な回路の電流の流れ方や各部の電圧などを得ることができます。
実際、コイルなどによる微分方程式も含めて連立させて演算することで、回路のシミュレーションもできます。
ここではキルヒホッフの法則に典型的な、例を考えてみましょう。
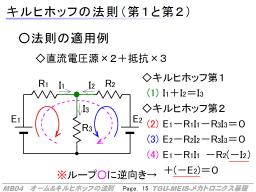
右図のような、直流電圧源が2個、抵抗が3本の状況を考えます。
まず、キルヒホッフ第1の法則によって、
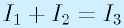 …(1)
…(1)
を得ます。これは上の接続点についてですが、下の接続点でも I3=I1+I2という関係になりますが、これはそのままなので上の式だけで十分です。
次にキルヒホッフ第2の法則によって、
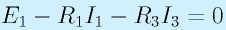 …(2):赤の時計回りループ
…(2):赤の時計回りループ
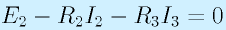 …(3):青の反時計回りループ
…(3):青の反時計回りループ
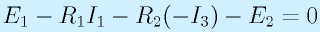 …(4):紫の外周ループ
…(4):紫の外周ループ
の3本の式が得られます。3本目の紫のループの式は、I2がループの矢印と逆向きなので、「ループに沿った電圧降下」にするために電流の向きを逆にし、E2も電圧を下げる方向に入っているのでマイナスにします。
これらを連立させて、E1,E2に対するI1,2,3を求めます。
※I1,2,3に対するE1,E2はキルヒ(2)の式で直接求まりますが、普通は電圧に対して電流がどうなるかを考えます
未知数が3個なので、式3本で連立させます。ここでは、(1)(2)(3)式を用います。
たとえば、
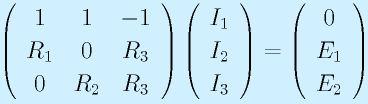
として、クラメルの公式を使って解くことができますし、
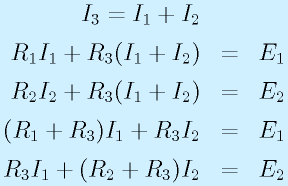
と代入、連立させて、解くのもありです。
結果として、
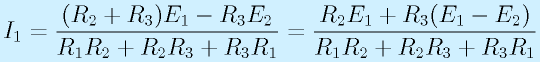
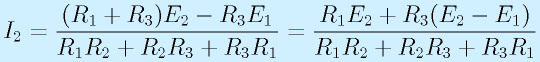
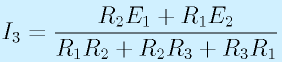
という答えを得ます。
未知変数が3個あるのに対して、式が4本あって冗長になっているのは、キルヒホッフの第2の式が冗長になっているためです(第1も接続点二つ共で式をつくると冗長になるが、さっきすぐに潰したので)。
具体的には、外周を回る(4)の式が、辺々引いた(2)式-(3)式の形になっています。キルヒホッフの第2ではループごとに式を設定できますが、このように隣接するループをセットにしたような式も出てきます。そのためまずは小さな環で式を積み上げるとよいでしょう。
さて、この問題は一般には「例題のための問題」という位置づけになっていますが、これに対応する実在の回路があり得ます。
それは「電源の並列つなぎ」もっと簡単にいえば「電池の並列つなぎ」です。
一般に、電源は理想的な電源と、そのあとに微小な抵抗(内部抵抗)が直列になったものとしてモデル化できます。
つまり、何か対象R3に対して、電源1:E1+R1 と 電源2:E2+R2を並列つなぎにして供給する形の式です。
そう思いながら上の式を見直すと、どんな電源であれE>0ならば、R3には正の電流が流れます(当たり前)。
それに対して、I1, I2については正の電流とは限られないようです。もし、E1とE2が等しければ、R2とR1の比率でI1とI2が決まります。
しかし、R1,R2がR3に対して十分に小さく(それが理想的な電源)、かつ、E1とE2にある程度の差があると、I1,I2の分子の後半のところで、電源電圧の差による電流が流れます。たとえば、E1>E2だと、I2がR3(E2-E1)の分でマイナスになり得ます。
これは実際の電源で考えれば、「正の電圧を出力しようとしたら、逆に電流が流れ込んできた」という状態です。
もし、これが電源装置だとものによったら故障しますし、充電してはいけない乾電池だとそれが原因で液漏れなどが起こりえます。
と、いうわけで、電圧源の並列接続は難しいのです。すっかり同じ電圧特性の乾電池は並列にして問題ありませんが、違う種類の電池を混ぜて並列にすると、この問題が起きるはずです。電源装置も電流が足りないからとうかつに並列するのはやめましょう(並列運転できるものはわざわざその機能が作ってある)。
B05:抵抗の直列・並列と分圧・分流
概要と到達目標
今回は前回の法則などを使いつつ、抵抗の接続によってできる回路の解析をします。
到達目標:
- 合成抵抗の計算をすることができる。
- 分圧の計算ができる。
- 法則の適用方法を理解できる。
資料アーカイブ 20170508版
合成抵抗
複数の抵抗を組み合わせたときに、それが全体として何[Ω]の抵抗として振る舞うか、を考えたものを合成抵抗と言います。
別の言い方をすると、抵抗を組み合わせたものと「等価」な抵抗を求めます。等価とは、流した電流と両端の電圧の関係が同じになる、ということです。
この合成抵抗の計算には、大きく二つの役目があります。
一つ目は、自分の欲しい抵抗値を作り出すための手段です。
さまざまな回路の設計などによって、ある特定の数値の抵抗が必要になります。
一方で、市販されている抵抗はE24系列という数値:
10,11,12,13, 15,16,18,20, 22,24,27,30, 33,36,39,43, 47,51,56,62, ,68,75,82,91
や、E96系列という数値に10のn乗をかけたものでしか、標準的に用意されていません。また、値の範囲も入手性が良いのは概ね10[Ω]~1[MΩ]くらいの範囲です。
つまり、10,11,12...82,91,100,110,120...910,1k,1.1k,1.2k... 910k,1M という抵抗のみです。
加えて、これらを全て用意しておくことも現実的では無いため、手元には代表的な抵抗値しか常備していないかもしれません(電子回路の本業でもないと、なかなかフルセットはそろえない)。
そのようなときに、必要になった抵抗値を作り出すために、合成抵抗で用意します。
※ある程度数があるなら、特注するという手もあるにはあるが
同じように意図的に複数の抵抗を使う場合に、電力の分散を目的にする場合があります。
メカトロにおいては、抵抗での消費電力が問題になるケースがあります(たとえば、モータの制動時に(期待せずに)発電してしまった電力を熱にして捨てる、など)。単一の抵抗では、その許容電力が持たない場合に、複数にわけることで全体で持たせる、という場合です。
機器などで、明らかに同じものが複数並列接続されている場合には、この目的のことがよくあります。
同時に、電流を分散させることにもなり、全体の消費電力を下げる効果もあります。
二つ目は回路の解析などにおいて、複数の部品がつながっているときに、それをまとめて計算するために使います。
この場合は、しばらくあとになりますが、抵抗だけではなく、コンデンサやコイルもまとめて同様に計算する手段があります。
今回は、もう一つ、合成抵抗の計算方法などを通して、回路の計算の仕方を見ていくことも目的にします。
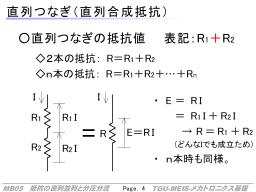
抵抗の直列つなぎ
回路内のどこかに、抵抗が2本直列につながっていたとします。
この抵抗には電流Iが流れています。分岐はないため、二つの抵抗には同じ電流が流れます。
これと同じ働きをする単一の抵抗Rはどのような抵抗か、ということが直列つなぎ、直列合成抵抗の問題です。
結論からいえば、
- R=R1+R2 (2本)
- R=R1+R2+...+Rn (n本)
となります。
右図のように、電流Iが流れているときの、両端の電圧を考えます。
合成したものは、E=RI、抵抗が2本直列になったものは、それぞれにかかる電圧が重なったものとなるため、R1I+R2Iとなります。
これが、どんなIでも等しくなる、と考えると、R=R1+R2という式が出てきます。
つまり、抵抗の直列つなぎのなかの「+」は電圧を加算したときの+です。
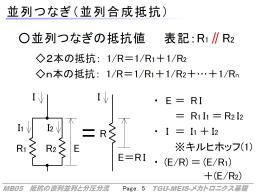
抵抗の並列つなぎ
同じように並列つなぎを考えます。
並列つなぎにしたところには分岐点があり、2本の抵抗に流れる電流は別の物になります。
また、その分岐点ではキルヒホッフの第1の法則が成立するため、I=I1+I2となります。
一方で、並列に繋いだ個々の抵抗と、合成したあとの抵抗と、両端の電圧は等しくなり、E=RI=R1I1=R2I2です。
後者の式をIについて解き、前者に代入すると、並列つなぎの式
- (1/R)=(1/R1)+(1/R2) (2本)
- (1/R)=(1/R1)+(1/R2)+...+(1/Rn) (n本)
が得られます。
つまり並列つなぎの式の「+」はキルヒホッフ第1の法則に由来しています。
この並列つなぎには、簡略化した計算方法があります。
まず、同じ抵抗値の抵抗をn本繋いだときは(R/n)になります。これは上述のような電力や電流の分散をするときに役立ちます(一般には同じ部品を複数並べる)。
抵抗が2本の時には、R=(R1×R2)/(R1+R2) という計算式があります。
これは上の式を通分して逆数にしただけです。現実的には2本並列が多いため、この式を覚えておくと計算が少し早くなります。
ただ、この式は分子分母がどちらがどちらか忘れやすいという弱点があります。その場合は単位を計算すればすぐに確認できます。
この式での単位は、[Ω][Ω]/[Ω]=[Ω]になっています。もし間違うと、1/[Ω]になってしまうため、区別できます。
このように、数値の計算だけではなく、単位での計算も合わせて行うと間違いを減らしやすくなります。
なお、これらのつなぎ方では、いちいち直列、並列というと面倒なので、直列は「R1+R2」のように計算式そのままの表記を、並列は「R1∥R2」のように「平行」の記号をつかって表します。よく見かけますので覚えておくとよいでしょう。
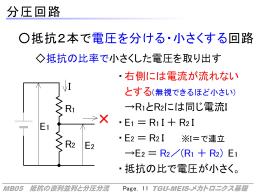
分圧回路
分圧回路は、「電【圧】を【分】けて小さくする」回路です。
右図のような回路を考えます。この抵抗2本の回路の左側は、なにか電圧を出す回路があると考え、その電圧をE1とします。
右側には、この回路でできた電圧E2を受け取る回路があると考えますが、そのときに右側の回路には電流が流れていかない(現実的にはゼロは無理なので、無視できるくらい小さい)とします。
このとき、抵抗には電流Iが流れているとします。右側には電流が流れないので、R1とR2の間に分岐点はありますが、R1とR2には同じ電流Iが流れることになります(逆に、もし右に流れると、ここで食い違いが出る)。
このとき、直列つなぎと同じように考えて、E1=R1I+R2Iとなり、また、E2はR2の両端なので、E2=R2Iとなります。
これを解くと、E2=(R2/(R1+R2))E1 という関係が得られます。
つまり、右の回路に提供される電圧は、抵抗の比率でE1を小さくしたもの、になります(抵抗値の設定によって、0~1倍)。
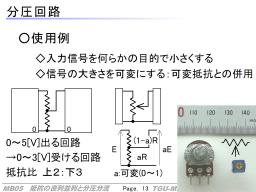
この回路は実用的な回路ではよく見られます。
たとえば、0~5[V]が出力されるセンサを、0~3[V]を受け入れられる回路に繋ぐ場合があります。
(より現実的には3.3[V]。機器の制御などに用いられるコンピュータ、マイコンにはセンサなどの信号を入力する機能があり、一般には電源の電圧がその上限になる。今時は3.3[V]動作のマイコンが多い。一方、少し前までは5[V]が一般的で、そのころにマイコンに直結できるように開発されたセンサは、0-5[V]の出力をするものが多い)
また、多くの可変抵抗器は端子が三つあり、内部は2本の抵抗が右図のようにつながったものと考えられます。
可変抵抗にも抵抗値があり、その抵抗値Rに対して、一方はaR,もう一方が(1-a)Rで、両端ではつねにRになります。
このaがそのまま分圧の比率(E2=aE1)になり、回して調整することで電圧の比率を変えられ、出力の調整などに用いられます。
※多くの可変抵抗では軸などを回す角度に比例してaが0-1で変わるもの(Bカーブ特性と呼ばれる)が多いが、ものによっては単調増加はするが比例しない場合もある(Aカーブなど)
ただし、この回路には強めの制約があります。
- 後続の回路には電流が流れてはならない=後続の回路の入力の設計の制約 (or無視できるほど小さい電流)
- 前段の回路にとっては、抵抗R1+R2がつながっているように見え、それを繋いだことで電圧が変わらないようにしなければならない=前段の回路の出力の設計制約
この制約を無視すると、意図した通りの電圧が出てこないことになります。
とはいえ、いずれも、現実的に設計可能な条件です。このような制約があるということを覚えておけば、対策は取れます。
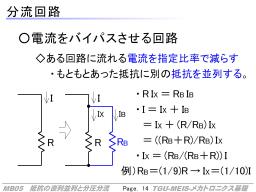
分流回路
分圧回路とセットで紹介されるものに分流回路があります。
分圧回路が抵抗の直列に対応するなら、分流回路は並列つなぎが対応します。
右図のように、すでに抵抗Rがあるところに、別の抵抗RBを並列に追加したとします。
そのとき、元の抵抗に流れる電流は、Ix=(RB/(RB+R))I と小さくなります。
これは、電流が抵抗RBにバイパスされたためです。
たとえば、もとの1/9の抵抗を並列に繋ぐと、元の抵抗に流れる電流は1/10になります(9/10はバイパス側)。
この回路は分圧回路に比べると活用される機会は圧倒的に少ないのですが、たとえば、電流計に抵抗を並列することで、より大きな電流まで測れるようにするために使えます(テスターなど原理)。
B06:コンデンサとコイル
概要と到達目標
今回は残りの主要な受動要素である、コンデンサとコイルについて解説します。
到達目標:
- コンデンサの特性を、定性的に/式で説明できる。
- コイルの特性を、定性的に/式で説明できる。
- コイルの重要さと危険性を説明できる
資料アーカイブ 20170522版
B07:アナログ信号とアナログ回路
概要と到達目標
今回は回路におけるアナログがどういうものか、その特性の見方や、扱う上での注意事項を示します。
到達目標:
- アナログ信号とデジタル信号の違いを説明できる。
- 周波数特性について説明できる。
- アナログ信号の取り扱いについて注意を払うことができる。
資料アーカイブ 20170529版(修正版)
B08:デジタル信号とデジタル回路
概要と到達目標
今回はコンピュータを初めとする今時の多くの電子機器や、工場などの設備を動かすシーケンス制御システムの基礎となるデジタルについて扱います。
到達目標:
- デジタルの利点を説明できる。
- 2値論理と論理演算について説明できる
- スイッチによるデジタル回路を説明できる。
資料アーカイブ 20170605版
熊谷正朗
[→連絡]
東北学院大学
工学部
機械知能工学科
RDE
[| ]




![E[V]&=&R[\Omega]\,I[A]\nonumber\\I[A]&=&(1/R[\Omega])E[V]](eqn/basis.bhtml.eqn401.gif)