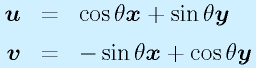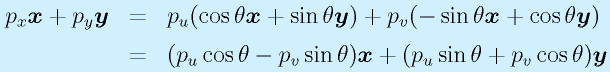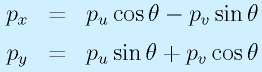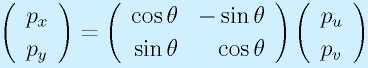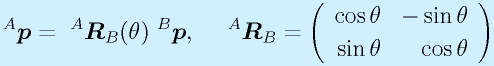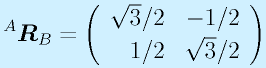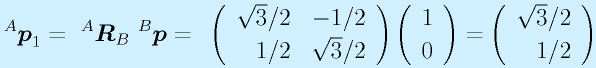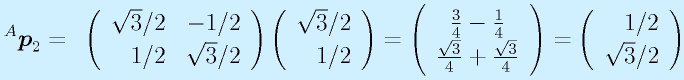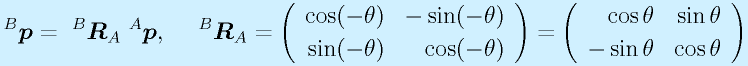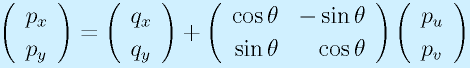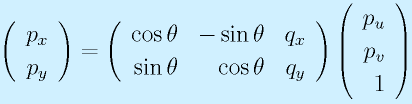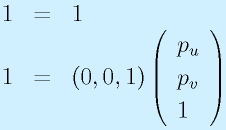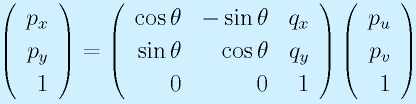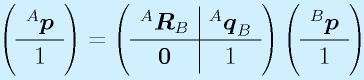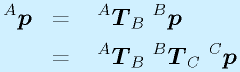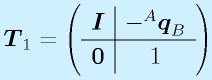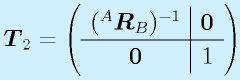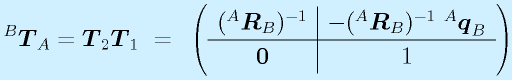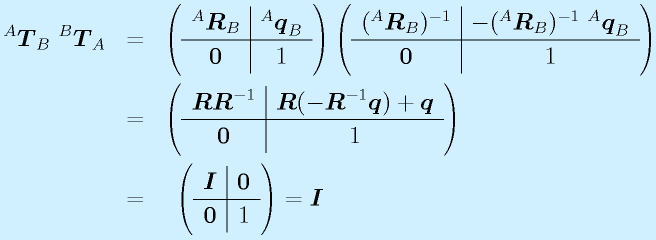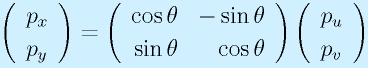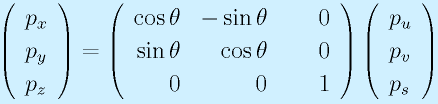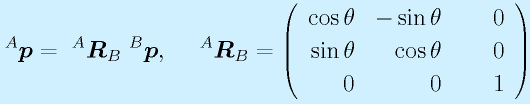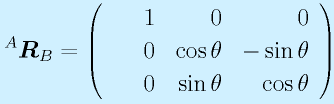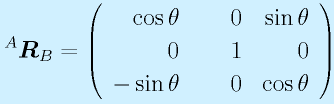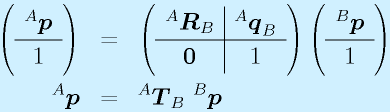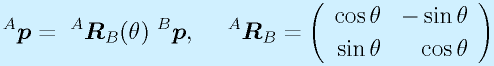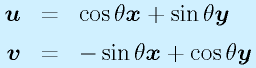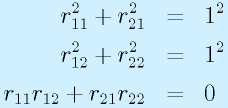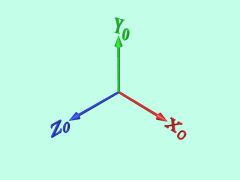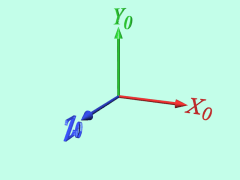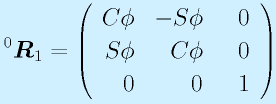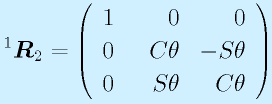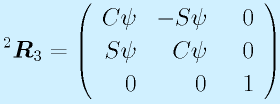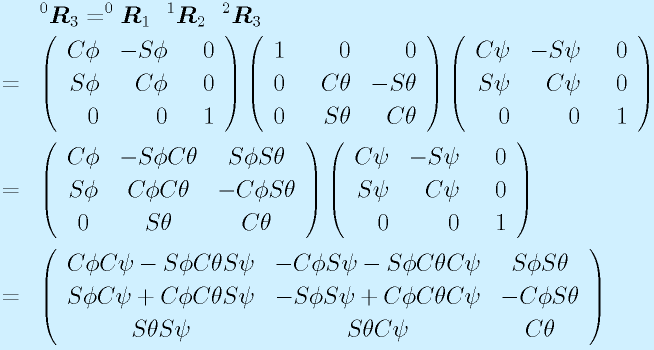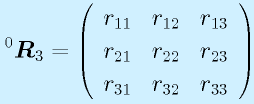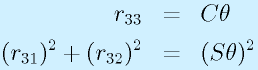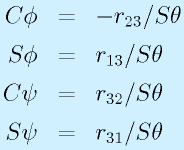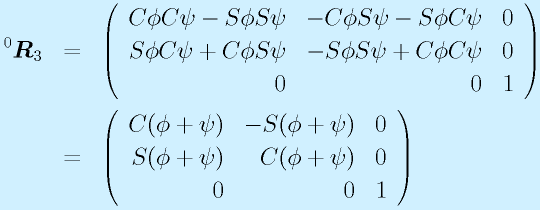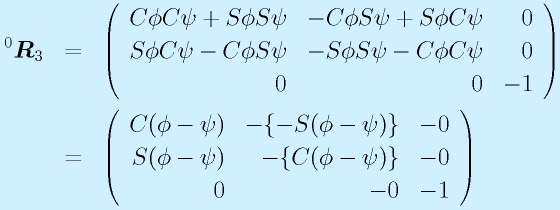ベクトルで座標を表し、行列で変換することを扱います。
ロボットの世界は3次元が基本ですが、平面上で3次元を扱うことが、そもそも分かりにくいことなので、ここでは主に2次元平面を扱います。
2次元と3次元、異なる点はいろいろありますが、3次元はだいたいは「2次元+1」か「2次元×3」なので、まずは2次元でしっかりイメージをつかみましょう。
表 記
これから座標を扱うに当たって、表記の仕方を原則として以下のようにきめておきます。
複数の座標系
 座標変換についてふれる前に、座標系を複数持つということを考えておきます。
座標変換についてふれる前に、座標系を複数持つということを考えておきます。
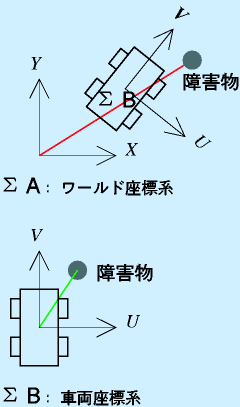
たとえば、右図のように平面上をそこそこ自動的に走る車両を考えます。
車両の走行経路に障害物がある場合、それを検知してよける必要があります。
この時、いろいろなケースが考えられます。
- 車両は屋内の限定的な範囲しか走らないので、天井にカメラをつけて障害物を検出することにした。
→ 障害物は部屋の座標系で場所(座標 x,y)がわかる(より厳密にはカメラの画像上の座標)
- 車両はいろいろ走るので車両側にセンサを搭載して、障害物を検出することにした。
→ 障害物は、車両から見た位置=車両に固定した座標系上でその位置(座標 u,v)がわかる。
- 車両はあらかじめ地図上で設定した軌道にそって走る
→ 車両の位置は、地図上の座標で把握し、ずれに応じて車両制御をする必要がある。
- 車両は自分でターゲットを見つけて、それに向かって走れば良い
→ 対象の位置が車両から見てわかれば良い
などなど。
これらの例では少なくとも、「車両が移動しても、止まっているものの座標は変わらない」場合と、「車両が移動すると、止まっているものでも相対的に座標が変わる」場合があります。
最終的には、どちらかに統一して、センシングした情報を処理して、駆動しなければ混乱しますが、地図情報はやっぱり動かない座標で書いてあるものですし、車両上のセンサが検出した障害物の位置は、車両からみた相対位置です。
このように、ロボットを扱おうとすると、複数の対象に固定された複数の座標系がしばしば出てきます。
上の例は、せいぜい地上の座標系と車両上の座標系のみを考慮すれば済みますが、同じ移動する座標であっても、2脚歩行ロボットなどは、「胴体を基準にした座標系」「右のふとももを基準にした座標系」「右のすねを基準」「右足を基準」「左...」と非常に多くの座標系がでてきます。
ただし、それらの座標系はそれぞれ、何らかの関係をもって互いに運動しています。
その座標系同士の相対的な関係をもとに、その座標系の上に乗っているものを、別の座標系からみるとどこに見えるか、を以下で考えてみます。
※多くの座標系を扱うときに、一つ基準となる、動かないとする座標系を考えることがあり、ワールド座標系と呼ばれます。
もっとも、動かないと思っていても、たとえばそれを実験室の床に固定すると、地球は自転するわ、公転するわ、銀河系は回ってるわ、それなりに動いています。
そこまでは屁理屈をこねず(笑)、床に固定したら動かないと考えることにしましょう。
座標変換の分解
 ここでは座標の変換として、合同な(大きさ形が変わらない)変換のみを、まずは考えます。
座標の変換と言った場合には、拡大縮小や正方形を菱形にするような変形もあり得ますが、合同な変換を考えてからにしましょう。
ここでは座標の変換として、合同な(大きさ形が変わらない)変換のみを、まずは考えます。
座標の変換と言った場合には、拡大縮小や正方形を菱形にするような変形もあり得ますが、合同な変換を考えてからにしましょう。
合同な場合に限るのは、一つには話が簡単になるからですが、ロボット工学という分野を考えた場合、物体の運動や関節の角度変化などでは、ものそのものの大きさは変わらず、それに固定された座標系も形を変えないためです。
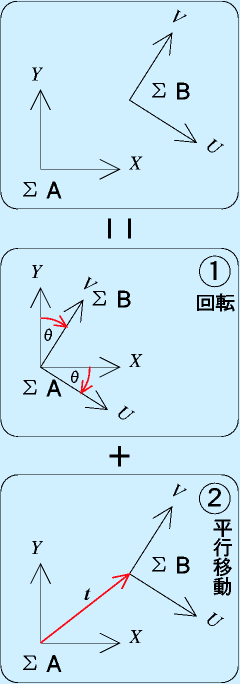
合同な座標変換は「平行移動」と「回転」の組合わせで出来ます。
右図は、先ほどの二つの座標系の関係を分解したものです。座標系Aをまず適当な角度θだけ回転させ、それをベクトル t で平行に移動します。
これで、座標系そのものの移動ができます。
あとは、座標系の移動にともなってその座標に乗っていたものがどう移動するか、あるいは、ある座標系上のものが別の座標系からどう見えるか、について確認しましょう。
ちなみに、先に平行移動してから回転させることももちろん可能ですが、この図と同じ角度、移動量のままで順番だけかえると違う結果になることはわかると思います。平行と回転とか、回転でも3次元になって回転軸の異なる回転を組み合わせるときは、適用の順番が非常に重要になります。
ここでは、回転させて移動、のほうが分かりやすいとおもって、この順番にしました。
平行移動
 平行移動は非常に簡単です。座標を単に加えるだけです。
平行移動は非常に簡単です。座標を単に加えるだけです。
簡単なので、座標変換の意味をちょっと考えてみます。
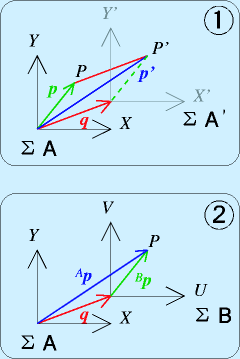
おそらく、いままで、平行移動といった場合に、たびたび出てきて、ぱっと思い当たるのは右の図の(1)だとおもいます。
座標系A上の点、P(位置ベクトル p )を q だけ平行移動すると、P'( p' )に移動する、という扱いです。
この場合は、座標系A(X-Y)が移動してできた座標系A'(X'-Y')の存在は薄いかもしれません。
それに対して、ロボット工学では座標系の存在をはっきりと意識します。右図(2)では、二つの座標系AとBがあります。
この節では便宜的に平行移動といっていますが、実際にAが移動してBになる必要もありません。
ある点Pを座標系Aから見たとき( Ap )と、座標系Bから見たとき( Bp )では、その座標は異なり、その関係を扱います。
また、座標系Bの上で見ていた座標を、座標系Aで表現するとどうなるか、という演算をたびたび必要とします。
上の例にもあるように、移動する車両から見つけた障害物が部屋のなかではどこにあるか、または、ロボットが持っている部屋の地図の上の目標点はロボットからみてどの位置にあるか、などです。
こういった概念は、これからしつこく座標をいじっているうちに身に付くと思いますが、最初はしっかり意識しておきましょう。
さて、座標系Aからみた、座標系Bの原点位置が q で表される場合、図からも明らかな以下の式が成り立ちます。
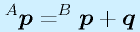
もう少し、意識して書くと、
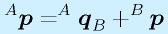
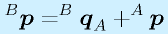
となります(座標系AでみたBの原点、座標系BでみたAの原点)。なお自明ですが、
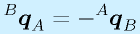
が成り立ちます。
また、なんとなく、左肩と右下の添字がきれいに関連して見えますが、見た目の問題で、常にその本質を考えて式を見るようにしてください。
決して、文字がつながるから、という理由だけで式を書いてはなりません。
(※蛇足: 個人的には、'q' ではなく translationの't' と書きたいのですが、混乱を避けるため、教科書に準拠して 'q' と書きます)
また、この変換で移動するのは座標(位置ベクトル)です。ある点と点の相対的位置関係を表すベクトル(相対ベクトル)は、当然ながらかわりません。
その意味で、平行移動は線形な変換ではありません。
(線形な変換の場合は、「Aを変換したものとBを変換したものの和は、A+Bを変換したもの」になりますが、
( a + q )+( b + q ) != ( a + b )+ q ) となり、線形では
ありません。)
回転移動
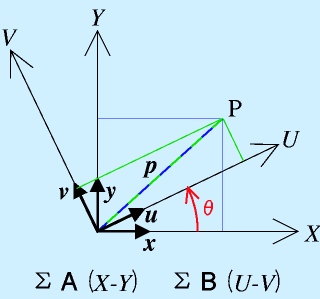 つぎに、座標系の回転を考えます。
つぎに、座標系の回転を考えます。
原点が共通な座標系A(X-Y軸)と座標系B(U-V)軸からそれぞれ点Pを見ます。
ここで x,y はX,Y軸の単位ベクトル、 u,v はU,V軸の単位ベクトルとします。
両者の成す角がθの場合、
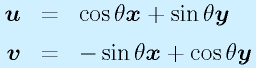
となります。
一方、点Pを指すベクトル p は、
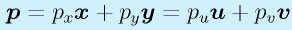
と、それぞれの座標軸の単位ベクトル成分に分解でき、
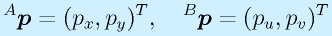
に他なりません。
以上の式を結合して、
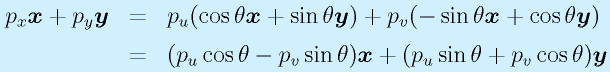
となり、 x,y が任意であるため、
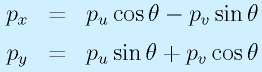
が成り立ちます。まとめると、
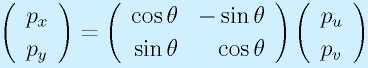
となり、
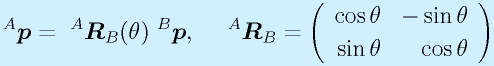
という形に書けます。
回転の場合、直感的に分かりにくいこともあるため、実際に数字を入れてみることが肝心です。
例:θ=30度
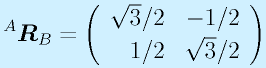
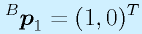
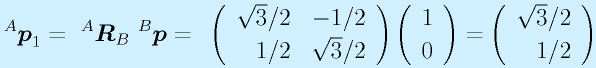
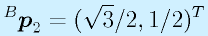
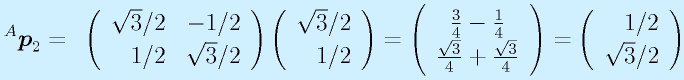
これらの座標軸やその上の点を実際に手で書いてみて、(0,1)など数値的に検証のしやすい他の点も試してみるようにしてください。
この関係は座標軸AとBでどちらが主ということはありません。そのため、両者の関係を入れ替えると、
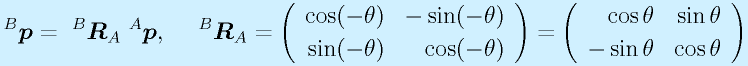
になります(入れ替えたとき、角度も逆向きにすることに注意)。さらに、
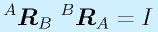
すなわち
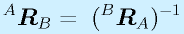
が成り立つことも重要です。つまり、回転に関しては、逆行列が逆変換を表すことになります。
平行移動と回転
以上のことをまとめると、二つの座標系の間の座標変換は次の式で得られることがわかります。
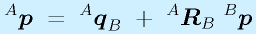
まず、 R で回転させ、ついで、 q だけ平行移動させます。
(やっと教科書にたどり着いた!)
同次変換
ロボットで座標の関係を扱うとき、多くの座標系がでてきて、変換ごとにこのように書くと面倒です。
そこで、この式を行列とベクトルの乗算だけに書き換えます。
まず、一度この式を成分ごとにばらしてみます。
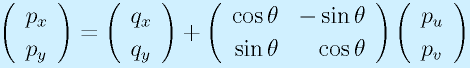
これは、
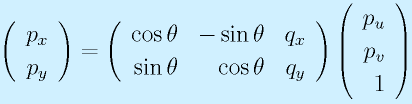
と書き換えることができます(行列表現を分解してみると同一です)。
つぎに、これに式を一本加えます。
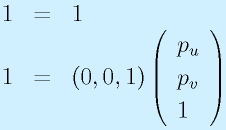
これらをまぜると、
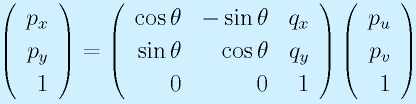
と表記できます。まとめると、
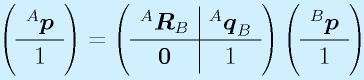
となります。これによって、回転+平行という一般的な座標変換が
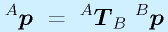
という分かりやすい形で書けるようになりました。つまり、
- 本来の座標ベクトルの次数を一つ増やし、「1」を追加する。
- 回転変換の行列の行と列を一つ増やし、増えた列に平行移動のベクトルと「1」を追加し、のこりは0をうめる。
という処理をします。
同次変換のご利益=変換の連続
座標系を3つ、A,B,C を考えます。
AとB, BとCの関係がわかっている場合、すなわち
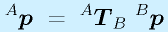
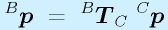
の場合に、AとCの関係は単純に、
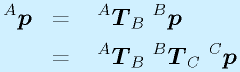
で表せます(代入しただけ)。つまり、AとCの関係も単純に
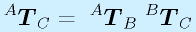
と、同次変換行列を重ねておしまいです。
同次変換の逆変換
つぎに、逆変換について考えてみます。
AとBの関係をつくったとき、 R で回転させてから q で平行移動しました。
基本原則として、これらの変換には順番があります。
つまり、 q だけ移動してから R 回転した場合は、別の変換になってしまいます。
さて、「 R で回転、 q で移動」という手順を逆変換するには、「 q だけ戻す、 R で逆回転」という手順になります。操作の符合が逆になることにも注意してください。
この操作をまずは別々の変換、T1とT2で書いてみます。
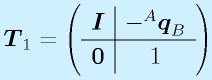
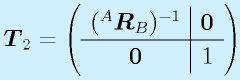
結合して、
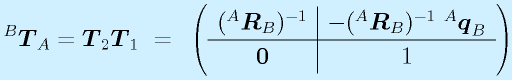
ここで重要な点は、「あとでする変換を前に書く」ことです。変換されるベクトルに近い=右から、変換行列を並べるためです。
さて、逆変換の同次変換行列が求まったところで、その性質を確認しましょう。
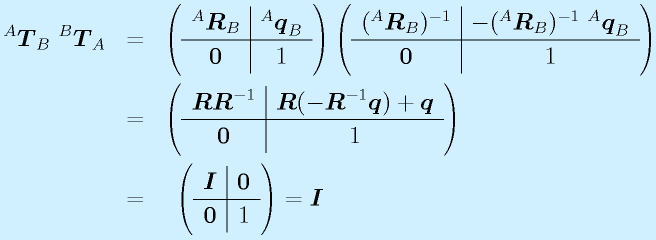
つまり、
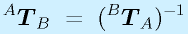
と、同次変換についても、逆変換は逆行列で行えることが確認できました。
- 変換を連続して行う場合、同次変換行列は、最初に変換するものを右に、順に左に並べていく。
- 逆変換は逆行列をつかえばよい。
このように、同次変換を用いると、ややこしい座標変換が一見すると単純な行列一個になります。
もちろん、中身はややこしいのですが、それは実際にロボットを設計するときに考えることにして、ロボット工学の講義としては、この次の節でややこしいのを終わらせて、あとは行列でさくっと書くことにしましょう。
※つぎもまだ数式がややこしいことを予告。
いままで話を簡単にするために、2次元で説明しておきましたが、ここで3次元に拡張しましょう。
ここからは、イメージ力が重要です。
要素の数
2次元では、座標(ベクトル)要素数は2個でした。当然ながら、3次元では3個になります。
また、回転を表す行列は、2×2から3×3になります。
後述するように、同次変換の概念はそのまま持っていくことができ、同次ベクトルの要素数は4になります。
同次変換行列も4×4になります。
平行移動
平行移動は2次元において、座標系の原点間を示す単なるベクトルを加算することで行っていましたが、3次元になっても考え方は変わりません。
座標が3要素になるので、加えるベクトルも3要素です。
※本ページ冒頭で書いた「3次元は2次元+1」に相当。
回転
この回転が3次元での扱いをやっかいにする代物です。
ここであつかった2次元での回転は、原点を中心とした回転でした。
これをそのまま3次元に拡大すると、「原点を通る軸を中心に回転」となり、特に扱いの容易な座標軸を中心とした回転を考えます。
たとえば、2次元のときの回転の式、
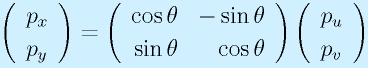
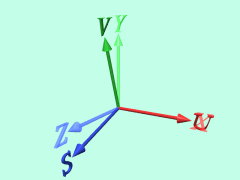
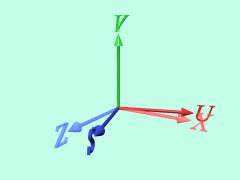
に対して、新たに座標系AにZ軸、座標系BにS軸を加えます。
ここで、右手系の定義にしたがって、 x × y = z となるようにZ軸を取ると、図に垂直に手前方向が正の方向となります。
図の面内での回転をそのまま3次元的に見て、Z軸まわりの回転と考えます。この場合、S軸はZ軸そのままになります。
すると、この回転の式は拡張されて、
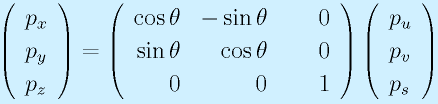
となります。このとき、2次元と同じように、
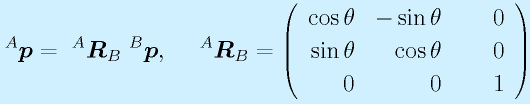
と書くことができます。
同じように、X(U)軸回りの回転として、
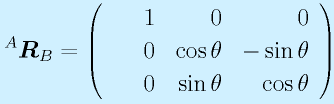
同じように、Y(V)軸回りの回転として、
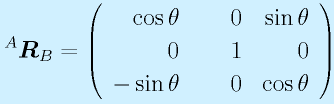
が定義できます。
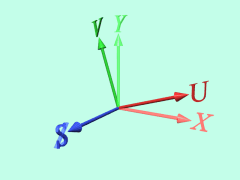
ここで回転方向について確認しておきます。
ある軸周りといったときには、正の向きを決めておかないと2方向があるからです。
最初の例で見てみると、「Z軸まわり」といったときに、回転角度θの方向は、「座標軸の正の方向に親指を向けて、右手で軸を握ったときに、指が巻かれる方向」が正になっています。
残り二つもそのようになっているはずですので確かめておきましょう。
こういう軸の性質として対象な操作を考えるときに覚えておくと便利な考え方として、「x→y, y→z, z→xと置き換える」という方法があります。
たとえば、座標軸の基本ベクトルの性質 x × y = z に対して、
y × z = x (置き換え1回)、
z × x = y (置き換え2回)が成り立っています。
だいたいはこのパターンが成り立つと思いますので、覚えておくと一種類覚えておけば残りも導けますので便利です。
回転軸の設定方法はいくらでも考えられそうですが、この3つを組み合わせると、任意の回転が得られることはこのあとで確認します。
※「3次元=2次元×3」に相当。
同次変換
平行移動も回転移動も3次元でも2次元と同じ形、
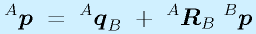
と、 R の回転と、 q の平行移動で表すことができます。ただし、要素の数が増えている点のみが違います。
そのため、3次元についても上で説明した同次変換の考え方、
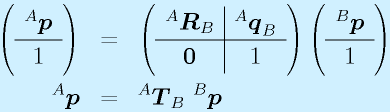
がそのまま使えます。また、これから導き出した、
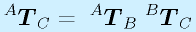
や
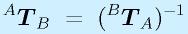
がそのまま成立します。
回転変換の検討@2次元
ここで、回転を表す行列 R の中身をよく見てみます。
2次元の場合でみて、
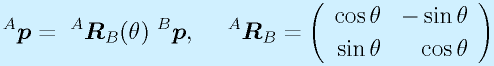
ですが、そもそもの導出の前提、
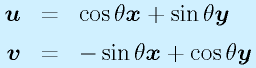
と見比べると、 R の第1列目が u の x 成分と y 成分そのものを表していることがわかります。
同じように、第2列目が v の x 成分と y 成分です。
つまり、座標系B上の点を座標系Aに変換するための行列A R Bは、座標系Aで見た座標系Bの各軸の基本ベクトルを並べたものになっています。
当たり前といえば、当たり前ですが。
ということは、 R の成分を好きにつくることでも、任意の回転を表すことができます。
ただし、選び方には制約があります。
2次元で考えると、要素数は4個ありますが2次元での回転は1変数しかありません。
これは、「合同な変換のみを扱うこと」にしたことに起因します。つまり、「座標軸が伸び縮みしない」=「単位ベクトルの長さは1」、「直角は直角のまま」=「単位ベクトル同士は垂直」=「単位ベクトル同士の内積が0」という条件があるためです。
2次元の R で考えると、
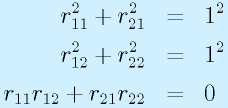
となります(長さ=1は自乗した形で比較)。
上記行列に対して、これが成立することを確認しておきましょう。
なお、列ごとに分割することに注意してください。
結果的に、数値は4個あるけど、制約が3個あるので、自由になるのは1要因のみ、ということになります(1要素とはちょっと違います)。
補足:
行ごとに分割しても同じ結果が得られます。これは、このような性質の行列(直交行列)の場合、
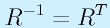
が成り立つことに起因します。ある回転の行列に対して、その逆行列もまた回転の行列(逆変換)です。逆行列を求める代わりに転置しても同じなので、行方向に分割しても同等の性質が出てくることになります。ただし、ここではあくまで列ベクトルを組み合わせたものとして認識しましょう。
3次元での回転の自由度
まずは、上の考え方をそのまま持ってきて、「数」で考えてみましょう。
3次元の回転の行列は3×3で9要素です。
これは、2次元と同じく、一方から見た他方の座標軸の単位ベクトルを並べたものになります。
そこで、それらの制約を考えると、1:「単位ベクトルの長さは1」→3制約、2:「互いに直交」→3制約、合計6制約となります。
残りは3なので、軸回りの回転を3回すれば、任意の回転を表せるように思われます。
以下では、本当に3個で表せるかを考えてみます。
さて、3つの回転で表せるとしても、非常に様々な手順があり得ます。
角度の場合、回転させる順番を変えてしまうと異なる結果になります。
そこで、2つの姿勢の表し方を例示します。
ロール・ピッチ・ヨー角
素直な?表現法にロール・ピッチ・ヨー角の表現があります。
これは3つの軸回りに順に回転させます。
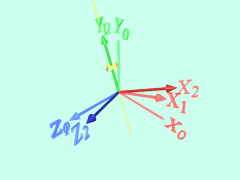
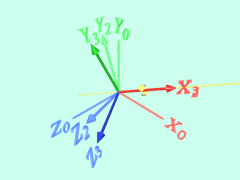
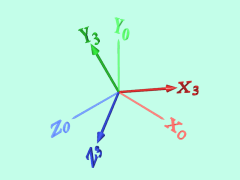
以下の例では、Z・Y・X軸回りに順に回転させています。
まず、もとの座標系X0-Y0-Z0をZ0(=Z1)軸回りに回転させて、座標系X1-Y1-Z1をつくります。
次に、X1-Y1-Z1をY1(=Y2)軸回りに回転させて、座標系X2-Y2-Z2をつくります。
最後に、X2-Y2-Z2をX2(=X3)軸回りに回転させて、座標系X3-Y3-Z3をつくります。
この表示法は飛行機の姿勢を表す際によくつかわれ、座標系の取り方にもよりますが、鉛直軸回りをヨー(yaw)軸、左右の傾きをロール(roll)軸、前後の傾きをピッチ(pitch)軸といいます。
車などの揺れでもローリングだのピッチングだのいうことがありますが、これです。
なお、本によって回転順序が異なったり、回転軸をZ0,Y0,X0にとっていたり、いくつか種類があることに注意が必要です。
とりあえず、3軸順番に回せば姿勢を表すことができる、と覚えて、実際に使うときは手元の本や似た論文を参考にして座標系を設定して、自分の仕事のなかで一つに固定すればいいと思います。
自分のなかでもごちゃごちゃにするとたいへんですので注意しましょう。
※) これまで、座標系は ΣA(XYZ)とΣB(UVS)で表記していましたが、座標系が多くなって文字が明らかに足りなくなるので、Xn-Yn-Znと表記を変えます。
ただしこの表記法では、この座標系での位置ベクトルの要素を考えようとすると添字がごちゃごちゃになるので要注意です(中身を考えなければ問題なし)。
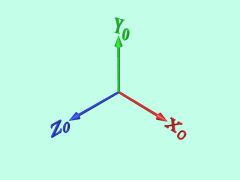
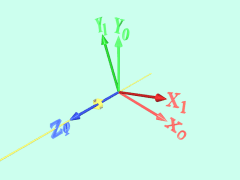
Roll-Pitch-Yaw アニメーション, 320x240 (2018/04/17, 211,925 bytes)
Roll-Pitch-Yaw アニメーション, 640x480 (2018/04/17, 544,725 bytes)
オイラー角
力学などでも出てきて頭を悩ますものにオイラー角があります。
(オイラーはあちこちの分野で有名な式だの法則だのを提示したため、どれがどれだか難儀で、個人的には苦手な名前です(笑))。
ロール・ピッチ・ヨーは納得しやすいとおもいますが、これは回転軸をZ-X-Zとして、Y軸をつかいません。
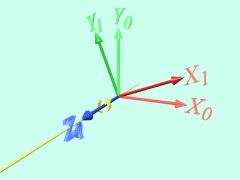
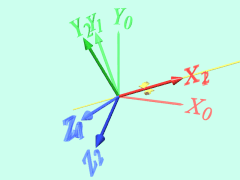
まず、もとの座標系X0-Y0-Z0をZ0(=Z1)軸回りに回転させて、座標系X1-Y1-Z1をつくります。
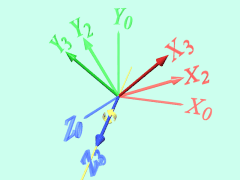
次に、X1-Y1-Z1をX1(=X2)軸回りに回転させて、座標系X2-Y2-Z2をつくります。
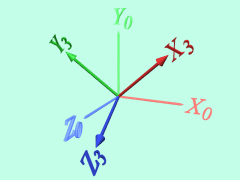
最後に、X2-Y2-Z2をZ2(=Z3)軸回りに回転させて、座標系X3-Y3-Z3をつくります。
これまた本によって書いてあることが微妙に異なります。
指定教科書では「Z-X-Z」で書いてあって「Z-Y-Z」のこともあるとありますが、別の教科書では「Z-Y-Z」が書いてあります。
また、ここで例示したようなものを「Z-X-Zオイラー角」と限定的に表記して、オイラー角そのものを任意の3軸の回転として表記(ロール・ピッチ・ヨーもその一種に含めてしまう、Z-Y-X)するものもあります。また、本によっては、回転軸が変換とともに動くものをオイラー角と称すると書いてあったり、どれが正解かわかりません(一番厚い本を信じてみるとか(^^;; )。
ここでは、3軸すべてを使わなくとも、2軸を交互に使うことでも角度を表記できると認識しておくと良いでしょう。
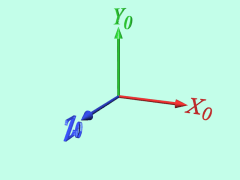
オイラー角 アニメーション 320x240 (2018/04/17, 266,325 bytes)
オイラー角 アニメーション 640x480 (2018/04/17, 656,725 bytes)
オイラー角の解析
上記オイラー角での回転を数式で考えてみましょう。
まず、Z軸回りの回転(0→1)の角度をφ(phi, ファイ)として、
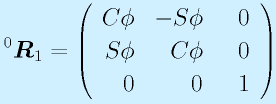
となります。ただし、

と置き換えています(この先面倒なので)。
つぎにX軸回り(1→2)の角度をθとして、
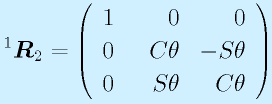
を得ます(同じ置き換えパターン)。最後のZ軸回り(2→3)の角度をψ(psi, プサイ)として、
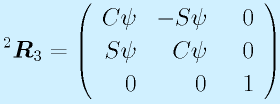
となります。
角度(φ, θ, ψ)で表される回転を総合して得られる回転行列は、
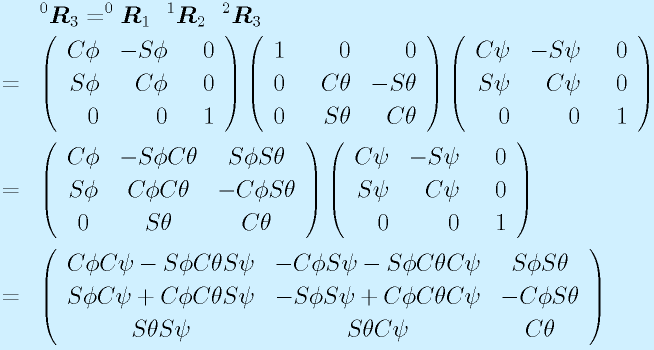
となります。
さて、
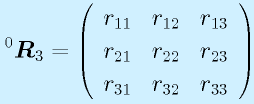
が、回転行列の性質を満たしつつ任意に与えられたときに、角度(φ,θ,ψ)が求まるかを確認してみます。
まず、
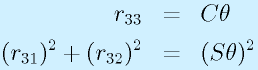
から、θを決定できます(ただし、sinθの符合の決め方で2通り。符号は直前との連続性などを考慮して決定)。
実際には、r33から直接アークコサイン(acos, cos-1)で求めることもできますが、sinも用意しておくとアークタンジェント(atan,tan-1)で計算されます。
次に、sinθ≠0の場合は、
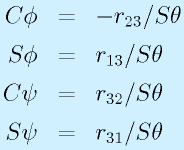
でφ、ψを求めることができます。アークタンジェントを使うならば、-r13/r23, r31/r32から直接求めることもできます。
※実際にはcos成分がゼロになっているとゼロで除算する問題が起きる、また角度が±90度に限られる、など注意が必要です。C言語などではatan2というこれらの問題をすっきり解決してくれる関数があります。
一方、sinθ=0の場合はr23,r13,r32,r31共にゼロとなるため、この計算が使えません。
(1) cosθ=1の場合(θ=0)
回転行列に代入して計算すると
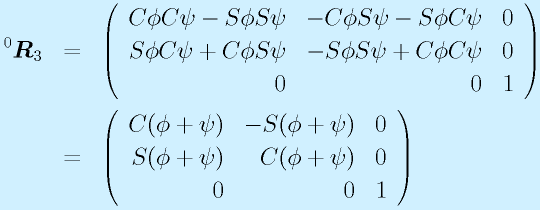
となります。これは「Z軸周りにφ+ψの回転」を意味します。
よく考えてみれば当然で、ZXZの回転でXの回転を0にしたので、Z(φ)Z(ψ)の回転になったわけです。この場合、φもしくはψを適宜決定すれば、もう一方が定まります(ψ=0とすればφがこの回転行列のcosとsinから求まる)。
(2) cosθ=−1の場合(θ=±π)
回転行列に代入して計算すると
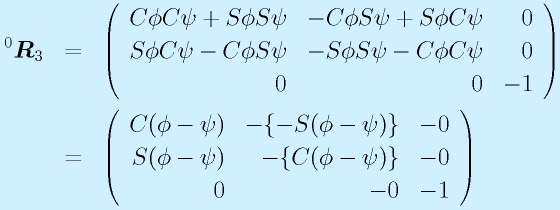
となります。基本的に「Z軸周りにφ−ψの回転」のような形で、第2,3列の正負が逆転しています(0にも敢えて−をつけた)。
これは途中でX軸回りに180度回転させたことで、同じZ軸回りの回転が逆回転になること、さらにこの過程でY,Z軸の方向も逆になることに起因します。
前例に比べて形は変にはなりますが、これでもφ−ψのcosとsinが求まるので、そこからφ−ψが求まります。一方を固定すれば、角度は全て求まります。
以上、長かったですが、ロボット工学に必要な、座標変換について終わらせました。
3次元は特に納得できるかどうかが重要ですので、あの手この手で納得してください。
おまけ
以上のように、3次元空間での二つの座標系の関係は、平行移動と回転、合計6個のパラメータで表されます。
その様子をアニメーションにまとめてみました。
6自由度 アニメーション 320x160 (2018/04/17, 439,149 bytes)
6自由度 アニメーション 640x480 (2018/04/17, 1,146,349 bytes)
1〜3は上のロール・ピッチ・ヨー型の回転変換、そのあと4〜6でX,Y,Z方向の平行移動を表しています。
(添字が3のままだったりしますけど、もともと流用して作ってみただけなのであまり気にしないこと(^^;)
これらをもとに、マニピュレータと車輪移動型ロボットについて見ていきます。
![^{\mbox{\scriptsize [基準座標系]}}\vect{p}_{\mbox{\scriptsize [普通の添字]}}^{\mbox{\scriptsize [T(転置), -1(逆行列)]}}](eqn/coordtrans.bhtml.eqn1.gif)
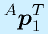
 座標変換についてふれる前に、座標系を複数持つということを考えておきます。
座標変換についてふれる前に、座標系を複数持つということを考えておきます。 ここでは座標の変換として、合同な(大きさ形が変わらない)変換のみを、まずは考えます。
座標の変換と言った場合には、拡大縮小や正方形を菱形にするような変形もあり得ますが、合同な変換を考えてからにしましょう。
ここでは座標の変換として、合同な(大きさ形が変わらない)変換のみを、まずは考えます。
座標の変換と言った場合には、拡大縮小や正方形を菱形にするような変形もあり得ますが、合同な変換を考えてからにしましょう。 平行移動は非常に簡単です。座標を単に加えるだけです。
平行移動は非常に簡単です。座標を単に加えるだけです。 つぎに、座標系の回転を考えます。
つぎに、座標系の回転を考えます。