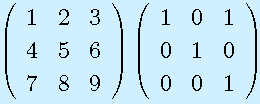
を計算せよ。
Q2:
のとき
を求めよ。
プチテストは本講義を進め、修了するにあたり、できないと困るというレベルのごく単純な計算を基本に出題しています。 ということは、このくらいはできないと合格の可能性も著しく低下するわけで、興味のみで単位抜きに受講している学生さんは別として、必ず計算できるようにしておいてください。 できるからと言って合格は保証しませんが、できないときついです。
レポートに関しては、多少まじめに計算しないと大変そうなネタを提供します。
Q1:
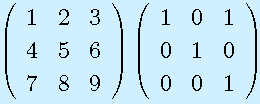
を計算せよ。
Q2:
![]()
のとき
![]()
を求めよ。
A1:
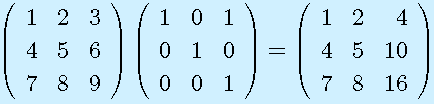
A2:
![]()
![]()
![]()
ただ計算するだけ。a×b=-b×a, ともにa,bとの内積が0となることに注意。
"-3i+6j-3k" の解答もオマケでOKとしたが、ここではijkが定義されていないので、解答としては不完全。「各軸の単位ベクトルをi,j,kとする」と付記してあれば、問題ない。