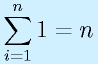まず、表計算ソフトで、できる限りのことをやってみましょう。
プログラムを作った方が、圧倒的に効率がいい場合もありますが、プログラムを作ることができる環境にくらべて、表計算ソフトを使える環境のほうが圧倒的に多く、また、準備も楽なためです。
基本的にExcelを題材につかいますが、表計算ソフトとしての考え方はExcelでもOpenOffice calcでも、演習室には入っていないものの三四郎などのソフトでも、変わりません。
ソフトの使い方(メニューの選び方)などは変わりますが、大差ありません。
なるべく、そういった部分に立ち入らないようにします。
表計算ソフト
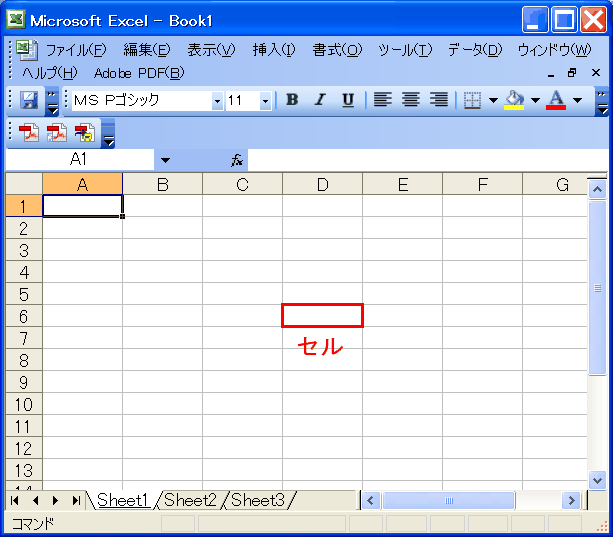 |
| 表計算ソフト |
表計算ソフトはおおむね左図のような構成です。
縦横にマス目に区切られ、それぞれの枠内に値(数値、文字列)や式を書き込みます。
まさに「表」であって、その表に式を書き込めば「自動的に計算してくれる」便利な表として使うことができます。
また、グラフを自動で書かせたり、より複雑な統計処理を行う機能もあります。
表計算では、この枠1個を「セル」とよび、すべての処理の基本単位になります。
(これは予め用意された「変数」として機能します。)
一つのセルを特定して表記するために、縦方向(行方向)と横方向(列方向)に順番に(住所として)数字やアルファベットが割り当てられています。
一般的には、縦方向は数字が1〜、横方向はアルファベットでA〜(A,B..Z,AA,AB,..AZ,BA..)がついています。
これをつかって、「D3」のセル(左から4つめ、上から3つめ)というように指定します。
また、長方形状に複数を指定する場合は、「B3:E10」のように「:」で対角のセルをつないで指定します。
式の書き方
表計算はセルに式を入力して、はじめて「ただの表」ではなくなります。
式を入力するには
=数式
という形で入れます。数値などの値はただ書き込みます。
すると、数式の値が計算されて、そのセルに表示されます。
(「=」で始まる、式ではない表示内容(文字列)を書く場合は、「'=..」と「'」を最初に入力する)
ここで、数式には、先ほどのセルを指定する「D3」などを使うことができます。
ここで、セルB1に「=A1+1」を入れると、B1の値は3+1=4となります。
この値はA1を書き換えると、自動的に計算→表示されます。
どこかでB1を使っていると、そこも引き続き計算されます。
さて、表計算ソフトが便利なのは、「数式のコピー」ができることです。
数式のコピーが値のコピーと違うところは、「式で参照しているセルも自動的に修正してくれる」ことです。
たとえば、B1の数式を、B2にコピーしてみます。すると、
| | A | B | C |
| 1 | 3 | =A1+1(4) | |
| 2 | 10 | =A2+1(11) | |
と、B1では「A1」だったところが、B2では「A2」になります。
この時の書き換えルールは相対的な位置関係によります。
「B1にとって、A1は左隣」だったので、B1の計算の仕方を「左隣に1を足す」と解釈し、B2に式をコピーするときにも「左隣に1を足す」、すなわち「A2+1」になります。
このように、式をコピーするときは、コピーする数式が使っている他のセルが、その式からみて左右にどれだけ、上下にどれだけ離れたところのものかという相対的な位置をそのままつかいます。
ただし、実際には、「常に特定のセルの値をつかいたい」こともあるわけで、そのときは「$」をつけて「これはコピーするときにいじるな」という指示をだせます。
以下、実例で確認します。
実際に操作してみてください。
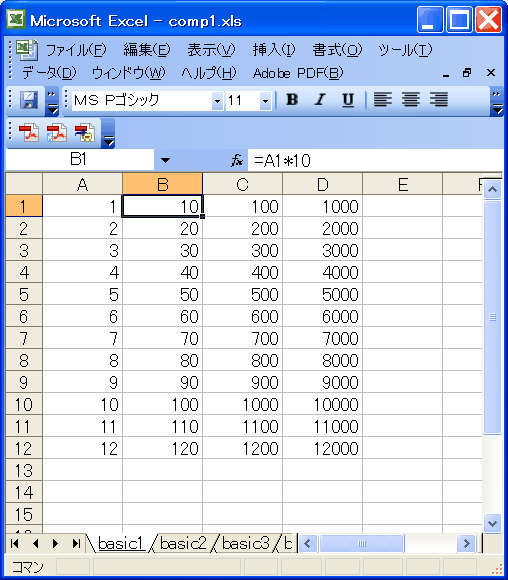 |
| セル参照に絶対指定ない場合 |
ステップ1:入力 ※括弧内は表示される値
ステップ2:A2をA3にコピー →さらにA4〜にどばっとコピー
| | A | B | C |
| 1 | 1 | | |
| 2 | =A1+1(2) | | |
| 3 | =A2+1(3) | | |
コピーは二つの方法があります。
- コピーしたいセル(範囲を選択して)でCtrl-C(Controlキーを押しながらc)→コピーしたい先にいってCtrl-V。
- ある数式を下方向、もしくは右方向にどばっと増やしたい場合には、
まず、該当する数式を左端もしくは上端に含むように範囲を選択
メニュー→編集→フィル→下方向/右方向へコピー を選択(もしくはCtrl-D/Ctrl-R)
します。なれると、後者の方が使いやすくなるとおもいます。
ここでいう「範囲」の指定とは、複数のセルを長方形の形(縦○個×横○個)まとめて選んで捜査の対象とする方法です。
その方法は
- マウスでドラッグする
- Shiftキーを押しながらカーソルを操作する
で行います。選んだところは見た目わかります。
なれると、キーボードの方が楽になります。
さきほどのメニュー選択も実は「Alt+E → I → R, D」とキーボードで操作できます。
表計算ソフトはキーボードで式を入力したりもするので、キーボード操作になれておくと操作が早くなります。マウスを使うと、持ち替えなければならないので。
なお、以上の操作は連番や一定間隔で数列を作るときに頻繁に使う手順です。
ステップ3:B1を入力、B2以下にコピー
| | A | B | C |
| 1 | 1 | =A1*10(10) | |
| 2 | =A1+1(2) | =A2*10(20) | |
| 3 | =A2+1(3) | =A3*10(30) | |
ステップ4:B1〜B?? をまとめて、C1〜、 D1〜に横にコピー
| | A | B | C |
| 1 | 1 | =A1*10(10) | =B1*10(100) |
| 2 | =A1+1(2) | =A2*10(20) | =B2*10(200) |
| 3 | =A2+1(3) | =A3*10(30) | =B3*10(300) |
同じく、方法としては、「Bを範囲指定の上Ctrl-C、C1でCtrl-V」と「B〜Dで範囲指定して右にフィル(Alt+E, I, R / Ctrl-R)」があります。
ここで、右にコピーしたときに、B列ではAを参照していたのが、C列ではBを参照するようになることに注意してください。
以上、適宜操作すると、右図のような結果になります。
絶対参照
ここまでは「式をコピーすると、参照先も相対的な位置関係で補正する」でした。
しかし、特定の数値、たとえば、なんらかの数値変換をするときの変換係数など「すべての計算で同じ値を使う」という場合には、絶対的な参照が必要です。
この場合、セルを表す「D3」などに「$」をつけます。
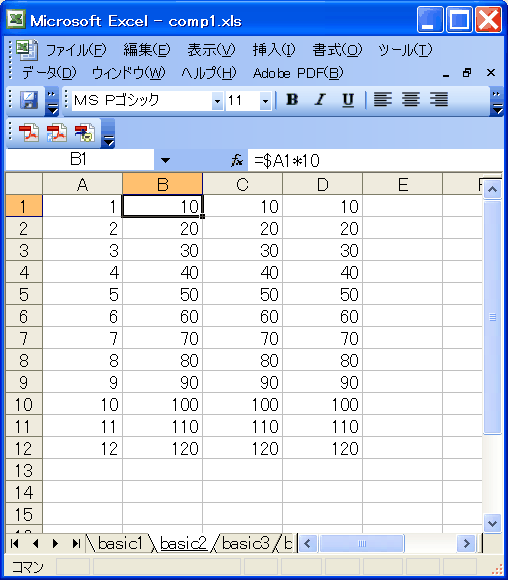 |
| 列(横)方向を絶対指定=常に特定の列を参照 |
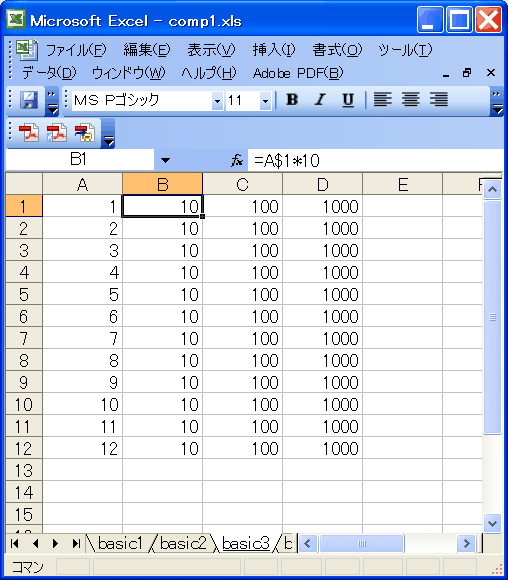
1:「$D3」型
「D」の前に$をつけています。
| | A | B | C |
| 1 | 1 | =$A1*10 | =$A1*10 |
| 2 | =A1+1 | =$A2*10 | =$A2*10 |
| 3 | =A2+1 | =$A3*10 | =$A3*10 |
この場合、コピーすると、
- 横方向(A〜)については、修正しない。「$A」はいくらコピーしても「$A」のまま。
- 縦方向(1〜)については、相対的に修正。
となります。
この形は、わりとつかいます。
 |
| 行(縦)方向を絶対指定=常に特定の行を参照 |
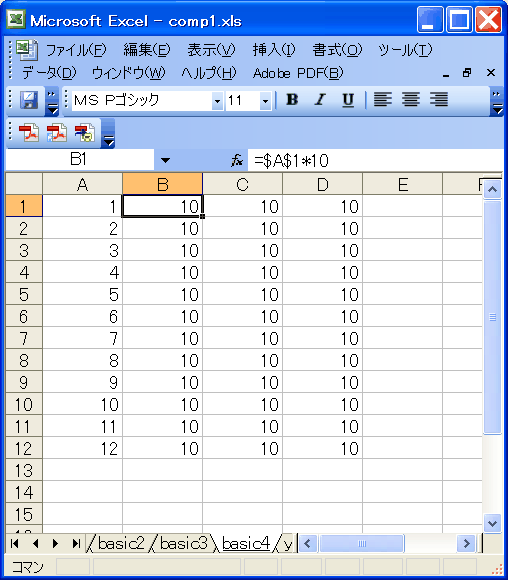
2:「D$3」型
「3」の前につけています。
| | A | B | C |
| 1 | 1 | =A$1*10 | =B$1*10 |
| 2 | =A1+1 | =A$1*10 | =B$1*10 |
| 3 | =A2+1 | =A$1*10 | =B$1*10 |
この場合は先ほどとは逆に、行方向(1〜)の指定は変わりません。
 |
| 行列(縦横)ともに=特定のセルを参照 |
3:「$D$3」型
| | A | B | C |
| 1 | 1 | =$A$1*10 | =$A$1*10 |
| 2 | =A1+1 | =$A$1*10 | =$A$1*10 |
| 3 | =A2+1 | =$A$1*10 | =$A$1*10 |
式をコピーしても、参照先は変わりません。
特定の定数を指定する場合などによく使います。
以上の「$」の指定も重要なテクニックですので、覚えておきましょう。
ここでは、簡単なグラフを書いてみます。
簡単とはいえ、工学部で表計算をつかう理由はデータの処理や数式の確認であって、使い道としては重要です。
普通のy=f(x)なグラフ
普通のy=f(x)型のグラフを書いてみます。
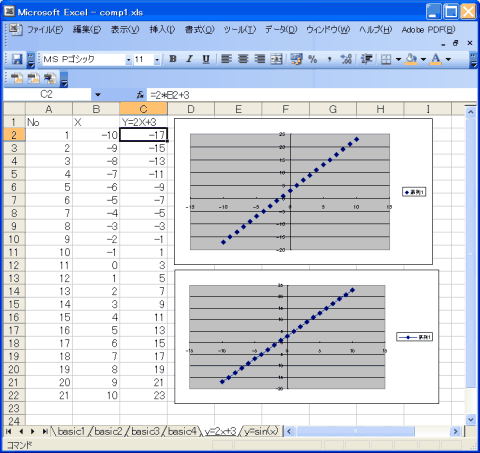 |
| y=2x+3のグラフ |
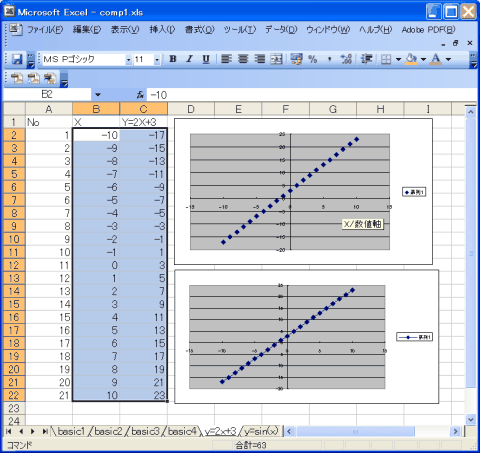 |
| 範囲の選択 |
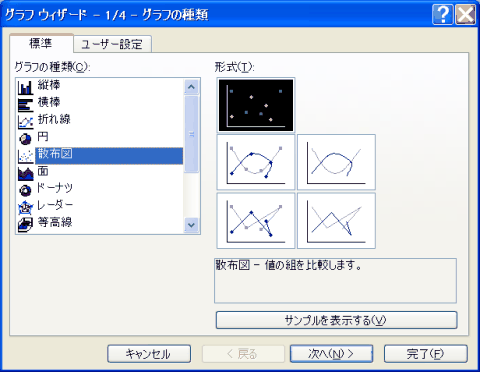 |
| グラフの種類選択 |
| | A | B | C |
| 1 | No | x | y |
| 2 | 1 | -10 | =2*B2+3 |
| 3 | =A1+1 | =B2+1 | ↓ |
| 4 | ↓ | ↓ | ↓ |
手順:
- A列に通し番号をつくっておく。
[A2]=1, [A3]=A2+1 を下コピー
表を必ず左上から使うわけではないため、「データがいくつか」「何番目か」をわかりやすくするために、つくっておくとよい。
- B列にXをつくる。
ここでは、−10〜10を1刻みでつくっておく。
[B2]=-10, [B3]=B2+1 (この+1が刻み)
これをコピーして合計21個にしておくと、+10までになる。
- C列にYをつくる。
[C2]=2*B2(すなわちX)+3, 下コピー
これで、B列のXに対応したYの値が求まる。
- B列C列の数値の範囲を選択する。
操作:B2にカーソル→Shift押しながらC22まで移動
すると、右図のように選択される。
※右図にはあるものの、まだ手元にグラフはない。
- グラフをつくる。
操作:メニュー→挿入→グラフ
すると右のようなダイアログボックスが表示されるので、 散布図 を選択する。
一般に、こういうグラフやデータを表すときは、散布図を使用する。その他は、どちらかというとビジネス的な使い道。
散布図には5種類形式があり、点のみ、点の有無、曲線でつなぐ、直線でつなぐが異なる。
本来、なにを意図して線を引くかを考えた上で形式を選ぶが、今回は点のみが妥当。
つながりをみたいときは「点+直線」「直線のみ」が無難。
中段の「曲線でつなぐ」は、グラフ化する点の配置によって思わぬ蛇行をすることがあるので要注意。
- 適当に移動する。
という手順で、y=2x+3のグラフができます。
これをやってみましょう。
さくっと終わって暇だ、という場合は、y=x*xなど、y=log(x)などその他の関数を試してみましょう。
21個の点でよければ、いまのままC列の式だけ差し替えれば、またB列のXの範囲や刻みを変えればすぐにグラフにも反映されます。
y=sin(x)のグラフ
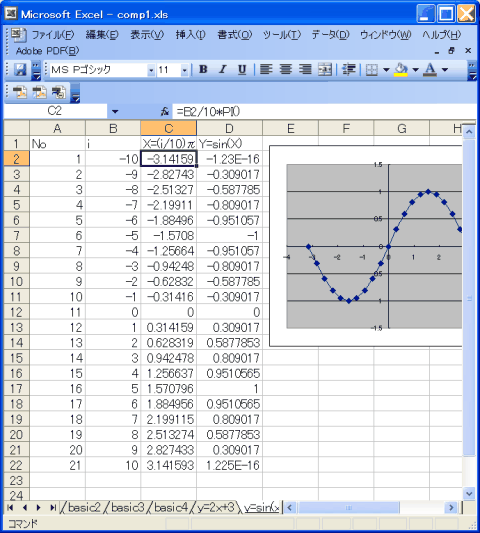 |
| y=sin(x)のグラフ |
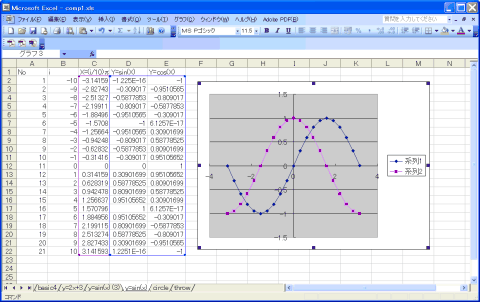 |
| y=sin(x)、cos(x)のグラフ |
もちろん、先ほどの方法で問題なくグラフにできます。
しかし、三角関数など、「π」が重要な横軸をもつグラフの場合は、x軸の刻みもπを元に作った方が見栄えがよくなることがあります。
そのほか、刻みを調整したい場合など、直接xを作るよりも「○番目のxを式で決める」という使い方が便利なことがあります。
そこで、右図ではB列に「i」という本来は必要のない値(中間変数、内部変数)をつくり、それでxを作っています。
| | A | B | C | D |
| 1 | No | i | x | y |
| 2 | 1 | 0 | =B2/10*PI() | =SIN(C2) |
| 3 | =A1+1 | =B2+1 | ↓ | ↓ |
| 4 | ↓ | ↓ | ↓ | ↓ |
ここで出てきた「Pi()」は「π」の値を常にもつ関数、「SIN()」文字通りsin関数です。
数表ができたら、同じようにグラフをつくってみてください。
これをやってみて、余裕がある場合は、SINの右に=COS(x)をつくってみましょう。
3列まとめて選択してグラフをつくると、同時に表示されます。
縦横比が重要なグラフ
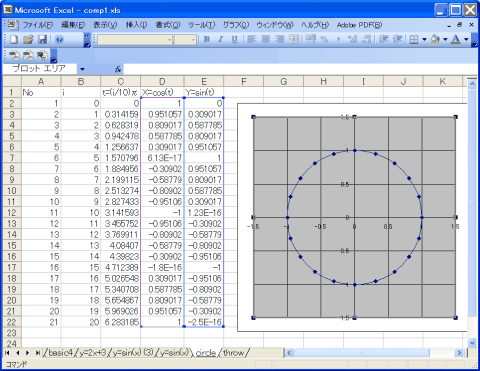 |
| x=cos(t), y=sin(t)のグラフ |
 |
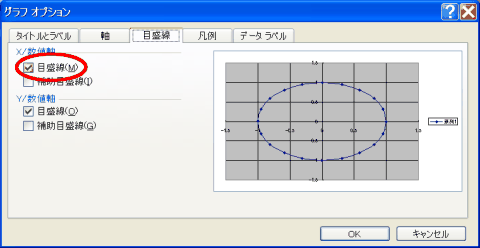
| グラフオプション |
 |
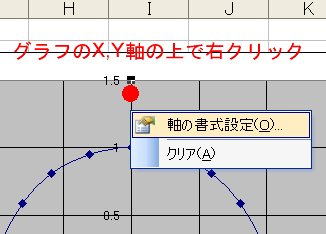
| 目盛線の設定 |
 |
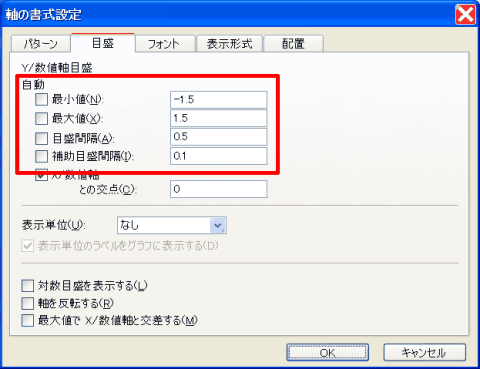
| 軸の書式設定 |
 |
| 軸の固定化 |
ここでは、
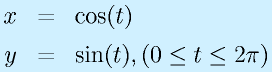
で表されるグラフを書いてみます。
これは
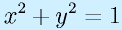
なので、半径1の円です。
| | A | B | C | D | E |
| 1 | No | i | t | x | y |
| 2 | 1 | 0 | =B2/10*PI() | =COS(C2) | =SIN(C2) |
| 3 | =A1+1 | =B2+1 | ↓ | ↓ | ↓ |
| 4 | ↓ | ↓ | ↓ | ↓ | ↓ |
数表の作り方は似ています。先ほどのグラフでxだったところが、tに代わり、x、yがCOS, SINになっただけです。
ただ、そのまま、xyを選んでグラフにすると、楕円が表示されます。
座標軸をみると、ちゃんと1を通っていますが、座標軸の比率が1:1でないため、楕円になります。
こういう「平面であること」「形をみたい」が重要なグラフの場合、この軸比が重要です。
そこで、調整します。
単純には、グラフそのものサイズを変えてしまい、見た目で軸の長さが同じになるようにします。
ただ、x軸は目盛だけ、y軸は線と、そもそも見た目が異なり、調整しにくいので、統一します。
右の2つめの図のように、グラフのブロック内のグラフの書かれていない白地のところで右クリックをします。
そのなかに「グラフオプション」があるので選びます。
そのなかの「目盛線」タブを選んで、x軸の目盛線にもチェックをいれます。
今回は、これで目盛線が正方形になるようにグラフのサイズを修正すればOKです。
しかし、表示する関数によっては、そもそも、縦軸、横軸の目盛の間隔が異なったり、値を変えたときにかってに軸の目盛がかわったりして「おせっかい」に悩まされることがあります。
この場合、軸を固定します。
右4番目の図のように、グラフの軸のうえで右クリックすると、「軸の書式設定」が現れます。
ここで、「目盛」タブをひらき、「自動」のチェックを外し、右に好きな値を設定します。
さしあたり、X軸とY軸で「目盛間隔」が一致していればよいでしょう。
以上のような操作により、関数や数値で規定されたものの形が、わかりやすく図示できるようになります。
これは特に、計算で設計したり、シミュレーション結果をグラフで表示するときに、座標として「xy」が出てくるならば必須の操作といえます。
演習課題
![斜方投射 (v0=5, θ=45[deg]の場合)](fig/thumbFH_comp1_g4.gif) |
| 斜方投射 (v0=5, θ=45[deg]の場合) |
次回(10月12日)の講義開始時点 までに以下のグラフを作成し、「r01_(学生番号).xls」というファイル名で保存しておいてください。
講義冒頭で回収します(課題提出の試験をかねて)。
物体を初速度 v0[m/s]で水平から上方に角度θの方向に打ち出すと、放物運動をします。
空気抵抗を無視すると
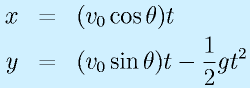
という軌道を描きます。
これを時間間隔 0.04[s]ごとに、計算し、グラフにしてください。
計算の数はy=0になるところ(地面に落ちるところ)までは含む程度、適当に決めてください。
その際、
- 初速は「学生番号の100の位(1か2)+4」→5か6
- 打ち出し角度は「学生番号の1の位(0〜9)+40」→40〜49[deg]
注意:cos, sinはラジアン単位なので、deg→radの変換をする (/360*2*Pi()など)
- g=9.8とする
とします。
右図は参考です。こういう感じにしてください。
到達度チェック
- それらしいx、yが計算できている&グラフがつくれた
- グラフの縦横比がだいじょうぶ
- +α:v0, θ, g を式に直接ではなく、絶対参照を使って組み込み、調整できるようにする
- +β:そのほかに、複数のθでの軌道を比較できるようにしてみた
数列とΣと+=
コンピュータで処理する対象は、上の例のように、基本的には数字たくさんです。
大量の数値といっても、だいたいは「同じ性質」「同じ意味」をもった数値のセットです。
たとえば、直前の放物運動は「時刻t」「座標x」「座標y」が連続的にあります。
(他に初速のような単品の数値は、全体を調整する値:パラメータとして存在する)
このような数値の連なりが「数列」です。
数列というと、高校で習う漸化式がどうこう、等比数列、等差数列などがありますが、あれは特殊な部類で、我々が使うものは「実際のデータ」としての数列が一般的です。
さて、その数列の計算で、ここまでの例は数列の個々の数値から別の数値を計算し、別の数列を1対1で作り出すというものでしたが、数列ごとに計算が必要な場合があります。
その例が「合計」とか「平均」のたぐいです。
こういった、数列の計算について、今後使う表記を明示しておきます。
](eqn/spreadsheet.bhtml.eqn4.gif)
数列は「同じ性質」のものが複数ある、という考えのため、文字で表すときはすべてを同じ文字で、ただし「添え字」をつけて表記します(添え字は整数で、一般に正です)。
数学的には前者の下付け文字で表すことが一般ですが、コンピュータのプログラミング言語での表記で一般的な「[]」による表記もよく使われます。
添え字はたいていは連番ですが、1から始まる場合、ゼロから始まる場合など定まってはいません。
不特定の一つを表すときに"i"などの文字を使います。
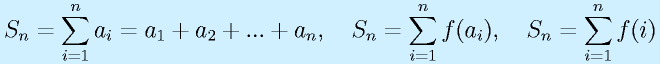
数列の合計を表すときには、記号Σを使用します。
Σの下と上には、「どこからどこまで足すか」が示されます。
下の「i=1」は「iを順番に変えていくこと」「iを1から順に増やすこと」を示しています。
上の「n」は「(下で指定されているiを)nまで増やすこと」を示します。
一つ目の例は、併せて「数列aiをa1からanまで全部加える」という意味になります。
二つ目、三つ目の例も1〜nですが、「aiの関数」(たとえば、ai×5+3みたいな)の和、そもそも数列自体をその場でiをもとに関数で作ってしまう場合(例:2i-1はi=1,2,3に対して1,3,5となり奇数になる)です。
ともかく、Σの下でどの文字で順番を表すか、下と上でどこからどこまでかを明示します。
なお、「aiを1からnまで加えたもの」は新たに「s1=a1, s2=a1+a2...」と別の数列になります。
たいてい必要なのは「n個の合計」とかですが。
※下にiとだけ書くような場合があり、その場合は具体的な計算ではなく、「合計をもとめるという発想」のみを主張。
実際の使い方をあげると、
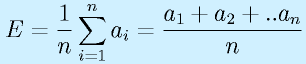
はn個の数値a1〜anの平均の計算を表します。
さて、実際に合計値を求めるには、どうすればいいかというと、
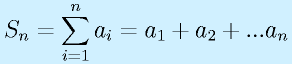
をいきなり数式としてコンピュータに与えて計算するほか、
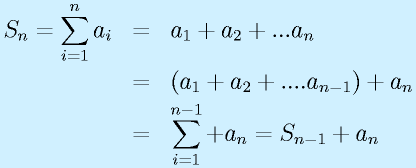
と書き換えることで、
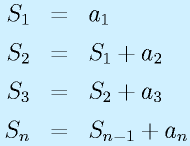
となり、最初以外を
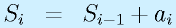
という1種類の式の繰り返しに置き換えることができます。
最初の直接的な式は「100個の合計」といわれたら100項入力しなければならず、苦痛でありミスも起きます。
しかし、書き換えた方法は式は1本、あとはコンピュータに「100回繰り返せ」というだけで、同じ式で1000回でも計算できます。「繰り返す」はコンピュータが得意な方法なので、こういう書き換えは非常に重要です。
実際、「プログラムを作る」という場合、させたいことをいかに「単純な指示の繰り返し」に置き換えられるかが、実際の作業を簡単に、かつトラブルなくこなすことにつながります。
この計算をもう少し見直します。
最終的にSnだけ必要という場合、途中のSiはいりません。ので、これを数列として「とっておく」必要はありません。
そこで
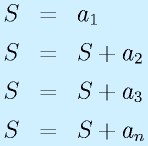
と書き換えてしまいます。その繰り返す数式
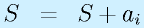
は等式としてみたときには明らかに変ですが、
「電卓と表計算とプログラム」のところで説明した「代入の=」と考えれば、
「Sにaiを加えてものをSに入れる」
という意味です。が、これは普段の言葉では単純に、
「Sにaiを加える」
といいます。数学的には特別の表記はありませんが、コンピュータの世界ではしばしば、
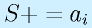
と「+=」を使います。(−=、*=、/=なども同様に存在)
表計算での合計の求め方
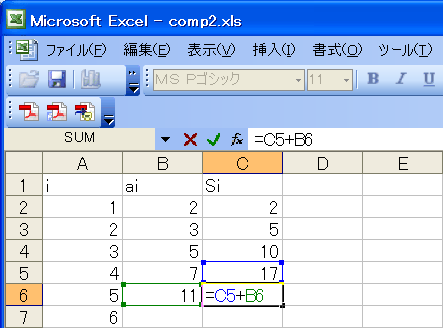 |
| Si=S(i-1)+ai |
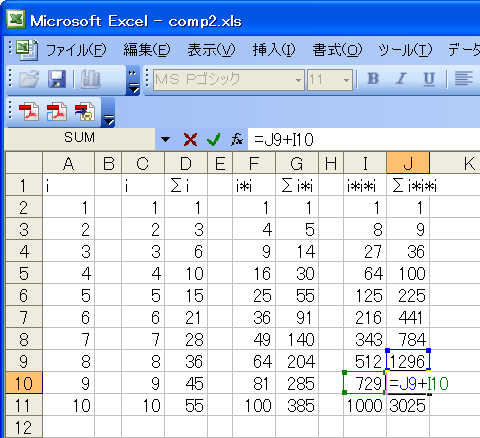 |
| i, i*i, i*i*iを加えていく |
表計算ソフトでの合計の求め方は、ほぼ、上の説明をそのまま、シート上に作ります。
| | A | B | C | D |
| 1 | i | ai | Si | |
| 2 | 1 | (a1の値) | =B2(a1相当) | |
| 3 | =A2+1 | (a2の値) | =C2(S1相当)+B3(a2相当) | |
| 4 | ↓ | (a3の値) | ↓ | |
aiの値は実際のデータの場合もあれば、何らかのiによる数値の場合もあるでしょう。
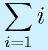
(1から順に足していく)
という場合は、
| | A | B | C | D |
| 1 | i | ai | Si | |
| 2 | 1 | =A2 | =B2(=a1) | |
| 3 | =A2+1 | =A3 | =C2(=S1)+B3(a2) | |
| 4 | ↓ | ↓ | ↓ | |
で、式をコピーした数だけ合計が求まります。aiが10のところ(11行目)には、Siは55(=1+2+..10)になっているはずです。
これをもとに、
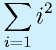 (1から順に2乗で足していく)
(1から順に2乗で足していく)
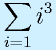 (1から順に3乗で足していく)
(1から順に3乗で足していく)
を試してみましょう。
人によっては「1+...n」が「n(n+1)/2」になることを覚えているかもしれませんが、忘れてしまっても、表計算ソフトがあれば、数百くらいまでは式のコピーで一気にいけます。
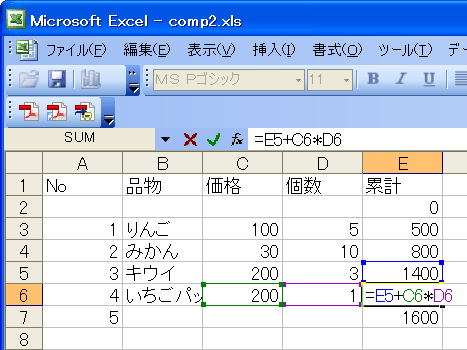 |
| お買い物計算 |
おまけ:買い物計算
| | A | B | C | D | E |
| 1 | No | 品物 | 価格 | 個数 | 累計 |
| 2 | | | | | 0 |
| 3 | 1 | りんご | 100 | 5 | =E2+C3*D3 |
| 4 | =A3+1 | みかん | 30 | 10 | ↓ |
| 5 | ↓ | キウイ | 200 | 3 | ↓ |
2行目の項目を「予算」にしてE2に予算額を、E3以降の数式を「=E2-C3*D3」にするとお金の減り具合がわかります。
高校生の頃からそれでお小遣い帳を大学院終わるくらいまでつけてました(笑)。
(途中で通帳連動にしたり、消費税対応にしたりしてどんどん(ファイルが)肥大化)
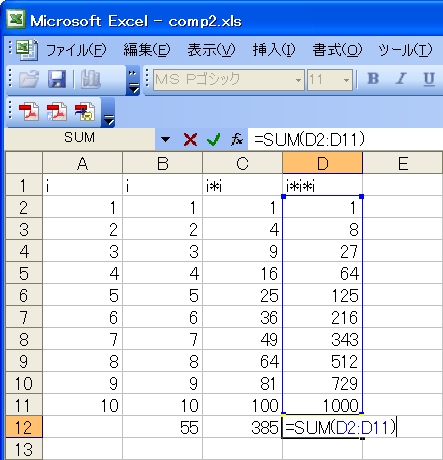 |
| i,i*i,i*i*iをsum |
もう一つ、表計算ソフトで合計を求めるだけなら、便利なものがあります。
=sum(左上セル:右下セル) 例:=sum(C3:C7)
と書くと、長方形領域のセルの合計値が求まります(普通は縦1列とか横1行の範囲だけですが)。単に決まった数のデータの合計だけを求めたいという場合に、つかえます。
| | A | B | C | D |
| 1 | i | i | i*i | i*i*i |
| 2 | 1 | =A2 | =A2*A2 | =A2*A2*A2 |
| 3 | =A2+1 | ↓ | ↓ | ↓ |
| 4 | ↓ | ↓ | ↓ | ↓ |
| : | : | : | : | ↓ |
| 11 | ↓(=A10+1) | ↓(=A11) | ↓(=A11*A11) | ↓(=A11*A11*A11) |
| 12 | | =sum(B2:B11) | → | →(=sum(D2:D11) |
もちろん、sumを使ったセルもコピーでき、「$の規則」もそのまま働きます。
※右コピー:範囲指定でCtrl-R(メニュー→編集→フィル→右, Alt+E-I-R)
最小2乗法
合計計算の最後に最小2乗法の計算をしてみます。
最小2乗法は、
(xi,yi)の組のデータから y=ax+bの関係を探す
などを行う計算法です。3年生の学生実験の最初にも原理を含めてやりますが、ここでは原理抜きに計算だけしてみましょう。
具体的には、以下の計算をします。
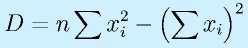
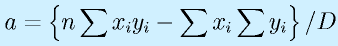
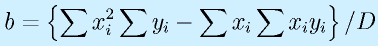
ただし、nはデータの個数で、すべてのΣは「対象となるすべてのデータに対して」なので、略しています。
(※Dは最終的には不要な値。ただ、a,bで共通に分母になるのであえて別に計算した方がわかりやすい)。
この式を計算するためには、
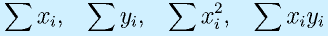
の4つの合計値が必要です。
そこで、表計算で計算する方針としては、
- データは縦方向に並べる。
- xi,yiの組を用意する。
- その横にxi*xiとxi*yiを計算する
- sum()をつかって合計を求める
- D,a,bを求める。
とします。
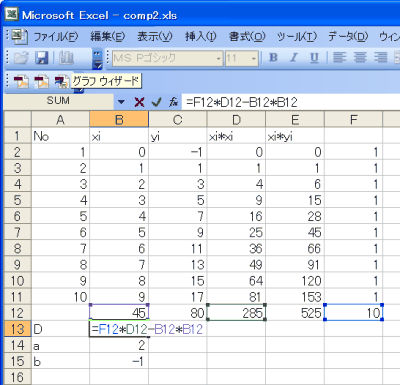 |
| 最小二乗法の計算例 |
| | A | B | C | D | E | F |
| 1 | No | xi | yi | xi*xi | xi*yi | |
| 2 | 1 | x1の値 | y1の値 | =B2*B2 | =B2*C2 | 1 |
| 3 | =A2+1 | x2の値 | y2の値 | ↓ | ↓ | ↓ |
| 4 | ↓ | : | : | ↓ | ↓ | ↓ |
| : | : | : | : | : | : | : |
| 11 | (n) | xnの値 | ynの値 | ↓(=xn*xn) | ↓(=xn*yn) | 1 |
| 12 | | =sum(B2:B11) | → | → | → | →(=sum(F2:F11) |
| 13 | D | ※1 | | | | |
| 14 | a | ※2 | | | | |
| 15 | b | ※3 | | | | |
※1=F12*D12-B12*B12
※2=(F12*E12-B12*C12)/B13
※3=(D12*C12-B12*E12)/B13
最後の計算式が多少やっかいですが、大部分は式のコピーですみます。
基本的に、先の数式、手順の通りですが、F列に「1」だけを足し続ける変な列があります。これは
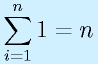
という当たり前の計算をしています。
この妙な式には意味があります。
多くの場合、最小2乗法を使おうという場合はデータの数は予めわからないことがあり、実験の結果などとして、n個のデータが得られます。
そこで、「n」を求めるため、与えられるxやyと同じ数だけ「1を加える」ことでnを得ています。
同じnはこの計算表ではA11のところにも現れていますのでこれを使うことも可能ですが、D,a,bの計算で一つだけ11行の数字を使うよりは、すべて12行目の値だけで計算できた方が美しいと思いませんか?
実際問題としては、データを追加したりするときのリスクは、この方法で求めたnのほうが安全と考えられます。
演習課題
 |
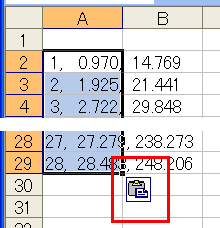
| 数値の範囲を選択する。(マウスでドラッグ) |
 |
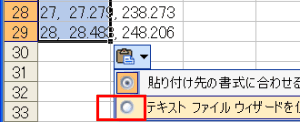
| Excelに貼り付ける |
 |
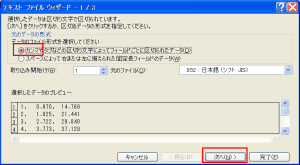
| 右下のアイコンをクリック→テキスト... |
 |
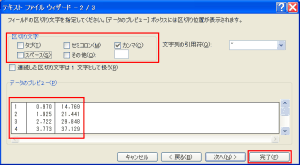
| カンマやタブ区切りを選択 |
 |
| カンマのみを選択 |
 |
| 元になる数表の貼り付け完了 |
最小二乗法実習データのページから、数値データを得て、これに最小二乗法の計算をして、a,bを求めてみてください。
手順:
- 最小二乗法実習データのページで「学生番号の下三桁を半角数字で」入力し「生成」ボタンを押す。
- 枠内に出てきた結果の「1,...」〜「2?,...」(人によってデータの数は変わります、たぶん)の範囲をマウスで選択してCtrl-C(メニュー→編集→コピー)。
- Excelを開き、A2セルのところでCtrl-V(貼り付け)。
- 貼り付けたところの右下にでる小さなアイコンを左クリックし、「テキストファイルウイザードを使用」をクリック。
- 「元データの形式」で「カンマやタブ...」を選んで「次へ」
- 「区切り文字」で「カンマ」のみにチェックを入れる(最初スペースに入っているのは外す)
「データのプレビュー」で数値の間に線が入っていることを確認。
- 「完了」を押す→数値が入る。
- 適宜、xi*xi, xi*yiを加え、D,a,bを計算する。
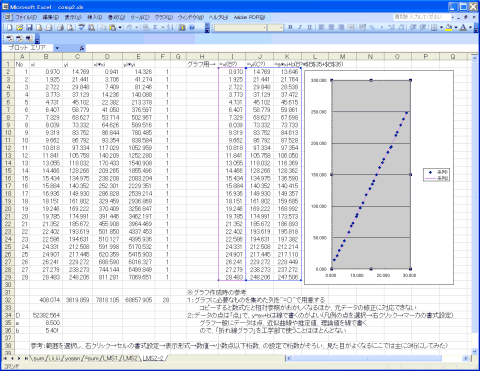
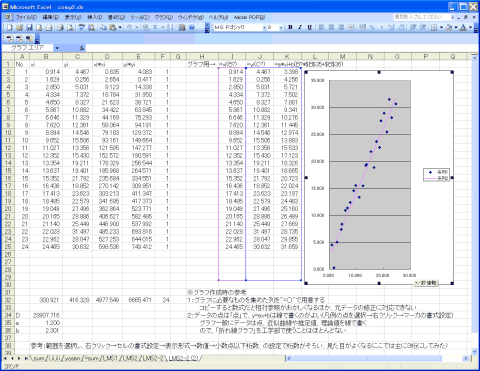
- +α:xi,yiについて、グラフをつくってみる。求めたa,bはそれらしい値かみてみる。
なお、上の手順3のアイコンが出ずに張り付いた場合、貼り付けたセルの範囲を選択し、
メニュー→データ→区切り位置
でも同じ操作ができます。また、同じ操作を繰り返しているとそのうちExcelが学習して、数字をうまく入れてくれるようになることがあります。
できた人は ファイル名 "r02_学生番号.xls"(半角)で保存の上、課題番号r02でレポート提出。期限10/26日講義前。
(ただし、講義の進捗状況により、課題としない場合もあります:講義で通知)
ここまで終わって時間が余るという場合は、345,456,567あたりのデータも試してみましょう(提出は自分の学生番号3桁で)。
そのときに、数式を入力し直すのではなく、既存の最小二乗法計算シートを活用する方法を考えてみましょう。
例:(854と123の場合、+αのグラフ付き)















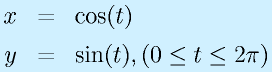
![斜方投射 (v0=5, θ=45[deg]の場合)](fig/thumbFH_comp1_g4.gif)
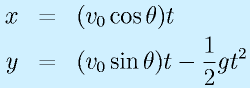
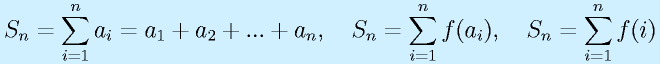
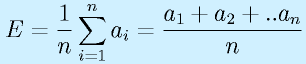
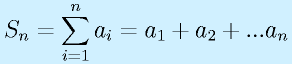
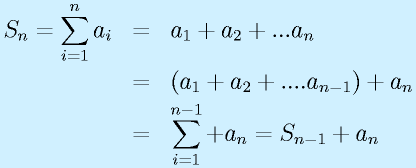
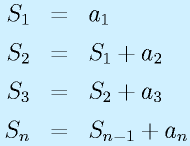
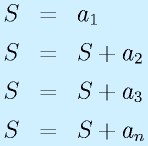


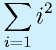 (1から順に2乗で足していく)
(1から順に2乗で足していく)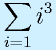 (1から順に3乗で足していく)
(1から順に3乗で足していく)