ディジタル制御の基礎
[| ]
最終更新: 2011/02/10 19:33:01
ディジタル制御
制御とディジタル
これまで制御工学Iを含めて、いろいろな制御を扱ってきました。
しかし、理論面のみで実装面(実際にものとして作ること)については触れられてこなかったと思います。
古典制御の簡単な物は、電子回路によって実装することができます。たとえばその典型例であるPID制御は比例は定数倍増幅アンプ、微分、積分もそれぞれ電子回路があります。
→メカトロニクス:アナログ回路の基礎
しかし、今日では古典制御も含めて、コンピュータ制御とすることが一般的です。アナログ回路の場合は、一度作ると変更が難しく、精度管理が難しく、実装も面倒であり、非線形制御は原則としてできないのに対して、マイコンなどのコンピュータを使用するとこれらの欠点の多くが解消されます。
では、コンピュータで制御するとすべてが丸く収まるかというと、ディジタル特有の問題が発生します。
そこそこの性能で作るならあまりトラブルにはなりにくいのですが、思わぬ落とし穴になることもあります。
実際に制御系を実装するにあたり、ディジタル制御について学んでおきましょう。
コンピュータ制御システム
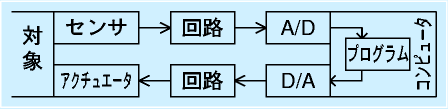 右図にコンピュータ制御システムの構成例を示します。
右図にコンピュータ制御システムの構成例を示します。
対象にはセンサを取り付け、状態を電気信号に変換します。これを回路で適当な大きさの電圧信号にAD変換器(AD converter, A/D)によってディジタル値に変換し、コンピュータのプログラムでこの値を処理して制御則を実行し、操作量を算出したらDA変換器(DA converter, D/A)によってアナログ値に変換し、回路で処理して、モータなどのアクチュエータを操作します。
(最近は操作系はD/Aを使わずすべてディジタルで済ませることが一般的です。オーディオやビデオ信号はアナログが主流ですが、一部にフルディジタルなものが出てきています)
ここではこういったシステムで起こりうる現象を見ていきます。
離 散
ディジタル化するときに、必ずつきまとうのが「離散」という現象です。離散には大きく二つあり、
- 値の離散:連続的な入力に対して、その変換値がとびとびになる
- 時間の離散:値の取り込みや処理には時間がかかるため、時間がとびとびになる
といった現象がおきます。
値の離散
 コンピュータに値を取り込む際には、AD変換器が用いられます。
これは入力電圧をたとえば0〜255などの整数に置き換える回路です。
コンピュータに値を取り込む際には、AD変換器が用いられます。
これは入力電圧をたとえば0〜255などの整数に置き換える回路です。
入力電圧は、段階的に、隙間無く存在しますが、変換された値は、そのとりうる値の種類が限られています。
その結果、ある入力の値の範囲に対して、ディジタル側の1つの数字が割り当てられることになります。
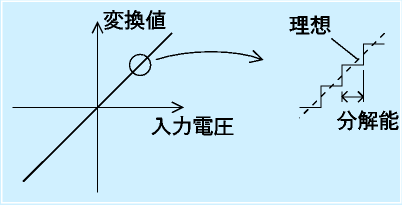
それを図示したのが右図です。
AD変換器は大局的にみれば、入力電圧に比例した、もしくは直線的な関係の値を出力します。しかし、その一部を拡大してみると、その変換関数がギザギザになっています。ある電圧範囲に対して、変換値は一つで、次の範囲になると変換値は飛びます。
これを値の量子化といいます。
変換値1に対する電圧の範囲をAD変換の分解能といいます。これはAD変換器の性能と関係があって、
| 8bit A/D | 0.4%FS | ±10V→78mV刻み |
| 12bit A/D | 0.024%FS | ±10V→4.9mV刻み |
| 16bit A/D | 1.5e-5FS | ±10V→0.31mV刻み |
FS: フルスケール
となります。8ビットだとちょっと粗い感じがしますが、12ビットもあると、普通はたります。16より分解能が悪いのは明らかですが、逆に、4.9mVにもなると、この性能を活かせる、直前までの電子回路を作ることがやっかいです。
実際に選定するときは、このあたりも勘案します。
時間の離散
 本来、電気信号は時間的にも連続です。しかし、AD変換器は変換するのに多少の時間がかかります。また、それをコンピュータで処理して出力する場合もかならず時間を要します。
本来、電気信号は時間的にも連続です。しかし、AD変換器は変換するのに多少の時間がかかります。また、それをコンピュータで処理して出力する場合もかならず時間を要します。
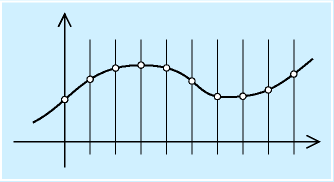
そのため、コンピュータで扱われる信号は、右図のように時間的に隙間があきます。
処理などは時間変動があり得ますが、一般に、値の取得=サンプリング(標本化)は一定の時間間隔で行います(必要なら敢えて待ち時間を入れるなど)。
このサンプリングの間隔をサンプリング周期Ts、周波数をサンプリング周波数fs(=1/Ts)といいます。
このサンプリングされた値を記述するため、以下の数式を用います。
とかけます。ここで、t0は時刻の適当な基準点、kは信号系列の番号です。値がとびとびなので、これは整数になります。
なお、ここから先、先ほどの値の離散はちょっと棚上げしておいて(十分な分解能、精度があると仮定)、時間の離散に関わる部分を確認していきます。
サンプリングにともなう問題
(1)量子化誤差
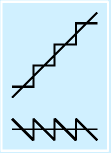 上でも触れたように、AD変換を行う際には、入力のある範囲は一つの値にまとめられ、結果的にADの入力と変換値の関係は階段状になります。これは期待される直線的な対応とはノコギリ状の誤差が発生します。
上でも触れたように、AD変換を行う際には、入力のある範囲は一つの値にまとめられ、結果的にADの入力と変換値の関係は階段状になります。これは期待される直線的な対応とはノコギリ状の誤差が発生します。
この誤差は、もっとも条件がいいときで、分解能の半分になります(ステップの前後で大きさが等しいとした場合)。
AD変換器には実際には量子化誤差の他にも誤差があって、そもそも大局的に見ても直線ではない誤差、局所的に単調増加しない誤差などがあり、選定時にはその辺りの検討も必要です。ビット数、変換速度だけではありません。
(2)サンプリング定理
 サンプリングに伴う、もっとも有名な問題がサンプリング定理と呼ばれる、信号の変化とサンプリング時間間隔の関係に由来する問題です。
サンプリングに伴う、もっとも有名な問題がサンプリング定理と呼ばれる、信号の変化とサンプリング時間間隔の関係に由来する問題です。
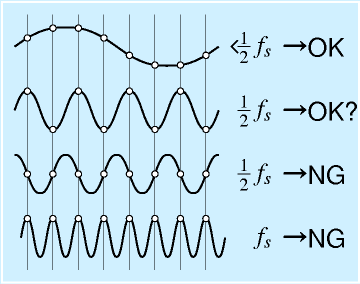
右図のように、正弦波状の周期的な信号をサンプリングするとします。図で縦線はサンプリングのタイミングを表します。
一番上の例、8サンプリングで1周期程度の場合(=サンプリング周波数の1/8)、波形の線を見ずに、サンプル点の白丸だけを見ても波形の形はほぼ完全に得られています(周期、位相、振幅)。
次に、2サンプリングで1周期の場合として、2段目の波形は形が三角っぽくなるものの振幅や周期が保存されていますが、同じ周波数でも3段目では完全に平らになってしまい、波形がなくなっています。つまり、サンプリング周波数の半分辺りになると、もう波形を正しく取得できなくなることがわかります。
サンプリング周波数と一致すると、どこでとっても完全に平らになってしまいます。
以上のような性質をのべたのがサンプリング定理で、
- サンプリング周波数の1/2までの信号しか取得できない。
- 取得したい信号の2倍以上の周波数でサンプリングしなければならない。
とされています。ただし、1/2の直前になると、サンプリング後にいろいろ工夫しないともう復元できないので、形状まで必要な場合、最低で取得したい信号の4倍、余裕を見て10倍程度が必要とされています。
なお、速ければいいっていうものでもありません。速いほど、大量にデータがでてくるため、その保存などの問題がおきます。
ちなみに、ディジタルオーディオ(CDなど)ではサンプリング周波数が40kHz近辺にあることが多いのですが、これは、人間の耳が20kHz程度まで聞くことができるとされていることから決められた周波数です。
 サンプリングに関連して、もう一つの現象があります。
サンプリングしているところに、1/2を越える信号を入れてしまうとどうなるか、という問題です。
サンプリングに関連して、もう一つの現象があります。
サンプリングしているところに、1/2を越える信号を入れてしまうとどうなるか、という問題です。
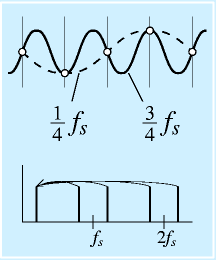
たとえば、周波数fsでサンプリングしているところに、(3/4)fsの信号を入れてみます。これは1サンプル区間に、3/4周期入るような波です。
右図のように、またサンプル点に丸をつけてみると、その丸の並びから、別の線が見えてきます。具体的には、上下が逆になっていますが、(1/4)fsの波です。
この例のように調べていくと、サンプリング周波数fsのところに、周波数f(0.5fs<f<fs)の信号を入れると、サンプリングされた信号は、周波数(fs-f)の信号に化けます。加えて、fs
周波数のグラフを、0.5fsごとに折り曲げて畳んだように重なる位置がでるためか、折り返し歪みと呼ばれます。または、エイリアシングと呼ばれます。
この現象はテレビなどでよくみられます。西部劇(最近あまり見掛けないですが)で馬車の車輪のスポークが、ゆっくり走っているときはちゃんと回って見えるのに、加速するとなぜか逆回転したり、止まって見えたりします。また、自動車のコマーシャルでも、ホイールを良く見ていると同じように逆回転したり止まって見えることがあります。これは、周期的に回転している部品を、カメラでサンプリング(映画だと秒24コマ、ビデオカメラだと30もしくは60コマ)したことで起きた、折り返し歪みです。
また、(インバーターではない安い)蛍光灯の下で羽を良く見ながら扇風機のスイッチをいれると、羽の上にゆっくりまわる模様が見えることがあります。これは蛍光灯の光が点滅(50Hz*2で100Hz)していて、それが反射したものを観測しているために、そう見えると考えられます。これを積極的に利用したものにストロボスコープとか、それに類する回転計があります。点滅する光をあてることで、本来高速で回転している歯車の静止画像や低速回転を撮影することができます。また、止まって見えるように周波数を調整すれば、それが対象の回転数になります。
(3)出力側の問題
 一方、出力側にも同じような問題があります。
一方、出力側にも同じような問題があります。
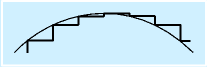
出力にもサンプリング間隔があり、ある程度間隔をおいて出力するため、出力が階段状になります。
それほど問題になることはないのですが、これは本来意図しない周波数成分が、出力にまじることになります。具体的には、一番大きいのはサンプリング周波数fsの成分で、その整数倍が存在することが一般的です。
サンプリング周波数が低い場合、音を再生するとなにか「ぴー」とか「ひー」とか聞こえるかも知れません。
(4)対応策
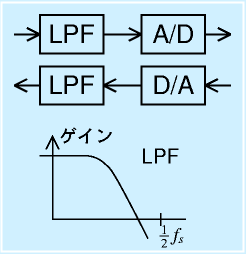 これらの問題に対応するため、一般に、AD、DA変換の前後には、アナログ回路のローパスフィルタ(低い周波数のみを通すフィルタ)をいれます。これにより、
これらの問題に対応するため、一般に、AD、DA変換の前後には、アナログ回路のローパスフィルタ(低い周波数のみを通すフィルタ)をいれます。これにより、
- サンプリング周波数の半分以上の成分が入力されないようにする
- 出力に混じった、サンプリング周波数より高い成分を除去する
という対策になります。このフィルタのことを「アンチエイリアシングフィルタ」といいます。
しかし、アナログフィルタはある周波数ですぱっと切ることはできないため、サンプリング周波数の半分ぎりぎりまで信号を通すといったことはできません。この場合はサンプリング周波数をあげることになります。
なお、オーディオ機器で「オーバーサンプリング」という用語があります。これは、本来40kHzくらいでサンプリングされた信号を、一旦、4倍、8倍などの周波数に補間しながら上げて、より急峻なフィルタを作りやすいディジタルフィルタで補間した際にできた不要な成分をすぱっと落して、4、8倍の周波数でDAしてやることで、ローパスフィルタの特性を穏やかに為つつ、元信号をギリギリまで再生するための方式です。
(5)制御とのかねあい
もちろん、制御にもこれらの問題は付きまといます。分解能については、使うセンサやアクチュエータ、およびそれらの周辺の回路と相談することになります。サンプリング周波数については、制御対象の応答性(固有振動数=固有値虚部)やセンサの応答周波数などをもとに決めることになります。
制御のサンプリング周波数が低いと、当然制御がうまく行かないケースが出てきます。
しかし、やたらと上げると、この次の微分積分で問題がでることがあります。
離散時間における積分と微分
信号を処理する場合や制御において、積分や微分はたびたび必要になります。
センサ信号を処理する場合、たとえば、位置のセンサの出力を微分すれば速度が得られ、角速度のセンサを積分すれば角度が得られます。このように、本来ほしいセンサが無い場合に既存のセンサの信号を加工したり、2種類以上の信号が必要なときにそれをつくり出すことがあります。
古典制御の代表格であるPID制御において、Iは積分、Dは微分が必要です。
ところが、積分や微分はそもそも、変化が連続しているときに、極限の微少時間での変化や積み重ねを演算するため、サンプリングにより時間が離散化してしまうと、そもそも定義通の演算ができなくなります。
そこで、その代替計算を行います。
具体的には、それぞれの定義に立ち戻り、Δt→0をしないだけです。
(1)積分
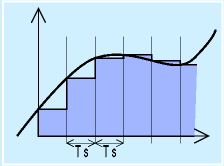 そもそも、積分の概念は、右図のように、なんらかの関数があったときに、それがゼロと囲む範囲の面積をもとめるように、短冊状に切り、各々の短冊の面積を積算していく計算です。
本来の積分では、短冊の幅を極限まで小さくすることで、短冊の端と対象関数の形状の差を限りなくゼロに近づけています。
そもそも、積分の概念は、右図のように、なんらかの関数があったときに、それがゼロと囲む範囲の面積をもとめるように、短冊状に切り、各々の短冊の面積を積算していく計算です。
本来の積分では、短冊の幅を極限まで小さくすることで、短冊の端と対象関数の形状の差を限りなくゼロに近づけています。
離散時間での積分は、この極限をとるという操作をしないだけです。もちろん、右図にも出ているように、本来の積分値に足りないところやはみだすところが出ていますが、長い目でみれば適当に平均化されるというスタンスです。
具体的には、系列[k]における積分値I[k]を
![I[k]=\sum^k_i u[i]T_s](eqn/digicont.bhtml.eqn4.gif)
で求めます。u[i]は積分する対象の系列、Tsはサンプリング周期です。
一般に、「一定周期でサンプリングする」と上でのべましたが、それは、このTsを定数にできる、という意味合いもあります。
なお、数値積分の公式として、台形公式やルンゲクッタ法などがありますが、制御用という観点では、計算量が増大するわりには、それほど性能も改善せず、あまりお得ではありません(特にルンゲクッタはサンプルの中間の値も必要だったりする)。
(2)微分(差分)
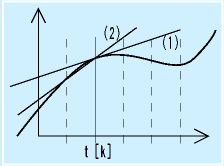 本来の微分は、ある時点での関数の変化率を求めます。定義では、狭い時間間隔の2点での関数値を求め、その傾きを出し、その上で、時間間隔を極限まで狭めます。(図(1))
本来の微分は、ある時点での関数の変化率を求めます。定義では、狭い時間間隔の2点での関数値を求め、その傾きを出し、その上で、時間間隔を極限まで狭めます。(図(1))
離散時間の微分は差分ともよばれ、極限を求めません。
具体的には、微分値D[k]を
![D[k]=\frac{u[k]-u[k-1]}{T_s}](eqn/digicont.bhtml.eqn5.gif)
と、現時点での値と、1回前の値の差をとり、これをサンプリング周期で割ります。(図(2))
式に、
![D[k]=\frac{u[k+1]-u[k-1]}{2T_s}](eqn/digicont.bhtml.eqn6.gif)
を使えると、精度が上がりますが、u[k+1]は未来の値であるため、制御中には使えません。オフラインでデータ処理する場合などには、この値が使えます。
(u[k]-u[k-2]を使うと遅れが問題になる)
|
(3)PID制御の例
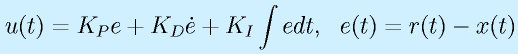
を離散時間で書き換えると、
![u[k+1]=K_Pe[k]+K_D(e[k]-e[k-1])/T_s+K_IT_s\sum e[k]](eqn/digicont.bhtml.eqn8.gif)
となります。
なお、サンプリング周波数が固定であれば、TsをKDとKIをそれぞれ含めてしまうことができます。
(4)補足:サンプリング周波数の検討
サンプリング周波数を必要以上にあげると、微分値が極端になり、制御に悪影響をおよぼすことがあり、その場合はいろいろと信号処理の対策が必要になることがあります。
たとえば、
| 10 | | 11 | | 11 | | 12 | | 12 | | 13 | | 13 | | 14 | | 14 | | 15 |
| 1 | | 0 | | 1 | | 0 | | 1 | | 0 | | 1 | | 0 | | 1 | |
| 10 | | 15 |
| 5/10=0.5 | |
のように、2秒に1回数字が増えるようなケースで、1秒ごとにサンプリングするとその微分値は0と1を繰り返します。
しかし、10秒後とのサンプリングにすると、微分値は0.5になります。どちらが良いかは時と場合によりますが、制御にDがある場合、あまり極端な微分値の変化は制御を不安定化します。
もちろん、サンプリング周波数を極端にあげると、AD変換器や、CPUの速度も必要になるので、最低限ほどほど、が重要です。
Z変換
連続時間の動的システムを解析するために、ラプラス変換というものを使ってきました。
同じように、離散なシステムを解析するためにZ変換というものが使われています。
この節では、Z変換の定義と、それを用いた伝達関数表現とを扱います。
Z変換
Z変換の概念:
入力信号 u(t)を周期Tでサンプリングした
![u[k]=u(kT)](eqn/digicont.bhtml.eqn101.gif)
に対して、
![z\,u[k]=u[k+1]](eqn/digicont.bhtml.eqn102.gif)
となるような変換を考えます。ここで、zの意味は、「系列u[k]を一つ進める」ことに相当します。
c.f.:ラプラス変換のsは微分を表します。
Z変換の定義:
数列{uk}に対して、
![{\cal Z}[\{u_k\}]=\sum^{\infty}_{k=0}u_kz^{-k}=U(z)](eqn/digicont.bhtml.eqn103.gif)
と定義します。すなわち
数列→zの関数
になります。これによって、数列が代数式として扱えるようになります。
連続時間信号u(t)に対しても、サンプル値 u[k] をZ変換した物を u(t) のZ変換といいます。
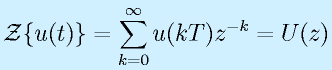
Z変換の性質
- 線形です。
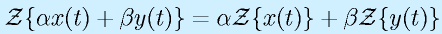
- zにより時間が進みます。
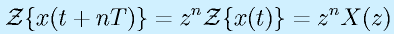
ここでnは整数、Tはサンプリング周期です。
Z逆変換
X(z)からx(kT)を復元する操作がZ逆変換です。
定義式は
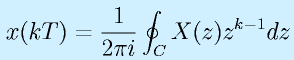
(Cは単位円)
ですが、手軽には、
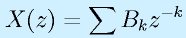
という形にできれば、x(kT)=Bk となります。
Z変換の例
- 単位ステップ:
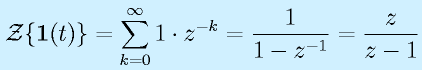
- 単位ランプ:
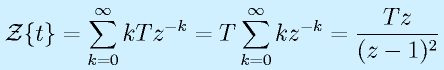
補足:
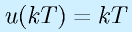
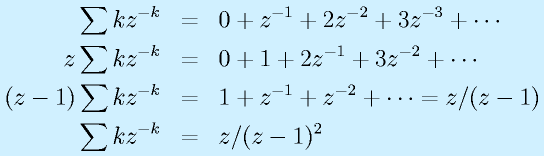
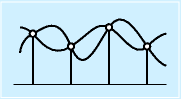
- インパルス列
x(t)は時刻t=kTのときのみ1,それ以外は0とします。
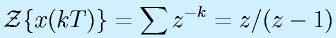
結果はステップと同じになります。別の見方をすれば、サンプルしてしまう場合は、サンプル間の部分は問えません。
逆に見ると、別の関数が同じZ変換になるということは、逆Z変換は一意にはもどせません。
離散時間線形系とパルス伝達関数
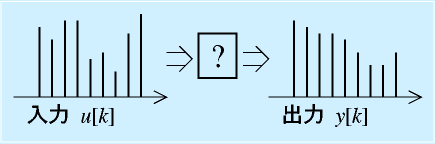
制御工学Iにおける伝達関数は、連続時間におけるシステムの入力と出力の関係をラプラス変換で表しました。
おなじように、離散時間における入出力関係を定係数差分方程式で表すことを考えます。
具体的には以下のような式で表します。
![&&y[k+n]+a_1y[k+n-1]+\cdots+a_ny[k]\nonumber\\&&~~~=b_0u[k+m]+b_1u[k+m-1]+\cdots+b_mu[k]](eqn/digicont.bhtml.eqn114.gif)
ここで、m,nは正の整数定数、y[i]は出力の系列を、u[i]は入力の系列を表します。u[k+m]とu[k]を比較すると、u[k+m]がより未来、u[k]がより過去の値となります。
この式を「n次定係数線形系」と呼びます(m次じゃないことに注意)。
これが実時間のシステムであるための条件は、
n≧m
です。なぜならば、m>nとすると、y[k+n]を決定するために、より未来の値 u[k+m]を必要とすることになるためで、その場合は実時間処理(データが流れてくる毎に即時処理すること)はできません。なお、演算に要する時間などを考慮すると、実際には「n>m」である必要があります。
(n=mだと、サンプリングタイミングが同じなら即時に結果を出さなければならない)
なお、一度録っておいたデータを後で処理する場合(オフライン処理)にはこの制約はありません。また、ラプラス変換の場合も、実現できるためには分母の次数のほうが高いという制約があります。
離散時間単位インパルス応答
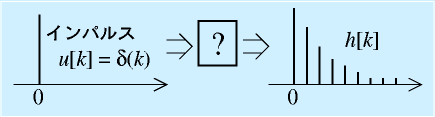 離散時間線形系に対して、入力 u[k]=δ(k)としたときの出力系列h[k]を(単位)インパルス応答といいます。
離散時間線形系に対して、入力 u[k]=δ(k)としたときの出力系列h[k]を(単位)インパルス応答といいます。
任意の入力 u[k] に対する出力は、この単位インパルス応答により
![y[k]=\sum_{l=0}h[l]u[k-l]](eqn/digicont.bhtml.eqn115.gif) :たたみ込み和
:たたみ込み和
によって得られます(ラプラス変換の場合はたたみ込み積分)。
例:
![u[k]=\{u_0,u_1,0,\cdots\}](eqn/digicont.bhtml.eqn116.gif)
としたき、y[1]は、一つ前であるu[0]に対する応答と、いまのu[1]に対する応答の和となるため、
![y[1]=u[0]h[1]+u[1]h[0]=\sum^{(1)}_{l=0}h[l]u[1-l]](eqn/digicont.bhtml.eqn117.gif)
となります。
パルス伝達関数
「出力のZ変換」/「入力のZ変換」をパルス伝達関数と呼びます。これは、単位インパルス応答h[l]があたります。
![y[k]=\sum_{l=0}h[l]u[k-l]](eqn/digicont.bhtml.eqn118.gif)
をZ変換すると、
![Y[z]=H(z)U(z),~~ H(z)=\sum h[z]z^{-k}](eqn/digicont.bhtml.eqn119.gif)
となります。
このパルス伝達関数は、差分方程式から直接求めることができます。
まず、差分方程式のZ変換をとります。
![&&y[k+n]\rightarrow z^nY(z), \cdots, y[k]\rightarrow Y(z) \nonumber\\&& u[k+m]\rightarrow z^mU(z), \cdots, u[k]\rightarrow U(z)](eqn/digicont.bhtml.eqn120.gif)
なので、
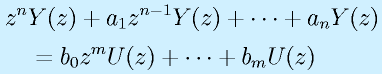
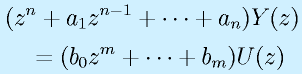
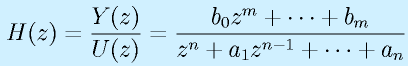
となります。このように差分方程式から直接的にパルス伝達関数を得ることができます。
繰り返しになりますが、実際にリアルタイム処理装置とする場合には、m≦nです(分子の次数が高い)。
ラプラス変換とZ変換
ラプラス変換のzが時間をT[s]進めるものであるため、ラプラス変換の exp(Ts)に相当するとして扱うことができます。つまり
![\sum h[k]z^{-k}&=&h[0]\delta(t)+h[1]\delta(t-T)+h[2]\delta(t-2T)+\cdots\nonumber\\&&\rightarrow h[0]+h[1]e^{-Ts}+h[2]e^{-2Ts}+\cdots](eqn/digicont.bhtml.eqn124.gif)
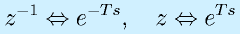
と置き換えることでZ変換のパルス伝達関数をラプラス変換の各種解析手法に持ち込むことができます。
また、
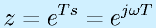
をパルス伝達関数に代入し、計算すれば、周波数ごとの伝達特性=ボード線図が得られます。
この逆変換を行うには、
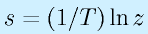
が正確ですが、実際には式として扱いにくいという問題があります。そこで、
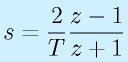 双一次変換
双一次変換
で代用します。この双一次変換は、安定性の確認などでも互換性をもつ、似た特性をもっています。
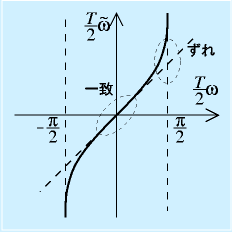
参考:双一次変換の特性:
双一次変換の周波数特性は
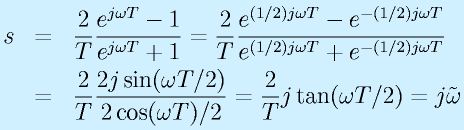
で与えれる。ここで〜ωは本来のはs=jwであることから比較のために導入しています。
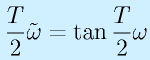
という関係になりますが、ωが0に近いうちは、ωと〜ωはほぼ一致し、Tω/2がπ/2に近づくと、ずれが大きくなっていきます。これは
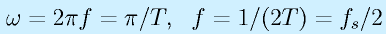
で、サンプリング周波数の半分、つまりサンプリング定理に抵触するあたりです。
パルス伝達関数の実体化
 設計したパルス伝達関数を実装するには、遅延素子を用います。
遅延素子は、たとえば、ソフトウエアで実装する場合はメモリ上の変数、ハードウェアで実装する場合は、D-FFなどを用います。
設計したパルス伝達関数を実装するには、遅延素子を用います。
遅延素子は、たとえば、ソフトウエアで実装する場合はメモリ上の変数、ハードウェアで実装する場合は、D-FFなどを用います。
右図はパルス伝達関数を実装するためのブロック図です。[D]はサンプリング周期1回分/系列1個分の遅延素子で、Z^{-1}に相当します。
入力u[k]および出力y[k]を遅延させ、パルス伝達関数から求めた差分方程式をもとに出力y[k]を求めます。
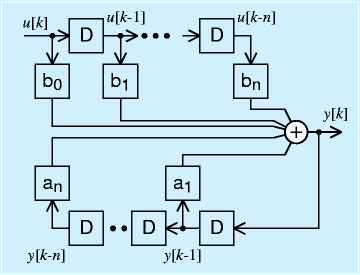
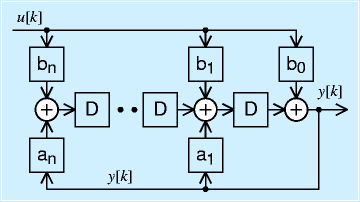 右図はパルス伝達関数の実装方法の別手法です。
右図はパルス伝達関数の実装方法の別手法です。
先ほどと大きく形が変っていますが、良く見ると、たとえば、any[k-n]の項は、最初にy[k]にanを乗じたの値、n個のDを経て最後にたどり着きます。つまり、遅延してから係数を乗じるのではなく、係数を乗じ、他の項といっしょに必要なだけ遅延するようになっています。
この実装は、見てわかるようにDが約半分ですみます(加算の回数は増える)。そのためメモリを削減するなどにいいのですが、これをそのまま実装すると、後でみて内容が分かりにくくなるという点が問題と言えます(=一度作ったら終りなシステムには問題ない)。
ディジタルフィルタ
上で述べたように、パルス伝達関数を実装することで、各種伝達関数をコンピュータ上で実装することができます。
しかし、なんらかの制御系をラプラス変換の伝達関数の上で設計して、わざわざパルス伝達関数に直してから実装するということは少なく、普通は最初のPID制御で済ませてしまうのが実情です。
しかし、取り込んだ信号を様々に処理するという点では、「ディジタルフィルタ」として非常によく使われます。ここでは、ディジタルフィルタとしての応用を主眼に、簡単に見ていきます。
FIRフィルタ
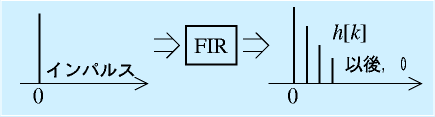 ディジタルフィルタで主流なものは FIR(Finite Impulse Respose)フィルタです。
名前の通り、パルス伝達関数はFinite、すなわち有限のインパルス応答を持つフィルタです。
ディジタルフィルタで主流なものは FIR(Finite Impulse Respose)フィルタです。
名前の通り、パルス伝達関数はFinite、すなわち有限のインパルス応答を持つフィルタです。
FIRの例:
![h[0]=h[1]=\frac{1}{2},~~~H(z)=\frac{1}{2}+\frac{1}{2}z^{-1}](eqn/digicont.bhtml.eqn151.gif)
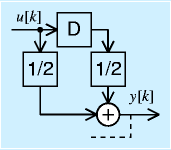 このパルス伝達関数を差分式に戻すと、
このパルス伝達関数を差分式に戻すと、
![y[k]=\frac{1}{2}(u[k]+u[k-1])](eqn/digicont.bhtml.eqn152.gif)
となり、よく知られた移動平均フィルタになります。
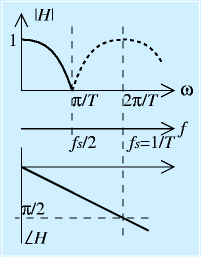 この特性を求めてみます。
この特性を求めてみます。
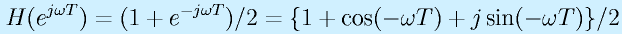
ここで、
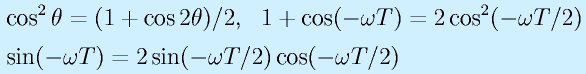
を利用して書き換えると、
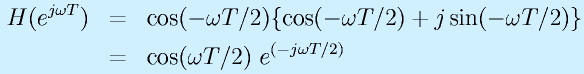
となります。よって、この伝達関数のゲインと位相は
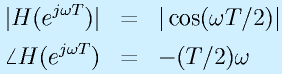
となります。これは、ゲインは ωT/2=π/2、すなわち、2πf=π/T=πfs, f=fs/2のとき、つまりサンプリング周波数の1/2の周波数に対してゲインがゼロ、十分周波数がひくいとゲインが1といった特性になり、かつ、位相遅れはωに比例します(サンプリング周波数の半分でπ/2遅れる)。
FIRフィルタはその特徴として、位相遅れが直線的になり、その傾きは次数に比例します。
さらに、別の見方をすると、時間遅れが周波数に依存しません(上の例だと、T/2が遅れになる)。
そのため、
- 波形を入れたときに周波数毎に遅延のずれが生じないため、波形が大きく崩れない。
- フィードバックループにいれると、周波数が高いところで大きな遅延を生じて発振する可能性が高い。
という特徴を持ちます。そのため、ループに入れなかったり遅延が気になりにくい処理、たとえば音の信号の処理や、オフラインでの信号処理に向いた方式です。
また、フィルタ特性の数学的な設計手法が様々に提案されています。
IIRフィルタ
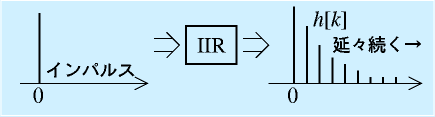 ディジタルフィルタにはもう一つ、IIR(Infinite Impulse Response)型のフィルタがあります。
名前の通り、パルス伝達関数はInfinite、すなわち無限の長さを持ちます。
ディジタルフィルタにはもう一つ、IIR(Infinite Impulse Response)型のフィルタがあります。
名前の通り、パルス伝達関数はInfinite、すなわち無限の長さを持ちます。
IIRの例:
![y[k]=ru[k]+(1-r)y[k-1]](eqn/digicont.bhtml.eqn157.gif)
これは、手軽に使えるローパスフィルタの一種です。パラメータはrのみで、入力を比率rだけ徐々に混ぜ込んでいくような特性を持っています。r=1のときは、見ての通りただの素通し、r=0のときは、y[k]=y[k-1]、すなわち値を維持します。
これをZ変換すると、
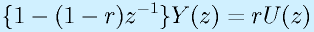
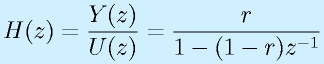
となります。
たとえば、r=1/2のとき、
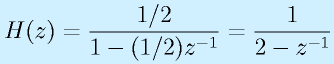
となります。おおざっぱに特性を見ると、
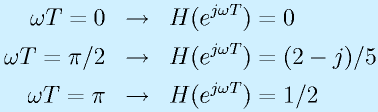
(f=0, f=(1/4)fs, f=(1/2)fs, @(1/4)fs |H|=0.45, くH=-26.6deg)
となっています。
実用時には、ふつうは、このrを0.01など、小さな値にします。
IIRの例2:
つぎに、アナログフィルタの伝達関数をもとに、双一次変換を用いて、パルス伝達関数にもっていってみます。
アナログ伝達関数:
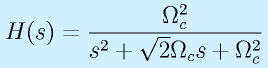
2次バタワース特性ローパスフィルタ、カットオフΩc、40dB/dec
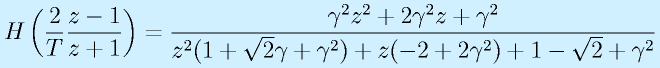
ただし、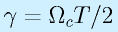 とおいています。
とおいています。
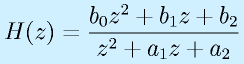
ただし、
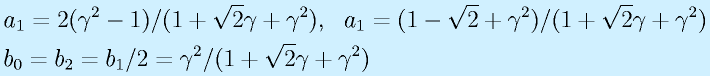
です。
これを、
![y[k]=-a_1y[k-1]-a_2y[k-2]+b_0u[k]+b_1u[k-1]+b_2[k-2]](eqn/digicont.bhtml.eqn167.gif)
という式で実装すれば、ほぼ、目的の特性が得られます。
ここで注意すべき点は、この特性は、サンプリング周期(周波数)によって無次元化されたγで表されていることです。
ひとたび、双一次変換して得たパルス伝達関数のカットオフ周波数は、サンプリング周波数に依存します。
つまり、サンプリング周波数を2倍にすると、カットオフも2倍になります。
これが便利なこともありますが、うっかりを招くこともあるので、離散系では常にサンプリング周波数の変更はなにかを引き起こすと心得ておくべきでしょう。
もう一点、演算精度にも注意が必要なことがあります。
通常は、アナログフィルタに比べて、ディジタルフィルタのほうが有効桁数が確保しやすいのですが、今回のフィルタを例にすると、γが極端に小さい場合、つまり、サンプリング周波数に対してカットオフがかな低い場合、係数a,bの比を見ると、共通の分母を払った状態で、a1,a2はほぼ1程度のオーダーなのに対してb0,b1,b2はγ2乗のオーダーです。たとえばγが0.001だとすると、有効桁数が7桁の単精度実数(float)では精度が足りなくなります。気づかないうちに謎の答えが出るのが桁落ちの恐怖なので、これも心に留めておくと良いでしょう。
まとめ
このページでは、今日、制御などを行う上で避けて通ることのできない、コンピュータによるディジタル制御、ディジタル信号処理にまつわる基本事項についてまとめました。
制御をするにいたらなくとも、実験結果の処理などで信号処理を扱うことは多いと言え、その場合にも、サンプリングの問題、ディジタル化するための量子化の問題があり、適切なフィルタ処理など、なんらかの役に立つことと思います。
熊谷正朗
[→連絡]
東北学院大学
工学部
機械知能工学科
RDE
[| ]
 右図にコンピュータ制御システムの構成例を示します。
右図にコンピュータ制御システムの構成例を示します。 コンピュータに値を取り込む際には、AD変換器が用いられます。
これは入力電圧をたとえば0〜255などの整数に置き換える回路です。
コンピュータに値を取り込む際には、AD変換器が用いられます。
これは入力電圧をたとえば0〜255などの整数に置き換える回路です。 本来、電気信号は時間的にも連続です。しかし、AD変換器は変換するのに多少の時間がかかります。また、それをコンピュータで処理して出力する場合もかならず時間を要します。
本来、電気信号は時間的にも連続です。しかし、AD変換器は変換するのに多少の時間がかかります。また、それをコンピュータで処理して出力する場合もかならず時間を要します。 上でも触れたように、AD変換を行う際には、入力のある範囲は一つの値にまとめられ、結果的にADの入力と変換値の関係は階段状になります。これは期待される直線的な対応とはノコギリ状の誤差が発生します。
上でも触れたように、AD変換を行う際には、入力のある範囲は一つの値にまとめられ、結果的にADの入力と変換値の関係は階段状になります。これは期待される直線的な対応とはノコギリ状の誤差が発生します。 サンプリングに伴う、もっとも有名な問題がサンプリング定理と呼ばれる、信号の変化とサンプリング時間間隔の関係に由来する問題です。
サンプリングに伴う、もっとも有名な問題がサンプリング定理と呼ばれる、信号の変化とサンプリング時間間隔の関係に由来する問題です。 サンプリングに関連して、もう一つの現象があります。
サンプリングしているところに、1/2を越える信号を入れてしまうとどうなるか、という問題です。
サンプリングに関連して、もう一つの現象があります。
サンプリングしているところに、1/2を越える信号を入れてしまうとどうなるか、という問題です。 一方、出力側にも同じような問題があります。
一方、出力側にも同じような問題があります。 これらの問題に対応するため、一般に、AD、DA変換の前後には、アナログ回路のローパスフィルタ(低い周波数のみを通すフィルタ)をいれます。これにより、
これらの問題に対応するため、一般に、AD、DA変換の前後には、アナログ回路のローパスフィルタ(低い周波数のみを通すフィルタ)をいれます。これにより、
 そもそも、積分の概念は、右図のように、なんらかの関数があったときに、それがゼロと囲む範囲の面積をもとめるように、短冊状に切り、各々の短冊の面積を積算していく計算です。
本来の積分では、短冊の幅を極限まで小さくすることで、短冊の端と対象関数の形状の差を限りなくゼロに近づけています。
そもそも、積分の概念は、右図のように、なんらかの関数があったときに、それがゼロと囲む範囲の面積をもとめるように、短冊状に切り、各々の短冊の面積を積算していく計算です。
本来の積分では、短冊の幅を極限まで小さくすることで、短冊の端と対象関数の形状の差を限りなくゼロに近づけています。 本来の微分は、ある時点での関数の変化率を求めます。定義では、狭い時間間隔の2点での関数値を求め、その傾きを出し、その上で、時間間隔を極限まで狭めます。(図(1))
本来の微分は、ある時点での関数の変化率を求めます。定義では、狭い時間間隔の2点での関数値を求め、その傾きを出し、その上で、時間間隔を極限まで狭めます。(図(1))
 制御工学Iにおける伝達関数は、連続時間におけるシステムの入力と出力の関係をラプラス変換で表しました。
制御工学Iにおける伝達関数は、連続時間におけるシステムの入力と出力の関係をラプラス変換で表しました。 離散時間線形系に対して、入力 u[k]=δ(k)としたときの出力系列h[k]を(単位)インパルス応答といいます。
離散時間線形系に対して、入力 u[k]=δ(k)としたときの出力系列h[k]を(単位)インパルス応答といいます。 参考:双一次変換の特性:
参考:双一次変換の特性: 設計したパルス伝達関数を実装するには、遅延素子を用います。
遅延素子は、たとえば、ソフトウエアで実装する場合はメモリ上の変数、ハードウェアで実装する場合は、D-FFなどを用います。
設計したパルス伝達関数を実装するには、遅延素子を用います。
遅延素子は、たとえば、ソフトウエアで実装する場合はメモリ上の変数、ハードウェアで実装する場合は、D-FFなどを用います。 右図はパルス伝達関数の実装方法の別手法です。
右図はパルス伝達関数の実装方法の別手法です。 ディジタルフィルタで主流なものは FIR(Finite Impulse Respose)フィルタです。
名前の通り、パルス伝達関数はFinite、すなわち有限のインパルス応答を持つフィルタです。
ディジタルフィルタで主流なものは FIR(Finite Impulse Respose)フィルタです。
名前の通り、パルス伝達関数はFinite、すなわち有限のインパルス応答を持つフィルタです。 このパルス伝達関数を差分式に戻すと、
このパルス伝達関数を差分式に戻すと、 この特性を求めてみます。
この特性を求めてみます。 ディジタルフィルタにはもう一つ、IIR(Infinite Impulse Response)型のフィルタがあります。
名前の通り、パルス伝達関数はInfinite、すなわち無限の長さを持ちます。
ディジタルフィルタにはもう一つ、IIR(Infinite Impulse Response)型のフィルタがあります。
名前の通り、パルス伝達関数はInfinite、すなわち無限の長さを持ちます。