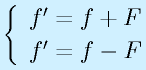ここでは非線型な対象を扱う方法を考えます。
古典制御、これまで扱った現代制御理論とも、対象は線形です。線形というのはたとえば
- f(a+b)=f(a)+f(b)
- f(ca)=cf(a) (cは定数)
などの性質を持つ物です。単純な対象は線形なことも多いのですが、実際に制御対象にしたいものは非線形なことが一般的です。
運動方程式に三角関数が入ったらそれでもう非線形なので、たとえば、回転関節をもつロボットなどは非線形な対象の例です。
非線形がからむ制御としては、
- 制御対象が非線形
- 連続な非線形の式で表される(リンク機構、重力など)
- 不連続な式で表される(摩擦など)
- 制御手法が非線形
- 連続非線型な制御則(ニューラルネットなども含む)
- 不連続な制御(ON/OFF制御<こたつなど)
などに分類できます。
これらに対する一般的な対処法としては、
- 線形化:
非線型なものも、部分的に見れば線形に近似できる。
- 記述関数法:
対象となるシステムに正弦波を入れ、その出力から擬似的に伝達関数化して解析、制御。
- 位相面解析:
2次系(x, dx/dt, d2x/dt2)のシステムで、(x, dx/dt)の挙動をグラフ上で解析。
- 非線形には非線形で:
非線型な要素を、非線型な入力でキャンセルして、線形にするor線形に近づける。
などがあります。
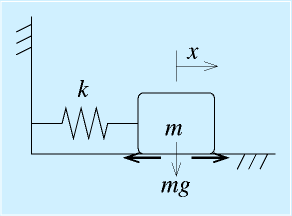
実際にものを作ると対処しなければならないややこしいものに、摩擦があります。
たとえば、右図のようなバネマス系の場合、摩擦がなければ、
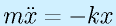
と単純な式になりますが、動摩擦があるとすると、
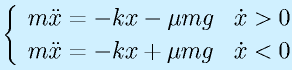
というように、運動方向に応じて摩擦力のかかり方はかわります。
また、止まった場合には静止摩擦も考慮する必要があります。
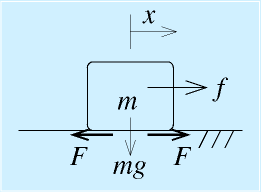 右図に示すような、摩擦があるところの物体の制御の仕方を検討します。
右図に示すような、摩擦があるところの物体の制御の仕方を検討します。
運動方程式は
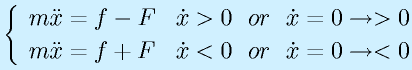
となります。ここで、fは物体の運動のために作用させる力、Fは摩擦力です。
後ろの条件で、前者は運動中、後者は静止から運動開始、つまり止まっているものを動かそうという静摩擦への対応です。ちなみに、止まっている場合には、上式でf-F≧0、下式でf+F≦0です(摩擦力で走り出すことはない)。
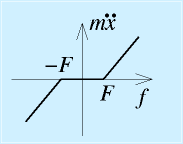 おおざっぱに図示すると、右図のようになります。力をかけても加速せず、ある程度力をかけると、摩擦力を振り切るのに十分になって加速を開始する、という感じです。このように、操作しても結果が出ない部分を不感帯といいます。
おおざっぱに図示すると、右図のようになります。力をかけても加速せず、ある程度力をかけると、摩擦力を振り切るのに十分になって加速を開始する、という感じです。このように、操作しても結果が出ない部分を不感帯といいます。
この対象の制御を考えます。
(1)PID制御
積分項によって、目標に達する前に停止すると、誤差積分値が蓄積するため、いつかは静止摩擦力を振り切って動き出します。
しかし、一般に静止摩擦力よりも動摩擦力が小さいため、一旦動き出すと、目標を通りすぎてからP制御によって停止し、また同じことを繰り返します。そのため、なかなか目標地点に到達しません。
(2)摩擦補償
運動状況をもとに、
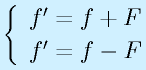
を操作量とします。つまり、摩擦で目減りする分をあらかじめ加えておきます。
理論的に正確に摩擦をモデル化することは困難ですが、実際にシステムを組んだ状態で測定した値を加えてやるだけでも、動作は劇的に改善する場合があります。
※測定法:PI制御にしておいて動き出す瞬間の操作量を測定する、手動で操作量を調整して動き出すところを調べる、など
摩擦補償は、重力補償に比べるとぴたりとはまることはあまりありません。
ただ、重力の場合にはあくまで連続的なのに対して、摩擦は不連続でもあるため、経験上、いやなトラブルが多くありました。
そのときに、おおざっぱに上式のような補償を加えてやると、それだけで改善が見られました。
世の中は線形なものより非線型なもののほうが多いと言えます。
すべてに対処することは無理で、線形化や補償を考えるためのモデル化も困難な場合がよくあります。
ただ、おおざっぱでもここで説明したような細工をすると、改善することが多いため、アイデアとして覚えておくといいと思います。
このページ、ここで終了。
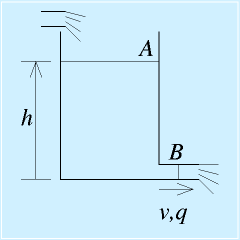 右の図に示すような、タンクの液面の高さの制御をすることを考えます。
右の図に示すような、タンクの液面の高さの制御をすることを考えます。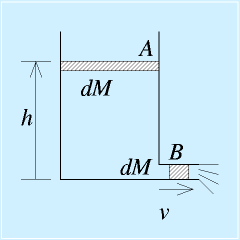 まず、対象の方程式を立てます。
まず、対象の方程式を立てます。![]()
![]()
![]()
![]()
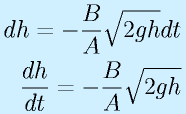
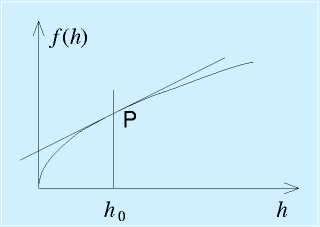 これをある高さh0近辺で液面を一定に保つような制御を行う場合、その近辺に限ってみれば、あまり極端な変化はありません。
そこで、h0近辺で1次式で近似してみます。
これをある高さh0近辺で液面を一定に保つような制御を行う場合、その近辺に限ってみれば、あまり極端な変化はありません。
そこで、h0近辺で1次式で近似してみます。![]()
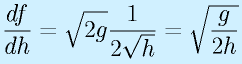
![]()
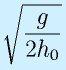
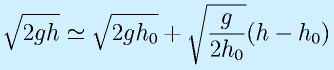
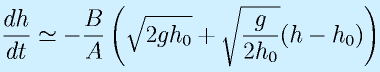
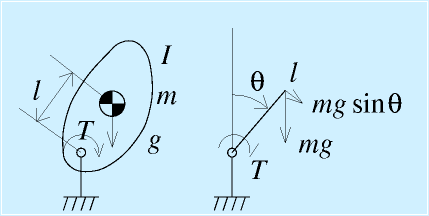 右図に示すような、ごく単純なアーム状のものを考えます。
根本を回転ジョイントで支えられ、鉛直面内で傾きを制御するような対象です。
右図に示すような、ごく単純なアーム状のものを考えます。
根本を回転ジョイントで支えられ、鉛直面内で傾きを制御するような対象です。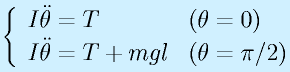
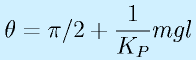
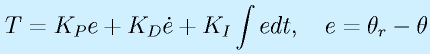 (θr:目標角度)
(θr:目標角度)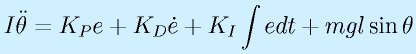
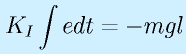
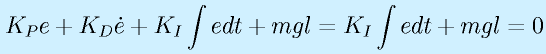
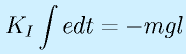
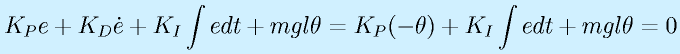
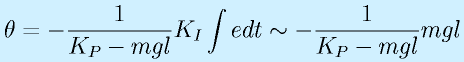
 実際にものを作ると対処しなければならないややこしいものに、摩擦があります。
実際にものを作ると対処しなければならないややこしいものに、摩擦があります。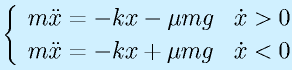
 右図に示すような、摩擦があるところの物体の制御の仕方を検討します。
右図に示すような、摩擦があるところの物体の制御の仕方を検討します。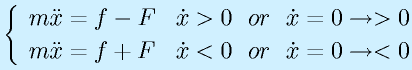
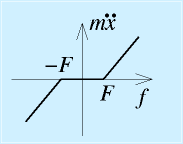 おおざっぱに図示すると、右図のようになります。力をかけても加速せず、ある程度力をかけると、摩擦力を振り切るのに十分になって加速を開始する、という感じです。このように、操作しても結果が出ない部分を不感帯といいます。
おおざっぱに図示すると、右図のようになります。力をかけても加速せず、ある程度力をかけると、摩擦力を振り切るのに十分になって加速を開始する、という感じです。このように、操作しても結果が出ない部分を不感帯といいます。