例:
温度を入力とする「暖かい」という集合のメンバシップ関数:
たとえば
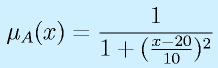
などと設定。x=20のとき、μA=1.0、x=10(ちと寒い?)、30(暖かいと言うより暑い)のとき、μA=0.5などと分布ができます。
ものを制御する際、制御工学Iやこれまで扱ってきたような「きっちり数式で表して、きっちり理論をチェックして、きっちり制御する」方法ですまないことは良くあります。最近ではコンピュータの能力も上がってきたので、モデル化がきっちりできれば現代制御理論で大規模に制御もかけられますが、そもそもモデル化できないときに困ります。
モデル化できない物でもある程度性格が単調なら、PID制御のような汎用の方法で制御できますが、そうも行かない物がよくあります。
ところが、機械仕掛けで数式で制御する方策が見あたらなくとも、熟練した人間が操作すれば一発、ということもあります。
また、人間をはじめ、生物は神経系に学習することで、さまざまな行動をとることができます。
制御のパラメータがなかなか見つからなくとも、数打ちゃ当たることもあります。
そういった、これまでの数式理論ベースではない、いまどき使われている制御の概要を見てみることにします。
ファジー制御は人間の「こういうときはこうする」という経験則を制御などに活かしやすくした手法です。 一時期、家電で「ファジィ」「ニューロファジィ」というのが流行りましたが(いまもストーブなどについていますが)、それです。 また、仙台市の地下鉄の車両運転制御システムはその代表的な応用例として有名?です。
人間がなにかするとき、それまでの経験などから「こういうときはこうする」「ああいうときはああする」のように、状況に対してとるべき行動を持って調整します。ディジタルな場合にはそれぞれ0か1かしかありませんが、実際には「このくらいならこのくらいで」のように「程度」も含めて、多くのルールを持った上で、動作を決めます。
対象をモデル化することなく、制御の数式に載せることなく、人間の持つこうした経験、知識のルールを集めて行う制御です。
まず、現象をファジィ化します。集合(条件)への合致具合をメンバシップ関数と呼ばれる関数で表します。
例:
温度を入力とする「暖かい」という集合のメンバシップ関数:
たとえば
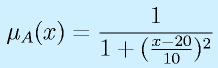
などと設定。x=20のとき、μA=1.0、x=10(ちと寒い?)、30(暖かいと言うより暑い)のとき、μA=0.5などと分布ができます。
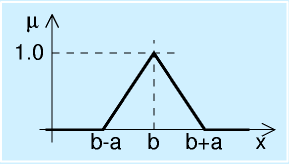 実用上は、より計算を簡単にするために、三角型がよく用いられます。
実用上は、より計算を簡単にするために、三角型がよく用いられます。
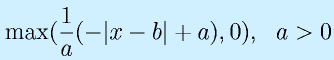
(x=bで1.0、b±aで0.0になるような三角型)
ファジィ制御系は制御対象の状態量をファジィ化し、制御の方法をまとめたファジィルールによってファジィ推論を行い、その結果を脱ファジィ化という操作によって操作量にして対象に入力します。以下では、その簡単な例を見てみます。
例:冷房装置
ルール1:寒い(A1)なら、出力を小さくする(B1)
ルール2:快適(A2)なら、出力を中ぐらいにする(B2)
ルール3:暑い(A3)なら、出力を大きくする(B3)
演算方法:
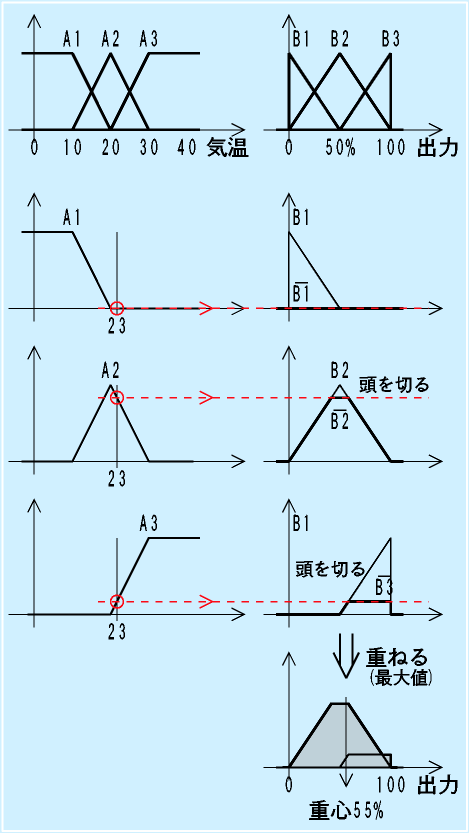
上図のメンバシップ関数に従って、まず、温度から集合Aへの適合度を求めます。
次に、ルールで対応づけられた関数Bにおいて、適合度で山の頭を切ります。
頭を切ったBの関数を重ね合わせ、最大値をとります。
最後にその重心をとって、操作量を決定します。
例:23度の場合
利点:
生物の神経回路網を模擬した信号の処理手法です。
ある入力を与えたときに、こういう出力が欲しい、という用途に、神経回路網を模擬した物をつかいます。
生物は各種感覚器などの信号を神経細胞に集め、その細胞毎に次の出力がでます。これがまた別の神経細胞に入力されます。
その際、信号がどの程度細胞の出力に寄与するかが、シナプスと呼ばれるところの結合度合で定まり、結果的に各入力の結合度合の組み合わせでその細胞の出力がきまります。また、結合度合は何らかの形で徐々に修正されていきます。これが学習です。
ニューラルネットワークでは、神経細胞とその結合を模した手法を用い、さらに入力と出力のペアを多数与えることで学習もさせます。
あるパターンに対する出力を出す、という機能をもつため、パターン認識などにも用いられる他、学習させた数値と数値の間の入力に対する出力を得るような補間に用いたり、実在のシステムの入出力を与えることで、未知のシステムのモデル化などに使用できます。
ニューラルネットは神経細胞ニューロンとその接続方法の大きく二つの設定箇所があります。
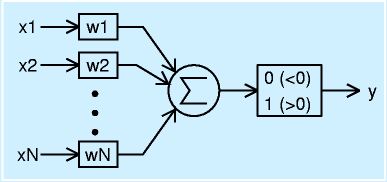 単一のニューロンは多入力1出力の関数として表され、たとえば、
単一のニューロンは多入力1出力の関数として表され、たとえば、
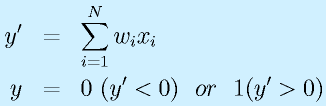
のような関数を用います。ここでxiはi番目の入力、wiはその入力に対する重みです。
ここでは、単純な二値化の出力を例示しましたが、その定義で様々な特性を持たせることができます。
このニューロンに対する学習は、入力信号と出力のセットである学習データを多数与えることで繰り返し行います。
ニューロンの関数を、
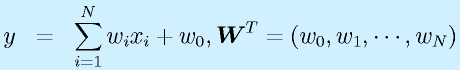
とした場合、学習データ
![\vect{X}[k]=\Mqo{1}{x_1[k]}{\vdots}{x_N[k]}, d[k]](eqn/othercontrol.bhtml.eqn153.gif)
を与えて、たとえば、
![e[k]&=&d[k]-\vect{W}^T\vect{X}[k]\nonumber\\ \vect{W}[k+1]&=&\vect{W}[k]+2\mu \vect{X}[k]e[k]](eqn/othercontrol.bhtml.eqn154.gif)
と、重みベクトルWを修正していきます(eは誤差)。μはどのくらい修正するかを決める学習係数で大きくすると学習は早く進みますが、修正しすぎて発散することもあります。多くのデータを繰り返し与え、学習させることで重みが適当に設定されます。
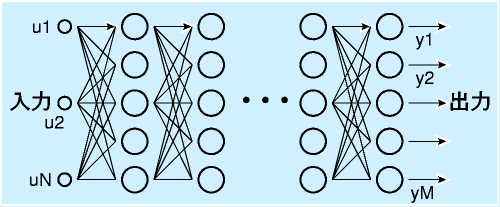 このニューロンを複数の層状に接続して、多層ニューラルネットワークを構成します。
入力に直結した入力層、出力に直結した出力層と、間に一つ以上の中間層をはさみます。
これだけ複雑になると学習のさせかたがぴんと来ませんが、誤差逆伝播法(back propagation method)などの手法が提案されています。
このニューロンを複数の層状に接続して、多層ニューラルネットワークを構成します。
入力に直結した入力層、出力に直結した出力層と、間に一つ以上の中間層をはさみます。
これだけ複雑になると学習のさせかたがぴんと来ませんが、誤差逆伝播法(back propagation method)などの手法が提案されています。
利点:
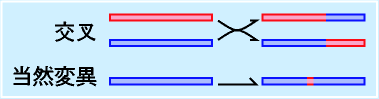
遺伝的アルゴリズム(Genetic Algorithm, GA)は、制御パラメータの決定などを行うために、進化論的な考え方を応用した手法です。
生物の進化では
利点: