プチテスト・レポート2004

最終更新： 2011/02/10 19:32:08 ［｜　］　最終更新： 2011/02/10 19:32:08

このページは

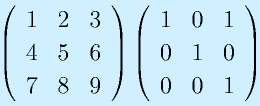
このページは講義に関連して実施した、プチテスト、レポートの解答例です。講義で解けなかったときや、あとでやりかたを忘れてしまったときなどに見てください。なお、解答作成には万全の注意を払っていますが、間違いを見つけた場合には至急連絡をお願いします。

プチテスト

9/14　ぷち０：力試し

Ｑ１：
下記の行列の積をもとめよ
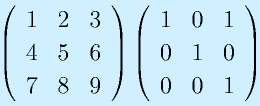
$\Mss123456789 \Mss101010001$

Ｑ２：
下記の行列の固有値を求めよ
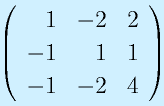
$\Mss1{-2}2{-1}11{-1}{-2}4$

Ａ１：
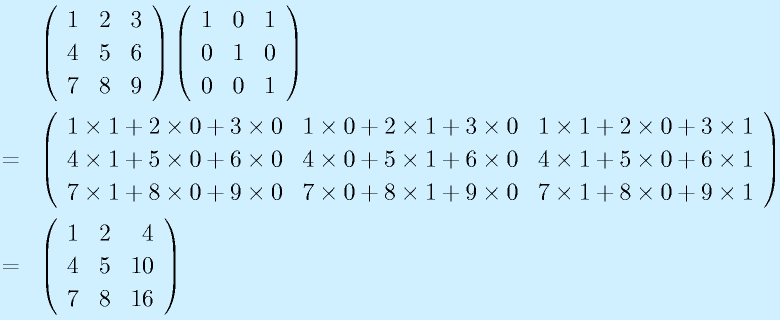
$&&\Mss123456789 \Mss101010001\nonumber\\&=&\Mss{1\times1+2\times0+3\times0}{1\times0+2\times1+3\times0}{1\times1+2\times0+3\times1}{4\times1+5\times0+6\times0}{4\times0+5\times1+6\times0}{4\times1+5\times0+6\times1}{7\times1+8\times0+9\times0}{7\times0+8\times1+9\times0}{7\times1+8\times0+9\times1}\nonumber\\&=&\Mss12445{10}78{16}$

Ａ２：
つかう数学：計算例の一番下で解説すみ。

9/28　ぷち１：逆行列

Ｑ１：
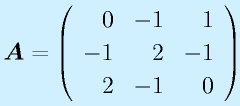
$\vect{A}=\Mss{0}{-1}{1}{-1}{2}{-1}{2}{-1}{0}$
の逆行列を求めよ。
Ｑ２：
求めた逆行列ともとの行列の積が単位行列になることを確認せよ。

Ａ１：
まず、逆行列を持つことを確認する意味でも、行列式を求める。
$|\vect{A}|=0+2+1-(4+0+0)=-1$
０ではないので、逆行列をもつ。

次に余因子行列を求める
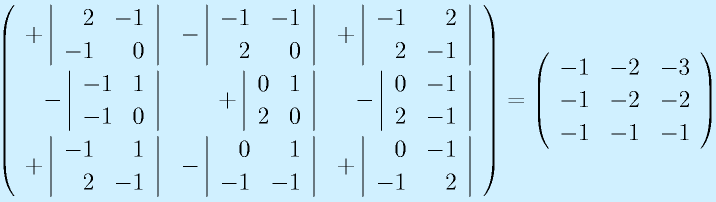
$\Mss{+\left|\begin{array}{rr}2&-1\\-1&0\end{array}\right|}{-\left|\begin{array}{rr}-1&-1\\2&0\end{array}\right|}{+\left|\begin{array}{rr}-1&2\\2&-1\end{array}\right|}{-\left|\begin{array}{rr}-1&1\\-1&0\end{array}\right|}{+\left|\begin{array}{rr}0&1\\2&0\end{array}\right|}{-\left|\begin{array}{rr}0&-1\\2&-1\end{array}\right|}{+\left|\begin{array}{rr}-1&1\\2&-1\end{array}\right|}{-\left|\begin{array}{rr}0&1\\-1&-1\end{array}\right|}{+\left|\begin{array}{rr}0&-1\\-1&2\end{array}\right|}=\Mss{-1}{-2}{-3}{-1}{-2}{-2}{-1}{-1}{-1}$
逆行列はこれを転置して、かつ、行列式で割って得られるので、
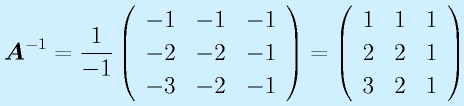
$\vect{A}^{-1}=\frac{1}{-1}\Mss{-1}{-1}{-1}{-2}{-2}{-1}{-3}{-2}{-1}=\Mss111221321$
となる。
※解答の中で、上式の中間で止まっている例が大半を占めましたが、常識の範囲で負号を全部相殺すべきです。そうでなくとも、負号を行列の中にいれること。

Ａ２：
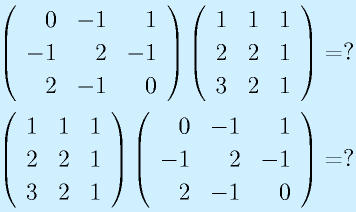
$\Mss{0}{-1}{1}{-1}{2}{-1}{2}{-1}{0}\Mss111221321 = ?\nonumber\\\Mss111221321\Mss{0}{-1}{1}{-1}{2}{-1}{2}{-1}{0} = ?$
ちゃんと計算みること。"=I"と書くだけなら簡単ですが、なんのチェックにもなりません。

10/12　ぷち２：固有値固有ベクトル

Ｑ：
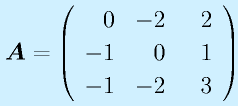
$\vect{A}=\Mss{0}{-2}{2}{-1}{0}{1}{-1}{-2}{~~3}$
の固有値と対応する固有ベクトルを求めよ。

まず、固有値を求める。
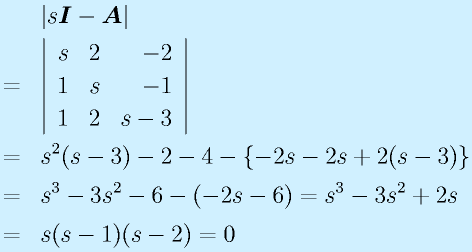
$&&|s\vect{I}-\vect{A}|\nonumber\\ &=&\left|\begin{array}{rrr}s&2&-2\\1&s&-1\\1&2&s-3\end{array}\right|\nonumber\\ &=& s^2(s-3)-2-4-\{-2s-2s+2(s-3)\} \nonumber\\&=&s^3-3s^2-6-(-2s-6)=s^3-3s^2+2s\nonumber\\&=&s(s-1)(s-2)=0$
よって、固有値は0,1,2である。

次に、個々の固有値に対応する固有ベクトルを求める。
$(s\vect{I}-\vect{A})\vect{v}=\vect{0}$
s1=0:
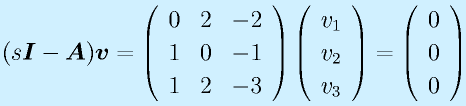
$(s\vect{I}-\vect{A})\vect{v}=\Mss{0}{2}{-2}{1}{0}{-1}{1}{2}{-3}\Mso{v_1}{v_2}{v_3}=\Mso000$
よって、
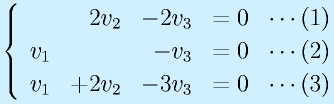
$\left\{\begin{array}{rrrr} & 2v_2 & -2v_3 &=0~~\cdots(1)\\ v_1 & & -v_3 &=0~~\cdots(2)\\ v_1& +2v_2 & -3v_3 &=0~~\cdots(3)\end{array}\right.$
となる。(1)および(2)より、v2=v3, v1=v3 という関係が得られるため、たとえば、v3=1とおくと、s1=0に対応する固有ベクトル、
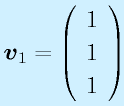
$\vect{v}_1=\Mso111$
を得ることができる。((3)式は(1),(2)の組で表される)
なお、
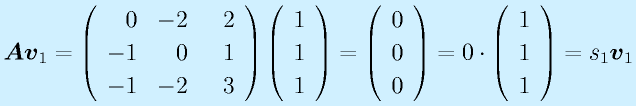
$\vect{Av}_1=\Mss{0}{-2}{2}{-1}{0}{1}{-1}{-2}{~~3}\Mso111=\Mso000=0\cdot\Mso111=s_1\vect{v}_1$
であり、固有値、固有ベクトルの関係式
$\vect{Av}_i=s_1\vect{v}_i$
を満たすことが確認される。
※v1=v2=v3=0とすると、そもそもの固有ベクトルの定義に反する。

s2=1:
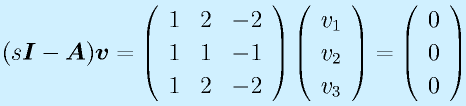
$(s\vect{I}-\vect{A})\vect{v}=\Mss{1}{2}{-2}{1}{1}{-1}{1}{2}{-2}\Mso{v_1}{v_2}{v_3}=\Mso000$
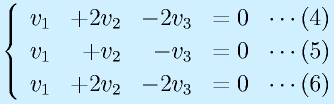
$\left\{\begin{array}{rrrr} v_1& +2v_2 & -2v_3 &=0~~\cdots(4)\\ v_1 & +v_2 & -v_3 &=0~~\cdots(5)\\ v_1& +2v_2 & -2v_3 &=0~~\cdots(6)\end{array}\right.$
ここで、(5)式を２倍し、そこから(4)式を引くと、v1=0が決定する。
あとは、残りの式はすべて v2=v3となるので、v2=1とすると、
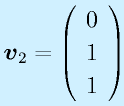
$\vect{v}_2=\Mso011$
を得ることができる。Av=svの関係は各自確認すること。
※固有ベクトルはすべての要素が０になるものが不可であって、一つの要素が０といった場合は問題ありません。。

s2=2:
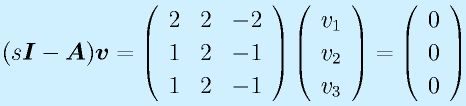
$(s\vect{I}-\vect{A})\vect{v}=\Mss{2}{2}{-2}{1}{2}{-1}{1}{2}{-1}\Mso{v_1}{v_2}{v_3}=\Mso000$
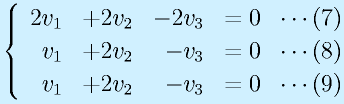
$\left\{\begin{array}{rrrr} 2v_1& +2v_2 & -2v_3 &=0~~\cdots(7)\\ v_1 & +2v_2 & -v_3 &=0~~\cdots(8)\\ v_1& +2v_2 & -v_3 &=0~~\cdots(9)\end{array}\right.$
ここで、(8)式から、(7)を(1/2)したものを引くと、v2=0が決定する。あとは、残りの式はすべて v1=v3となるので、v1=1とすると、
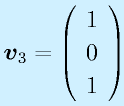
$\vect{v}_3=\Mso101$
を得ることができる。
なお、
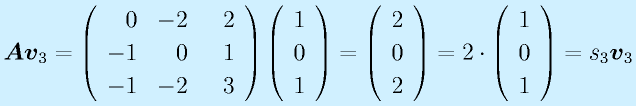
$\vect{Av}_3=\Mss{0}{-2}{2}{-1}{0}{1}{-1}{-2}{~~3}\Mso101=\Mso202=2\cdot\Mso101=s_3\vect{v}_3$
であり、固有値、固有ベクトルの関係式
$\vect{Av}_i=s_1\vect{v}_i$
を満たすことが確認される。

レポート

11/2 状態方程式、可制御、可観測

モータを制御対象として、状態方程式を立て、可制御性、可観測性についてしらべます。
→詳細(PDF)

注意：講義で配布した専用用紙のみ使用可能とする。それ以外の用紙は受け付けない。欠席したものは講義、もしくは直接配布をうけること。

Ａ(1)：
まず、数式で状態変数の置き換えをします。
提示された式は、
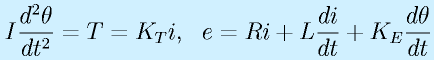
$I\frac{d^2\theta}{dt^2}=T=K_Ti,~~e=Ri+L\frac{di}{dt}+K_E\frac{d\theta}{dt}$
です。状態変数は $\vect{x}=(x_1,x_2,x_3)=(i,\theta,\dot\theta)$ と置きますが、２本目の式のθの微分は、x2の微分ともx3ともおけます。状態方程式では、個々の式で状態変数の微分は左辺の１個のみに制限されていることから、ここではx3と置きます。
$I\dot{x_3}=K_Tx_1,~~~e=Rx_1+L\dot{x_1}+K_Ex_3$
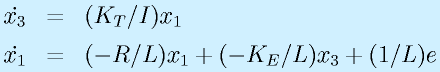
$\dot{x_3}&=&(K_T/I)x_1\nonumber\\\dot{x_1}&=&(-R/L)x_1+(-K_E/L)x_3+(1/L)e$
ここで、状態変数x2に対する状態方程式はありません。これは、状態方程式の講義で最初にもあった例ですが、
$\dot{\theta}=\dot{\theta}$
という式を立て、
$\dot{x_2}=x_3$
と直します。以上を状態方程式の形式にすると、
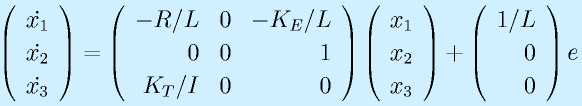
$\Mso{\dot{x_1}}{\dot{x_2}}{\dot{x_3}}=\Mss{-R/L}{0}{-K_E/L}{0}{0}{1}{K_T/I}{0}{0}\Mso{x_1}{x_2}{x_3}+\Mso{1/L}{0}{0}e$
となります。
一方、角度を観測する出力方程式は
$y=\theta=(0~~1~~0)\vect{x}$
となります。

Ａ(2)：
可制御性を確認するには、(B|AB|AAB)の行列をまず求めます。
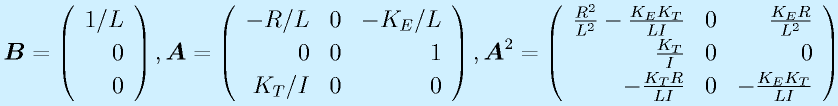
$\vect{B}=\Mso{1/L}{0}{0}, \vect{A}=\Mss{-R/L}{0}{-K_E/L}{0}{0}{1}{K_T/I}{0}{0}, \vect{A}^2=\Mss{\frac{R^2}{L^2}-\frac{K_EK_T}{LI}}{0}{\frac{K_ER}{L^2}}{\frac{K_T}{I}}00{-\frac{K_TR}{LI}}0{-\frac{K_EK_T}{LI}}$
より、
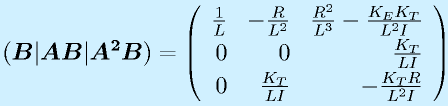
$(\vect{B}|\vect{AB}|\vect{A^2B})=\Mss{\frac{1}{L}}{-\frac{R}{L^2}}{\frac{R^2}{L^3}-\frac{K_EK_T}{L^2I}}{0}{0}{\frac{K_T}{LI}}{0}{\frac{K_T}{LI}}{-\frac{K_TR}{L^2I}}$
となります。一般的に、各定数は正の定数なので、０にはなりません。このままでも明らかですが、２行目、３行目を入れ替えると、３段のそれいじょうつぶせない階段ができますので、rank=3、よって、可制御です。
ちなみに、モータを電圧で操作することは、実際に良く行います。

Ａ(3)：
可観測性を確認するには、(C/CA/CAA)の行列を求めます。
$\vect{C}=(0~~1~~0)$
です。よって、
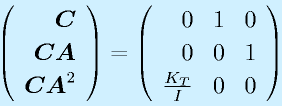
$\Mso{\vect{C}}{\vect{CA}}{\vect{C}\vect{A}^2}=\Mss010001{\frac{K_T}{I}}00$
となり、これも行を並べ替えるとrank=3、よって可観測です。
モータの制御という観点からすると、角度、角速度さえきっちり出せれば、実際には電流は直接的には関係ないように思われますが、モータや電子回路にとって電流はわりと要注意です。あまり強い電流を流すと、そこそこの時間で煙がでてくるのは予想の範囲として、一瞬でも最悪の場合はモータの磁石がダメになることがあります。
一方、可観測ではあるのですが、実際問題として、角度の計測値から角速度を得るのは容易でも、電流まで得ようとすると精度が劣化する可能性が考えられます。このような観点から、モータの性能をフルに発揮させたい場合は、電流のセンサも入れます。電流のセンサ、一番簡単なのは、直列に小さな抵抗をいれることです。