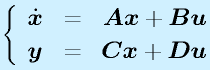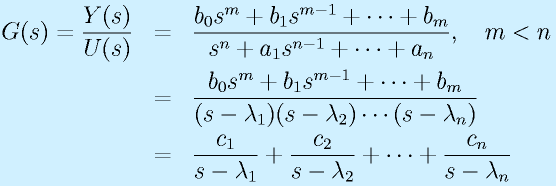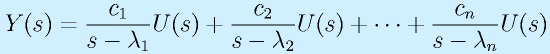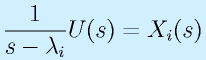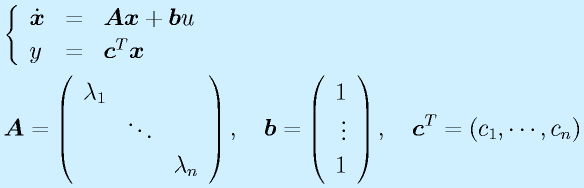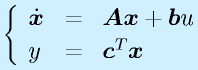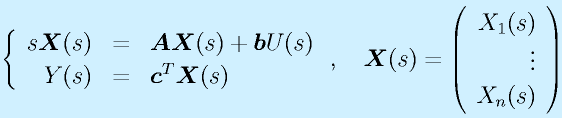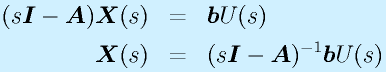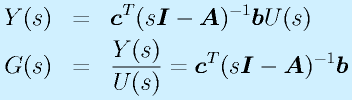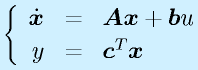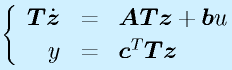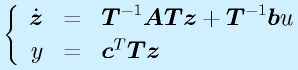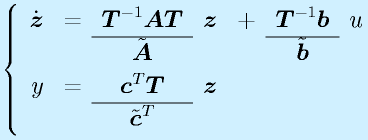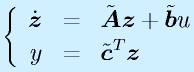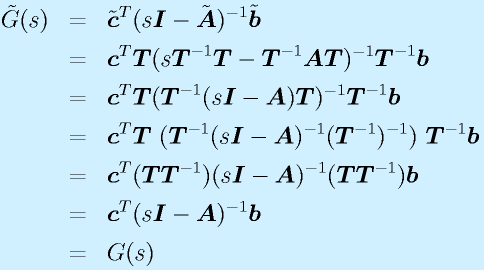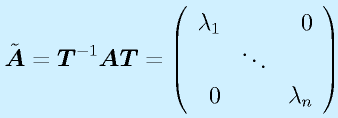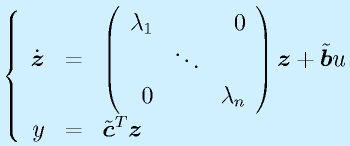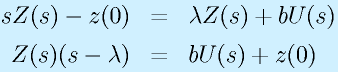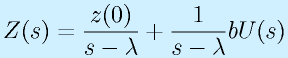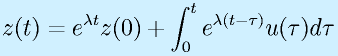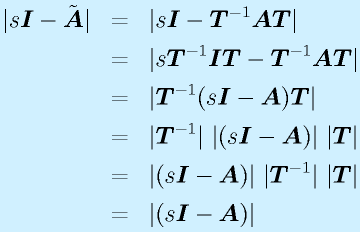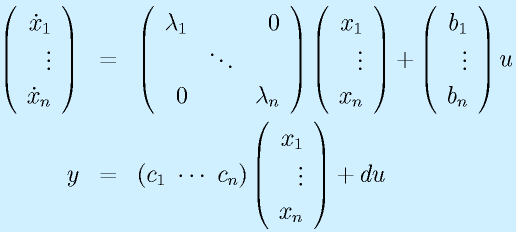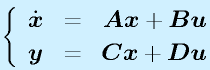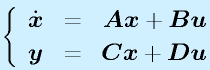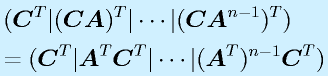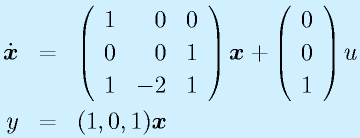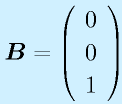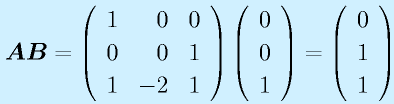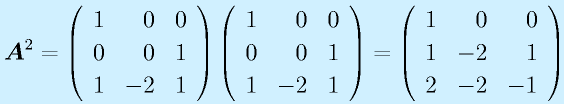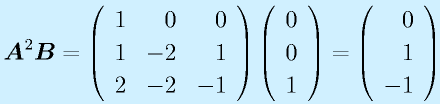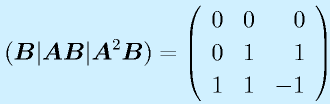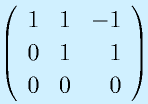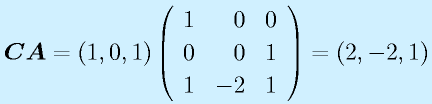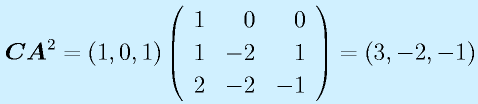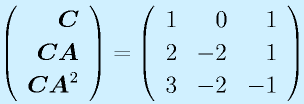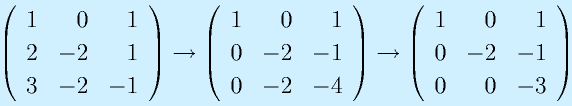状態制御論

制御対象となる線形のシステムは、１階の連立部分方程式で記述できます。

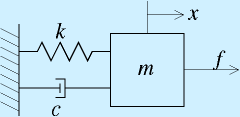
バネ・マス・ダンパ系(右図)を例にします。運動方程式：
$m\ddot{x}+c\dot{x}+kx=f$
(この運動方程式は２階の微分方程式)
ここで、 $v=\dot{x}$ とおくと、
$m\dot{v}+cv+kx=f$
となります。書き換えると
$\begin{array}{cccrc}\dot{x}&=&&v\\ \dot{v}&=&-\frac{k}{m}x&-\frac{c}{m}v&+\frac{1}{m}f\end{array}$
さらに、行列表記にすると、
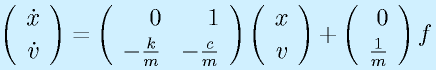
$\Mto{\dot{x}}{\dot{v}}=\Mtt{0}{1}{-\frac{k}{m}}{-\frac{c}{m}}\Mto{x}{v}+\Mto{0}{\frac{1}{m}}f$
となります。ここで、
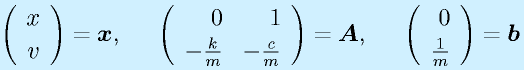
$\Mto{x}{v}=\vect{x},~~~~\Mtt{0}{1}{-\frac{k}{m}}{-\frac{c}{m}}=\vect{A},~~~~ \Mto{0}{\frac{1}{m}}=\vect{b}$
とおくと、
$\dot{\vect{x}}=\vect{A}\vect{x}+\vect{b}f$
という形で表記できます。
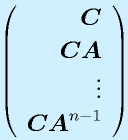
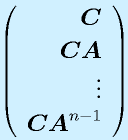
この行列ベクトル形式で表示したシステムの方程式を状態方程式、ベクトル $\vect{x}$ を状態変数といいます。

こういったシステムを実際に作り、観測するとき、必ずしもすべての状態変数が見えるわけでもなく、また単独で見えないこともあります。これを一般的に表記すると、
$y=\vect{c}\vect{x}+df$
と書けます。前半は状態変数が出力にどう出てくるかを示し、後半は入力が観測値に漏れてくる量です(一般にはあまりありませんが、そういうことも想定しておきます)。この方程式を出力方程式と呼びます。

例：上の例で位置が見える場合
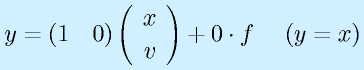
$y=(1~~~0)\Mto{x}{v}+0\cdot f~~~~(y=x)$

以上を一般的な形式で書くと
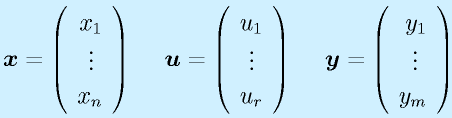
$\vect{x}=\Mso{x_1}{\vdots~}{x_n}~~~~\vect{u}=\Mso{u_1}{\vdots~}{u_r}~~~~\vect{y}=\Mso{y_1}{\vdots~}{y_m}$
(入力x:n要素、出力y:m要素、入力u:r要素)
に対しても、
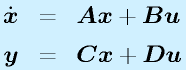
$\dot{\vect{x}}&=&\vect{A}\vect{x}+\vect{B}\vect{u}\nonumber\\\vect{y}&=&\vect{C}\vect{x}+\vect{D}\vect{u}$
となります。ただし、
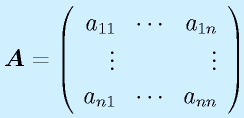$\vect{A}=\Mss{a_{11}}{\cdots}{a_{1n}}{\vdots}{}{\vdots}{a_{n1}}{\cdots}{a_{nn}}$ (n×n)
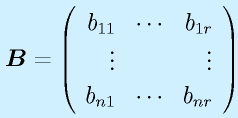$\vect{B}=\Mss{b_{11}}{\cdots}{b_{1r}}{\vdots}{}{\vdots}{b_{n1}}{\cdots}{b_{nr}}$ (n×r)
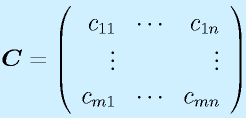$\vect{C}=\Mss{c_{11}}{\cdots}{c_{1n}}{\vdots}{}{\vdots}{c_{m1}}{\cdots}{c_{mn}}$ (m×n)
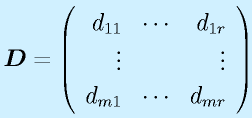$\vect{D}=\Mss{d_{11}}{\cdots}{d_{1r}}{\vdots}{}{\vdots}{d_{m1}}{\cdots}{d_{mr}}$ (m×r)
です。

伝達関数と状態方程式

伝達関数:　
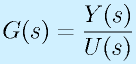$G(s)=\frac{Y(s)}{U(s)}$ ：出力のラプラス変換／入力のラプラス変換
入力から出力までの特性をラプラス変換によって周波数領域で扱います。
状態方程式:　
$\left\{\begin{array}{lcr}\dot{\vect{x}}&=&\vect{A}\vect{x}+\vect{B}\vect{u}\\\vect{y}&=&\vect{C}\vect{x}+\vect{D}\vect{u}\end{array}\right.$
状態を示す状態変数の、１階の連立微分方程式によってシステムを表現し、時間領域で扱います。

どちらも同じ運動方程式などの微分方程式から導かれるため、１入力１出力なシステムでは相互に変換できると期待されます。

伝達関数→状態方程式

一般的なシステムの伝達関数をｓの分数式で表します。
$G(s)=\frac{Y(s)}{U(s)}&=&\frac{b_0s^m+b_1s^{m-1}+\cdots+b_m}{s^n+a_1s^{n-1}+\cdots+a_n},~~~m<n\nonumber\\ &=&\frac{b_0s^m+b_1s^{m-1}+\cdots+b_m}{(s-\lambda_1)(s-\lambda_2)\cdots(s-\lambda_n)}\nonumber\\ &=&\frac{c_1}{s-\lambda_1}+\frac{c_2}{s-\lambda_2}+\cdots+\frac{c_n}{s-\lambda_n}$
(だたし、重解を考えない)
$Y(s)=\frac{c_1}{s-\lambda_1}U(s)+\frac{c_2}{s-\lambda_2}U(s)+\cdots+\frac{c_n}{s-\lambda_n}U(s)$
(λ：極)
ここで、
$\frac{1}{s-\lambda_i}U(s)=X_i(s)$
とおくと、
$X_i(s)(s-\lambda_i)=U(s)$
逆ラプラス変換すると、
$\dot{x}_i(t)-\lambda_ix_i(t)=u(t)$
$\dot{x}_i=\lambda_ix_i+u$
一方、
$y(t)=c_1x_1(t)+c_2x_2(t)+ \cdots +c_nx_n(t)$
なので、合わせると、
$&&\left\{\begin{array}{lcl}\dot{\vect{x}}&=&\vect{A}\vect{x}+\vect{b}u\\y&=&\vect{c}^T\vect{x}\end{array}\right.\nonumber\\ &&\vect{A}=\Mss{\lambda_1}{}{}{}{\ddots}{}{}{}{\lambda_n},~~~\vect{b}=\Mso{1}{\vdots}{1},~~~\vect{c}^T=(c_1, \cdots, c_n)$
となります。これにより、伝達関数が状態方程式に変換できました。

※という形になっても、状態方程式にはできますが、これは後半に純粋な微分を含むため、実在のシステムでは普通はありません。

状態方程式→伝達関数

１入力１出力のｎ次システムの状態方程式、
$\left\{\begin{array}{lcl}\dot{\vect{x}}&=&\vect{A}\vect{x}+\vect{b}u\\y&=&\vect{c}^T\vect{x}\end{array}\right.$
の個々の微分方程式をそのまま, xi(0)=0でラプラス変換します。
※ $x_i\rightarrow X_i(s),~~\dot{x}_i\rightarrow sX_i(s),~~\vect{x}\rightarrow\vect{X}(s)$
$\left\{\begin{array}{rcl}s\vect{X}(s)&=&\vect{A}\vect{X}(s)+\vect{b}U(s)\\ Y(s)&=&\vect{c}^T\vect{X}(s)\end{array}\right.,~~~\vect{X}(s)=\Mso{X_1(s)}{\vdots}{X_n(s)}$
上段の式を変形します。
$(s\vect{I}-\vect{A})\vect{X}(s)&=&\vect{b}U(s)\nonumber\\\vect{X}(s)&=&(s\vect{I}-\vect{A})^{-1}\vect{b}U(s)$
これを下段の式に代入します。
$Y(s)&=&\vect{c}^T(s\vect{I}-\vect{A})^{-1}\vect{b}U(s)\nonumber\\ G(s)&=&\frac{Y(s)}{U(s)}=\vect{c}^T(s\vect{I}-\vect{A})^{-1}\vect{b}$
となります。これにより、状態方程式で表されたシステムが、伝達関数に変換されました。

※ $s\vect{X}(s)=\Mso{sX_1(s)}{\vdots}{sX_n(s)}=\Mss{s}{}{0}{}{\ddots}{}{0}{}{s}\Mso{X_1(s)}{\vdots}{X_n(s)}=s\vect{I}\vect{X}(s)$
※出力方程式に「+du」があった場合、変形過程に付け加えていくと、伝達関数で単に「+d」になります。

状態変数の変換

ここでは、状態変数の選び方を変えることを考えます。
ごく単純には、たとえば、運動方程式の座標をメートル単位で記述していたものをミリ単位にすると値は1000倍になりますが、そのとき方程式はどうかわるか、２次元運動するものを(x,y)で記述していたけど、座標軸の向きを変えてみたくなった(回転)などで、どう変わるか、という問題です(平行移動とかは含まれませんが..)。

具体的には、
$\vect{x}=\vect{T}\vect{z}, ~~~~ \vect{z}=\vect{T}^{-1}\vect{x}$
で表されるような変換を考えます。ここで、ｎ次正方行列Ｔは逆行列がある＝正則であるとします。
Ｔは定数行列なので、
$\dot{\vect{x}}=\vect{T}\dot{\vect{z}}$
であり、１入力１出力のシステム
$\left\{\begin{array}{rcl}\dot{\vect{x}}&=&\vect{A}\vect{x}+\vect{b}u\\y&=&\vect{c}^T\vect{x}\end{array}\right.$
に単に代入すると、
$\left\{\begin{array}{rcl}\vect{T}\dot{\vect{z}}&=&\vect{A}\vect{T}\vect{z}+\vect{b}u\\y&=&\vect{c}^T\vect{T}\vect{z}\end{array}\right.$
上段の式に左からＴの逆行列をかけると、
$\left\{\begin{array}{rcl}\dot{\vect{z}}&=&\vect{T}^{-1}\vect{A}\vect{T}\vect{z}+\vect{T}^{-1}\vect{b}u\\y&=&\vect{c}^T\vect{T}\vect{z}\end{array}\right.$
となります。ここで、
$\left\{\begin{array}{rcccccc}\dot{\vect{z}}&=&\vect{T}^{-1}\vect{A}\vect{T}&\vect{z}&+&\vect{T}^{-1}\vect{b}&u\\\cline{3-3}\cline{6-6} &&\tilde{\vect{A}}&&&\tilde{\vect{b}}\\y&=&\vect{c}^T\vect{T}&\vect{z}\\\cline{3-3} &&\tilde{\vect{c}}^T\end{array}\right.$
と置き換えを行うと、
$\left\{\begin{array}{rcl}\dot{\vect{z}}&=&\tilde{\vect{A}}\vect{z}+\tilde{\vect{b}}u\\y&=&\tilde{\vect{c}}^T\vect{z}\end{array}\right.$
と、一般的な状態方程式の形になります。つまり、正則な行列Ｔをつかって、状態変数を扱いやすいように変換することができます。

ここで、この変換後のシステムの伝達関数を求めてみます。
$\tilde{G}(s)&=&\tilde{\vect{c}}^T(s\vect{I}-\tilde{\vect{A}})^{-1}\tilde{\vect{b}}\nonumber\\ &=& \vect{c}^T\vect{T}(s\vect{T}^{-1}\vect{T}-\vect{T}^{-1}\vect{A}\vect{T})^{-1}\vect{T}^{-1}\vect{b}\nonumber\\ &=& \vect{c}^T\vect{T}(\vect{T}^{-1}(s\vect{I}-\vect{A})\vect{T})^{-1}\vect{T}^{-1}\vect{b} \nonumber\\ &=& \vect{c}^T\vect{T}~(\vect{T}^{-1}(s\vect{I}-\vect{A})^{-1}(\vect{T}^{-1})^{-1})~\vect{T}^{-1}\vect{b} \nonumber\\ &=& \vect{c}^T(\vect{T}\vect{T}^{-1})(s\vect{I}-\vect{A})^{-1}(\vect{T}\vect{T}^{-1})\vect{b} \nonumber\\ &=&\vect{c}^T (s\vect{I}-\vect{A})^{-1}\vect{b} \nonumber\\&=&G(s)$
これは、Ｔによる変換で、伝達関数が変わらないことを意味します。同じシステムで、変数の取り方を変えても、その物理特性が変わるはずはないので、当たり前と言えば当たり前ですが、数学的に確認できました。

このように、解析をしやすくするために状態変数を置き換えることができます。

標準系状態方程式

状態方程式の行列Ａに対して、
$|s\vect{I}-\vect{A}|=0$ , 特性方程式
の解である固有値λiに対応する固有ベクトル v iを用いた座標変換、
$\vect{x}=\vect{Tz},~~~\vect{T}=(\vect{v}_1,\cdots,\vect{v}_n)$
を用いると、固有ベクトルと対角化の関係により、
$\tilde{\vect{A}}=\vect{T}^{-1}\vect{A}\vect{T}=\Mss{\lambda_1}{}{0}{}{\ddots}{}{0}{}{\lambda_n}$
と変換されます。これは状態方程式が、
$\left\{\begin{array}{rcl}\dot{\vect{z}}&=&\Mss{\lambda_1}{}{0}{}{\ddots}{}{0}{}{\lambda_n}\vect{z}+\tilde{\vect{b}}u\\y&=&\tilde{\vect{c}}^T\vect{z}\end{array}\right.$
という形になることを意味します。
(伝達関数を状態方程式にしたときも同形であることを思いだしませう)。

この時、状態方程式部分については、個々の式にばらしてみると
$\dot{z}_i=\lambda_iz_i+b_iu$
と、各状態変数が独立した微分方程式になっています。これは、連立の微分方程式を解く必要もなく、個々の状態変数ごとに解析的に結果を求めることが簡単であることを意味します。
この形を標準系状態方程式、もしくは対角正準系、と呼びます。
なお、固有ベクトルの選び方(個々の固有ベクトルの長さ)でbiをすべて１にすることもできます。

この方程式
$\dot{z}=\lambda z+bu$
を解いてみます。→制御工学Iの教科書のどこか
まず、ラプラス変換。
$sZ(s)-z(0)&=&\lambda Z(s)+bU(s) \nonumber\\ Z(s)(s-\lambda)&=&bU(s)+z(0)$
$Z(s)=\frac{z(0)}{s-\lambda}+\frac{1}{s-\lambda}bU(s)$
ラプラス逆変換して、
$z(t)=e^{\lambda t}z(0)+\int_0^t e^{\lambda(t-\tau)}u(\tau)d\tau$
を得ます。
このλによってz(t)の挙動は大きく変わります。
　λの実部が０未満：安定(たとえば初期値がどんどん０に向う)
　λの実部が０以上：不安定(発振、発散)
ちなみに、λの虚部によって、振動的かどうか、その程度が決まります。

結論としては、システムの行列Ａの固有値は、そのシステムの安定性をみる上で非常に重要である、ということがわかりました。また、システムの中の個々の特徴も直接的に見える数値です。

補足：座標変換と特性方程式
座標変換したシステムの特性方程式を計算してみます。
$|s\vect{I}-\tilde{\vect{A}}|&=&|s\vect{I}-\vect{T}^{-1}\vect{A}\vect{T}|\nonumber\\&=&|s\vect{T}^{-1}\vect{I}\vect{T}-\vect{T}^{-1}\vect{A}\vect{T}|\nonumber\\ &=&|\vect{T}^{-1}(s\vect{I}-\vect{A})\vect{T}|\nonumber\\ &=&|\vect{T}^{-1}|~|(s\vect{I}-\vect{A})|~|\vect{T}|\nonumber\\ &=&|(s\vect{I}-\vect{A})|~|\vect{T}^{-1}|~|\vect{T}|\nonumber\\ &=&|(s\vect{I}-\vect{A})|$
となるため、変数の取り方によって普遍です(直感的に当たり前)。

可制御・可観測

可制御・可観測とは

これまで、制御工学で題材としてきたシステムのほとんどは、入力を与えると物理的に反応があり、結果が検出できることになっていました。しかし、一般的なシステムを考えた場合、必ずしも制御できるとは限りませんし、対象の状態が必ずしも見えるとは限りません。また、一見すると、直接的には操作、観察できない状態であっても、間接的に操作、観察ができるかもしれません。
そういった状況をここでは取り扱います。

例１：
システム
$\Mso{\dot{x}_1}{\vdots}{\dot{x}_n}&=&\Mss{\lambda_1}{}{0}{}{\ddots}{}{0}{}{\lambda_n}\Mso{x_1}{\vdots}{x_n}+\Mso{b_1}{\vdots}{b_n}u \nonumber\\ y&=&(c_1~\cdots~c_n)\Mso{x_1}{\vdots}{x_n}+du$
において、bi、ciについて考える。

$\dot{x}_i=\lambda_ix_i+b_iu$
もし、bi=0だと、 $\dot{x}_i=\lambda_ix_i$ となり、初期値xi(0)と、λiのみによって、xi(t)は規定される＝制御できない。
ａ：λiの実部＜０だと、xiは０に近づく
ｂ：λiの実部＞０だと、xiは発散
ａの場合では、とりあえず０には近づくため、システム全体としては安定といえるが、もし、制御できるならばより早く０に近づけるなどの特性改善が可能。ｂの場合は、発散するため、システムに有害。
$y=c_1x_1+\cdots+c_ix_i+\cdots+c_nx_n$
ci=0だとすると、xiの挙動は一切出力されないため、検出不能。
（ごちゃまぜになってはいても、出力さえされていればなんとか分離できる場合が多い）

例２：

制御観測

スイッチでON/OFFできる、室内の電球 ○ ○

スイッチでON/OFFできる、天井裏の電球 ○ ×

スイッチでON/OFFできない、室内の電球 × ○

スイッチでON/OFFできない、天井裏の電球 × ×

可制御

各状態変数がなんらかの方法で制御できることを「可制御」といいます。
定義：
任意の初期状態 $\vect{x}(0)$ から、与えられた状態 $\vect{x}(t_f)$ へ、何らかの入力 $\vect{u}(t)$ によって、移すことができる
　　→可制御である / controllable

判定法：
$\left\{\begin{array}{lcr}\dot{\vect{x}}&=&\vect{A}\vect{x}+\vect{B}\vect{u}\\\vect{y}&=&\vect{C}\vect{x}+\vect{D}\vect{u}\end{array}\right.$
に対して、行列
$(\vect{B}|\vect{AB}|\vect{A}^2\vect{B}|\cdots|\vect{A}^{n-1}\vect{B})$
の階数(rank)がｎである→「可制御」、「(Ａ、Ｂ)は可制御」

一方、rankがｎ未満であると、不可制御。

可観測

各状態変数がなんらかの方法で検出できることを「可観測」といいます。
定義：
出力 $\vect{y}(t)$ と入力 $\vect{u}(t)$ を０≦t≦tfの期間、観測することで $\vect{x}(0)$ を求めることができる
　　→可観測である / observable

判定法：
$\left\{\begin{array}{lcr}\dot{\vect{x}}&=&\vect{A}\vect{x}+\vect{B}\vect{u}\\\vect{y}&=&\vect{C}\vect{x}+\vect{D}\vect{u}\end{array}\right.$
に対して、行列
$\Mqo{\vect{C}}{\vect{C}\vect{A}}{\vdots}{\vect{C}\vect{A}^{n-1}}$
のrankがｎである→「可観測」「（Ｃ、Ａ）は可観測」

双対性

可観測性の判定行列
$\Mqo{\vect{C}}{\vect{C}\vect{A}}{\vdots}{\vect{C}\vect{A}^{n-1}}$
を転置してみます。
$&&(\vect{C}^T|(\vect{C}\vect{A})^T|\cdots|(\vect{C}\vect{A}^{n-1})^T)\nonumber\\&&=(\vect{C}^T|\vect{A}^T\vect{C}^T|\cdots|(\vect{A}^T)^{n-1}\vect{C}^T)$
これを可制御性の判定行列と見比べてみると、同じ形をしていることが分かります。
　（Ｃ，Ａ）が可観測←→（ＡT，ＣT）が可制御
　（Ａ，Ｂ）が可制御←→（ＢT，ＡT）が可観測
これを双対性といいます。
（あまり、普段はつかいませんが理論証明などで使うことあり）

判定例

システム
$\dot{\vect{x}}&=&\Mss1000011{-2}1\vect{x}+\Mso001u\nonumber\\y&=&(1,0,1)\vect{x}$
の可制御性、可観測性を調べます。

可制御性：
$\vect{B}=\Mso001$ $\vect{AB}=\Mss1000011{-2}1\Mso001=\Mso011$ $\vect{A}^2=\Mss1000011{-2}1 \Mss1000011{-2}1 = \Mss1001{-2}12{-2}{-1}$ $\vect{A}^2\vect{B}=\Mss1001{-2}12{-2}{-1}\Mso001 = \Mso01{-1}$
$(\vect{B}|\vect{AB}|\vect{A}^2\vect{B})=\Mss00001111{-1}$
この行列の１行目と３行目を入れ替えると、
$\Mss11{-1}011000$
となるため、rank=2、よって可制御ではありません。

可観測性：
$\vect{C}=(1,0,1)$
$\vect{C}\vect{A}=(1,0,1)\Mss1000011{-2}1=(2,-2,1)$
$\vect{C}\vect{A}^2=(1,0,1)\Mss1001{-2}12{-2}{-1}=(3,-2,-1)$
$\Mso{\vect{C}}{\vect{CA}}{\vect{CA}^2}=\Mss1012{-2}13{-2}{-1}$
rankを求めます。
$\Mss1012{-2}13{-2}{-1}\rightarrow\Mss1010{-2}{-1}0{-2}{-4}\rightarrow\Mss1010{-2}{-1}00{-3}$
※２行目−１行目×２，３行目−１行目×３、３行目−２行目
rank=3なので、このシステムは可観測です。

別の直感的見方：状態方程式の、Ａに関わる部分だけを見ると、
　x1は、x1によって変化する
　x2は、x3によって変化する
　x3は、x1,x2,x3によって変化する
となっています。入力uはx3に変化を与えるため、x3は直接、x2はx3を経由して変化しますが、x1には何の影響もありません。そう考えると、可制御でなさそうです。
一方、出力はx1とx3が混じっていますので、これらは直接観測されます。x2については、x3を経由して変化が見えると言えます。全部見えるので可観測と考えられます。

このページ、ここまで。

	制御	観測
スイッチでON/OFFできる、室内の電球	○	○
スイッチでON/OFFできる、天井裏の電球	○	×
スイッチでON/OFFできない、室内の電球	×	○
スイッチでON/OFFできない、天井裏の電球	×	×

状態制御論

状態変数と状態方程式

伝達関数と状態方程式

伝達関数と状態方程式

伝達関数→状態方程式

状態方程式→伝達関数

状態変数の変換

状態変数の変換

標準系状態方程式

可制御・可観測

可制御・可観測とは

可制御

可観測

双対性

判定例