状態フィードバックとオブザーバ

状態変数のフィードバック

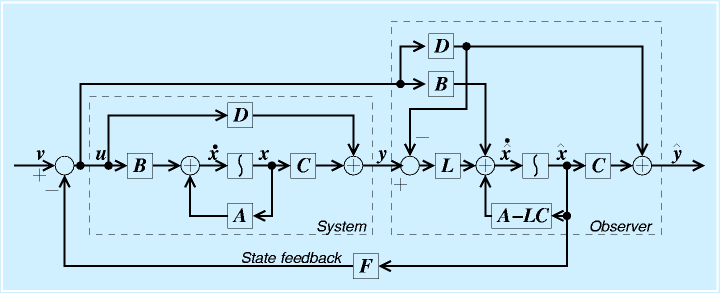
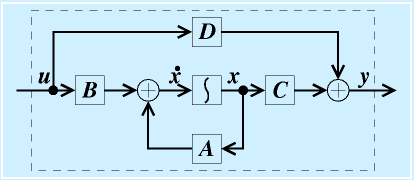制御対象のシステム状態方程式で表したシステム
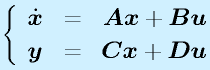
$\left\{\begin{array}{lcr}\dot{\vect{x}}&=&\vect{A}\vect{x}+\vect{B}\vect{u}\\\vect{y}&=&\vect{C}\vect{x}+\vect{D}\vect{u}\end{array}\right.$
をブロック線図で表すと、右図のようになります。古典制御理論では、全体の出力 y を入力に対してフィードバックしました。それに対して、状態制御論におけるフィードバックは、状態変数をフィードバックします。これを状態フィードバックと言います。
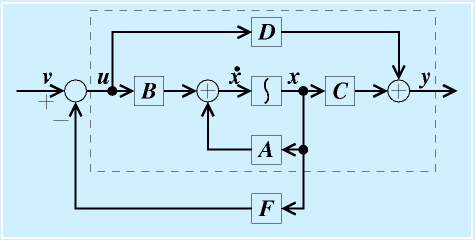具体的には、システムの入力 u に対して、
$\vect{u}=-\vect{Fx}+\vect{v}$
を入力します。 v は u に代わる、新しい入力です。

これを元のシステムの状態方程式、出力方程式に代入します。
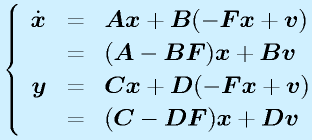
$\left\{\begin{array}{rcl}\dot{\vect{x}}&=&\vect{A}\vect{x}+\vect{B}(-\vect{Fx}+\vect{v})\\&=&(\vect{A}-\vect{BF})\vect{x}+\vect{Bv}\\ \vect{y}&=&\vect{C}\vect{x}+\vect{D}(-\vect{Fx}+\vect{v})\\ &=&(\vect{C}-\vect{DF})\vect{x}+\vect{Dv}\end{array}\right.$
この式を良く見ると、元々 A だったシステム行列が A-BF に置き換えられたシステムになったと見ることができます。

なお、(A,B)が可制御ならば(A-BF,B)も可制御、(C,A)が可観測ならば(C-DF,A-BF)も可観測です。

状態フィードバックと固有値

システムの安定性(収束性)が、システム行列の固有値に依存することはすでに説明しました。特に固有値の実部が負でなければ、そもそも不安定です。
ここでは状態フィードバックによる固有値の変化を調べてみます。

もとのシステムの固有値は、特性方程式
$|s\vect{I}-\vect{A}|=0$
で得られます。状態フィードバックしたシステムの固有値は、
$|s\vect{I}-(\vect{A}-\vect{BF})|=0$
の解です。

ここでは、１入力１出力、２次のシステムを例にその固有値の変化を考えてみます。
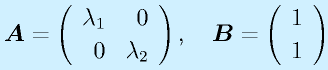
$\vect{A}=\Mtt{\lambda_1}{0}{0}{\lambda_2},~~~\vect{B}=\Mto11$
$\vect{F}=(f_1,f_2)$
とすると、
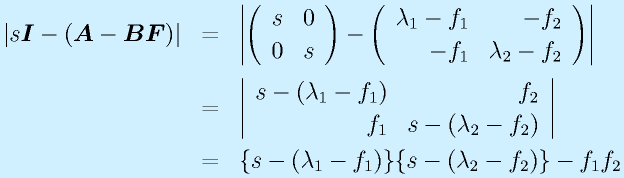
$|s\vect{I}-(\vect{A}-\vect{BF})|&=&\left|\Mtt{s}00s-\Mtt{\lambda_1-f_1}{-f_2}{-f_1}{\lambda_2-f_2}\right|\nonumber\\ &=& \left|\begin{array}{rr} s-(\lambda_1-f_1) & f_2\\f_1&s-(\lambda_2-f_2)\end{array}\right|\nonumber\\&=&\{s-(\lambda_1-f_1)\}\{s-(\lambda_2-f_2)\}-f_1f_2$
$=s^2-\{(\lambda_1-f_1)+(\lambda_2-f_2)\}s+\lambda_1\lambda_2-\lambda_1f_2-\lambda_2f_1=0$
ここで、
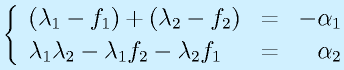
$\left\{\begin{array}{lcr}(\lambda_1-f_1)+(\lambda_2-f_2)&=&-\alpha_1\\\lambda_1\lambda_2-\lambda_1f_2-\lambda_2f_1&=&\alpha_2\end{array}\right.$
とおくと、
$s^2+\alpha_1s+\alpha_2=0$
となります。
一方、
$\left\{\begin{array}{lcr}f_1+f_2&=&\alpha_1+\lambda_1+\lambda_2\\ \lambda_2f_1+\lambda_1f_2&=&-\alpha_2+\lambda_1\lambda_2\end{array}\right.$
なので、λ1≠λ2ならば、α1、α2を指定すれば、f1、f2を求められます(可制御なら、λ1≠λ2)。
よって、

目標とする固有値を決める
α1、α2が求まる ※(s-λ1)(s-λ2)=0より
f1、f2を求める

という手順により、元々の固有値、λ1、λ2を好きな固有値に変更することができます。

状態フィードバックを行うと、可制御なら元のシステムが不安定であっても安定化し、かつ収束の特性も決めることができます。

オブザーバ

状態フィードバックは状態変数がすべて得られることが前提ですが、すべての状態変数を個別に観測できるだけセンサをつけることができるとは限らず、そのままでは使用が非常に制限されます。そこで、制御対象とすっかり同じシステムの数値モデルをつくり、制御対象と平行してシミュレーションし、そのなかの状態変数で代用することを考えます。
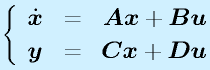
実システム： $\left\{\begin{array}{lcr}\dot{\vect{x}}&=&\vect{A}\vect{x}+\vect{B}\vect{u}\\\vect{y}&=&\vect{C}\vect{x}+\vect{D}\vect{u}\end{array}\right.$
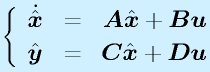
シミュレータ： $\left\{\begin{array}{lcr}\dot{\hat{\vect{x}}}&=&\vect{A}\hat{\vect{x}}+\vect{B}\vect{u}\\\hat{\vect{y}}&=&\vect{C}\hat{\vect{x}}+\vect{D}\vect{u}\end{array}\right.$
実システムとシミュレータでは各パラメータは同一、ただし、状態変数と出力は異なります。
ここで、誤差 $\vect{e}=\hat{\vect{x}}-\vect{x}$ を考えます。
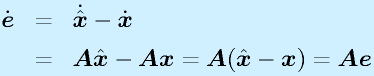
$\dot{\vect{e}}&=&\dot{\hat{\vect{x}}}-\dot{\vect{x}}\nonumber\\ &=&\vect{A}\hat{\vect{x}}-\vect{Ax}=\vect{A}(\hat{\vect{x}}-\vect{x})=\vect{Ae}$
よって、もし A が安定なら、一応収束します。ただし、 A が不安定な場合は収束しませんし、収束の具合いもシステムまかせです。

そこで、実際の出力とシミュレータの出力の差を、シミュレータにフィードバックしてみます。
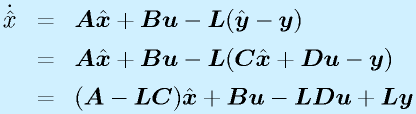
$\dot{\hat{x}}&=&\vect{A}\hat{\vect{x}}+\vect{Bu}-\vect{L}(\hat{\vect{y}}-\vect{y})\nonumber\\ &=&\vect{A}\hat{\vect{x}}+\vect{Bu}-\vect{L}(\vect{C}\hat{\vect{x}}+\vect{Du}-\vect{y}) \nonumber\\ &=&(\vect{A}-\vect{LC})\hat{\vect{x}}+\vect{Bu}-\vect{LDu}+\vect{Ly}$
このとき、改めて誤差を計算すると、
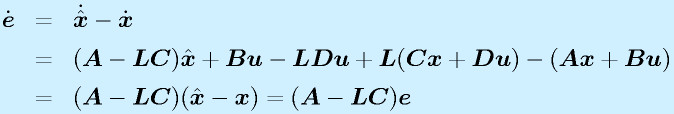
$\dot{\vect{e}}&=&\dot{\hat{\vect{x}}}-\dot{\vect{x}}\nonumber\\ &=&(\vect{A}-\vect{LC})\hat{\vect{x}}+\vect{Bu}-\vect{LDu}+\vect{L}(\vect{Cx}+\vect{Du})-(\vect{Ax}+\vect{Bu}) \nonumber\\ &=&(\vect{A}-\vect{LC})(\hat{\vect{x}}-\vect{x})=(\vect{A}-\vect{LC})\vect{e}$
となります。
これは、誤差 e が、行列 A ではなく、( A-LC )によって収束することを意味します。よって、状態フィードバックで示したのと同様に L の固有値を決定することにより、実システムとシミュレータの間の誤差を、システムが不安定であっても、収束させることができます。
ただし、今度は、(C,A)が可制御である必要があります。

簡単にオブザーバの設計法をまとめます。

$(\vect{C},\vect{A})$ が可観測ならば、 $(\vect{A}^T,\vect{C}^T)$ が可制御なので(双対性)、 $\vect{A}^T-\vect{C}^T\vect{F}$ の固有値を自由に設定できる(状態フィードバック)。
$(\vect{A}-\vect{LC})$ の固有値と $(\vect{A}-\vect{LC})^T$ の固有値は等しく、
$(\vect{A}-\vect{LC})^T=\vect{A}^T-(\vect{LC})^T=\vect{A}^T-\vect{C}^T\vect{L}^T$
なので、 $\vect{A}^T\rightarrow\vect{A},~~\vect{C}^T\rightarrow\vect{B}$ と置き換えて、 $\vect{A}-\vect{BF}$ の状態フィードバック系を設計する。
得られた $\vect{F}$ より、 $\vect{L}=\vect{F}^T$ とすることで、 $\vect{A}-\vect{LC}$ の固有値を設定できる。

これにより、実システムがモデル化できれば、オブザーバをつくり、状態変数を推定することが可能となります。オブザーバ＋状態フィードバック

最適制御

この節では最適制御とよばれる、状態フィードバックの設計手法について述べます。状態フィードバックでは行列Ｆを指定することで、固有値の位置をずらすことができました。ただ、固有値の位置というのは、設計上、直感的には分かりにくい修正です。また、その設計も次数が上がると大変です。
それに対して、最適制御では「評価の仕方」を与えることで、その条件で「最適」なＦを得ることができます。

最適とはなにか

制御において最適とはなんでしょうか。

状態変数が小さい。
入力が小さい。
状態変数の収束が早い。
入力が平均的に小さい。
変化がおだやか。
目標到達時間が短い

など、様々な要求があります。それぞれの要求に対して最適といえるパラメータがありそうなので、まず、評価方法を決めます。
例１：
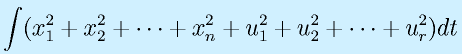
$\int(x_1^2+x_2^2+\cdots+x_n^2+u_1^2+u_2^2+\cdots+u_r^2)dt$
を最小にするようにする。

この条件の意味は、

x:制御量 u:操作出力
積分：状態変数および入力(フィードバック分)が収束するまでの状態量、操作をすべて評価に入れる。
x,uの２乗：負にならない値で評価。０から正になっても負になっても大きな値となる。
|x|, |u| でも意味は変わらないが、数学的な処理の過程で、微分するときに絶対値は面倒。x^2なら微分できる。
c.f. 最小自乗法

です。つまり、全部の状態量、入力が、動作全般にわたって小さくなるようにするという意味を持ちます。
ここで、重みを付けられるように改良します。
例２：
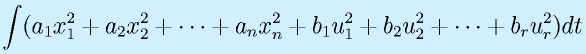
$\int(a_1x_1^2+a_2x_2^2+\cdots+a_nx_n^2+b_1u_1^2+b_2u_2^2+\cdots+b_ru_r^2)dt$
を最小にするようにする。

重みを付けた。
a1を１０倍すると、当然x1が重視され、x1を他より優先して小さくするようになる。

考え方によって、「最適」を表す方法はいくらでもあると言えますが、ここではこの後者の式を基本に考えます。

最適制御(最適レギュレータ)

システム、
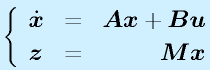$\left\{\begin{array}{lcr}\dot{\vect{x}}&=&\vect{A}\vect{x}+\vect{B}\vect{u}\\\vect{z}&=&\vect{M}\vect{x}\end{array}\right.$ (z: 仮想的出力)
に対して、評価値
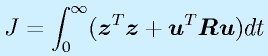
$J=\int_0^\infty(\vect{z}^T\vect{z}+\vect{u}^T\vect{R}\vect{u})dt$
を最小とする状態フィードバックを求めてみます。
＝Ｍによってxを、Ｒによってuを評価します。

解(天下り)：
$\vect{u}=-\vect{Fx}=-\vect{R}^{-1}\vect{B}^T\vect{Px}$
を状態フィードバックします。ここで、Ｐは、
$\vect{A}^T\vect{P}+\vect{P}\vect{A}+\vect{M}^T\vect{M}-\vect{PBR}^{-1}\vect{B}^T\vect{P}=\vect{0}$ ：リカティ方程式
の解です(n次正方、正定対称)。

あるいは、 $\vect{z}^T\vect{z}=\vect{x}^T\vect{M}^T\vect{Mx}$ なので、 $\vect{M}^T\vect{M}=\vect{Q}$ と置いて、
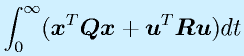
$\int_0^\infty(\vect{x}^T\vect{Qx}+\vect{u}^T\vect{Ru})dt$
を最小にするという表現もあります。
ここで、Ｒは正定対称行列、Ｑは半正定対称行列です。
※正定：０以外の任意の $\vect{x}$ に対して、 $\vect{x}^T\vect{Qx}>0$ となること。
※半正定：０位外の任意の $\vect{x}$ に対して、 $\vect{x}^T\vect{Qx}\geq0$ となること。

このようにして得た状態フィードバック系は、(A,B)が可制御、(M,A)が可観測なら必ず安定します。
１入力１出力のシステムに対して、一巡伝達関数を求め、ナイキスト線図を書くと、かならず-1+0iを中心とする半径１の円の外側を通って、０に行きます。これは、
「ゲイン余裕∞」「位相余裕６０度以上」
を意味します(かなり安定)。

なお、このとき、評価値は
$J=\vect{x}(0)^T\vect{P}\vect{x(0)}$
となります。

リカティ方程式 $\vect{A}^T\vect{P}+\vect{P}\vect{A}+\vect{Q}-\vect{PBR}^{-1}\vect{B}^T\vect{P}=\vect{0}$ の解き方：

力業で直接Ｐの要素を求める(実用的ではない)
$-\dot{\vect{P}}=\vect{A}^T\vect{P}+\vect{P}\vect{A}+\vect{Q}-\vect{PBR}^{-1}\vect{B}^T\vect{P}$
をP(0)=0を初期値として、ｔ→−∞方向に数値計算していくと、いずれ収束して $-\dot{\vect{P}}=\vect{0}$ となり、リカティ方程式の解が得られる。
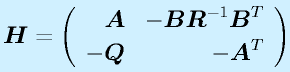$\vect{H}=\Mtt{\vect{A}}{-\vect{B}\vect{R}^{-1}\vect{B}^T}{-\vect{Q}}{-\vect{A}^T}$ (2n×2n)
の固有値(2n個)を求め、そのうち、実部が負のもの(必ずｎ個あり)λ1…λnに対する固有ベクトルを求める。
固有ベクトルをｎ次ベクトル２個に切り離すことができ、
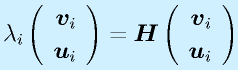
$\lambda_i\Mto{\vect{v}_i}{\vect{u}_i}=\vect{H}\Mto{\vect{v}_i}{\vect{u}_i}$
と、なるとき、
$\vect{P}=[\vect{u}_1\cdots\vect{u}_n][\vect{v}_1\cdots\vect{v}_n]^{-1}$ で、計算できます。

素手で最適制御を計算してみる

システム
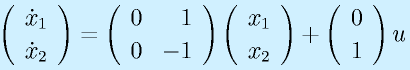
$\Mto{\dot{x}_1}{\dot{x}_2}=\Mtt{0}{1}{0}{-1}\Mto{x_1}{x_2}+\Mto01u$
に対して、評価関数
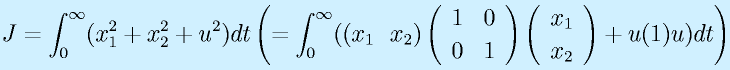
$J=\int_0^\infty(x_1^2+x_2^2+u^2)dt\left(=\int_0^\infty((x_1~~x_2)\Mtt1001\Mto{x_1}{x_2}+u(1)u)dt\right)$
を最小にする最適制御系を求めてみます。

まず、行列：
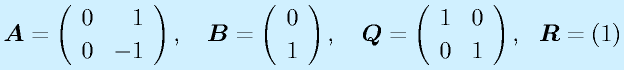
$\vect{A}=\Mtt010{-1},~~~\vect{B}=\Mto01,~~~\vect{Q}=\Mtt1001,~~\vect{R}=(1)$
次に、リカティ方程式
$\vect{A}^T\vect{P}+\vect{P}\vect{A}+\vect{Q}-\vect{PBR}^{-1}\vect{B}^T\vect{P}=\vect{0}$
を解きます。
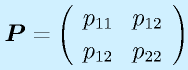$\vect{P}=\Mtt{p_{11}}{p_{12}}{p_{12}}{p_{22}}$ (正定対称)として、
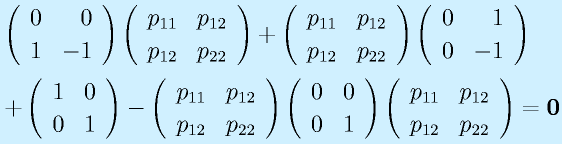
$&&\Mtt001{-1}\Mtt{p_{11}}{p_{12}}{p_{12}}{p_{22}}+\Mtt{p_{11}}{p_{12}}{p_{12}}{p_{22}}\Mtt010{-1}\nonumber\\&&+\Mtt1001-\Mtt{p_{11}}{p_{12}}{p_{12}}{p_{22}}\Mtt0001\Mtt{p_{11}}{p_{12}}{p_{12}}{p_{22}}=\vect{0}$
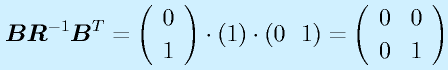
※ $\vect{B}\vect{R}^{-1}\vect{B}^T=\Mto01\cdot(1)\cdot(0~~1)=\Mtt0001$
※ $\vect{R}^{-1}=(-1)^{-1}=(1)$

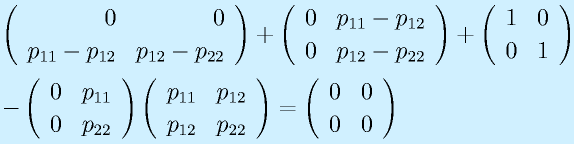
$&&\Mtt00{p_{11}-p_{12}}{p_{12}-p_{22}}+\Mtt0{p_{11}-p_{12}}0{p_{12}-p_{22}}+\Mtt1001\nonumber\\&&-\Mtt0{p_{11}}0{p_{22}}\Mtt{p_{11}}{p_{12}}{p_{12}}{p_{22}}=\Mtt0000$
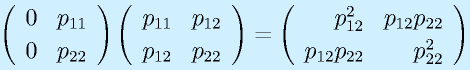
$\Mtt0{p_{11}}0{p_{22}}\Mtt{p_{11}}{p_{12}}{p_{12}}{p_{22}}=\Mtt{p_{12}^2}{p_{12}p_{22}}{p_{12}p_{22}}{p_{22}^2}$

以上とりまとめて
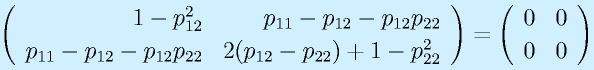
$\Mtt{1-p_{12}^2}{p_{11}-p_{12}-p_{12}p_{22}}{p_{11}-p_{12}-p_{12}p_{22}}{2(p_{12}-p_{22})+1-p_{22}^2}=\Mtt0000$
となります。

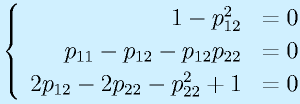
$\left\{\begin{array}{rl}1-p_{12}^2&=0\\ p_{11}-p_{12}-p_{12}p_{22}&=0\\ 2p_{12}-2p_{22}-p_{22}^2+1&=0\end{array}\right.$
１式目より、p12=+-1ですが、Ｐは正定である必要があるため、とりあえず、無難にp12=+1を仮定します。

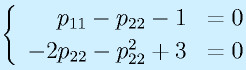
$\left\{\begin{array}{rl}p_{11}-p_{22}-1&=0\\ -2p_{22}-p_{22}^2+3&=0\end{array}\right.$
２式目より、
$p_{22}^2+2p_{22}-3=(p_{22}+3)(p_{22}-1)=0$
なので、p22=-3,1 。同じく、とりあえず、p22=1とします。
すると、１式目よりp11=2になります。

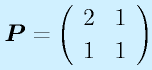
仮に出したＰは $\vect{P}=\Mtt2111$
です。ここで正定性の確認をします。
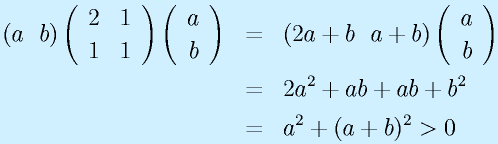
$(a~~b)\Mtt2111\Mto{a}{b}&=&(2a+b~~a+b)\Mto{a}{b}\nonumber\\&=&2a^2+ab+ab+b^2\nonumber\\&=&a^2+(a+b)^2>0$
よって、正定です。
※他のパターン、p12=-1やp22=-3は正定になりません。

よって、
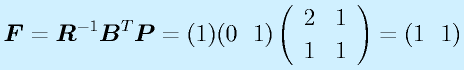
$\vect{F}=\vect{R}^{-1}\vect{B}^T\vect{P}=(1)(0~~1)\Mtt2111=(1~~1)$
を状態フィードバックします。
このとき、状態フィードバックによって
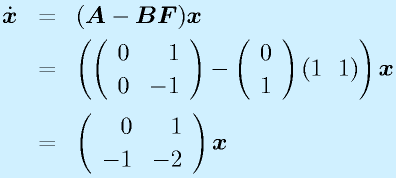
$\dot{\vect{x}}&=&(\vect{A}-\vect{BF})\vect{x}\nonumber\\ &=&\left(\Mtt010{-1}-\Mto01(1~~1)\right)\vect{x}\nonumber\\ &=&\Mtt01{-1}{-2}\vect{x}$
となります。このときの固有値は
$|s\vect{I}-\vect{A}|=s(s+2)+1=s^2+2s+1=(s+1)^2=0$
よって、固有値は(-1)の重解になっています。

以上。

リカティ方程式の解き方その３解説

最適制御により状態フィードバックされたシステムの行列は、
$\vect{A}-\vect{BF}=\vect{A}-\vect{BR}^{-1}\vect{B}^T\vect{P}$
となります。この行列の固有値をλi、固有ベクトルをvi(i=1...n)とすると、その定義より、
$(\vect{A}-\vect{BR}^{-1}\vect{B}^T\vect{P})\vect{v}_i=\lambda_i\vect{v}_i$ もしくは
$(\lambda_i\vect{I}-\vect{A}+\vect{BR}^{-1}\vect{B}^T\vect{P})\vect{v}_i=\vect{0}$ …(1)
となります。

一方、リカティ方程式、
$\vect{A}^T\vect{P}+\vect{P}\vect{A}+\vect{Q}-\vect{PBR}^{-1}\vect{B}^T\vect{P}=\vect{0}$
を変形します。
$(s\vect{I}+\vect{A}^T)\vect{P}-\vect{P}(s\vect{I}-\vect{A}+\vect{BR}^{-1}\vect{B}^T\vect{P})+\vect{Q}=\vect{0}$
これに右からviをかけ、s=λiとすると、
$(\lambda_i\vect{I}+\vect{A}^T)\vect{P}\vect{v}_i-\vect{P}(\lambda_i\vect{I}-\vect{A}+\vect{BR}^{-1}\vect{B}^T\vect{P})\vect{v}_i+\vect{Q}\vect{v}_i=\vect{0}$
ここで、第２項は上の(1)式で０となっているので、
$(\lambda_i\vect{I}+\vect{A}^T)\vect{P}\vect{v}_i+\vect{Q}\vect{v}_i=\vect{0}$
となります。

また(1)式より、
$\vect{A}\vect{v}_i-\vect{BR}^{-1}\vect{B}^T(\vect{Pv}_i)=\lambda_i\vect{v}_i$
２式並べると、
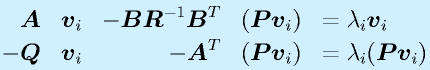
$\begin{array}{rlrll}\vect{A}&\vect{v}_i&-\vect{BR}^{-1}\vect{B}^T&(\vect{Pv}_i)&=\lambda_i\vect{v}_i\\ -\vect{Q}&\vect{v}_i&-\vect{A}^T&(\vect{Pv}_i)&=\lambda_i(\vect{Pv}_i)\end{array}$
となるので、
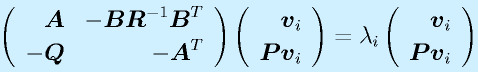
$\Mtt{\vect{A}}{-\vect{BR}^{-1}\vect{B}^T}{-\vect{Q}}{-\vect{A}^T}\Mto{\vect{v}_i}{\vect{Pv}_i}=\lambda_i\Mto{\vect{v}_i}{\vect{Pv}_i}$
となります。

ここで、解き方その３と見比べると、その３で"ui"とされていたものは、"Pvi"に他なりません。これを並べると、
$\vect{P}[\vect{v}_1~~\vect{v}_2~~\cdots~~\vect{v}_n]=[\vect{u}_1~~\vect{u}_2~~\cdots~~\vect{u}_n]\nonumber\\\vect{P}=[\vect{u}_1~~\vect{u}_2~~\cdots~~\vect{u}_n][\vect{v}_1~~\vect{v}_2~~\cdots~~\vect{v}_n]^{-1}$
が得られます。

最適推定

最適推定とは

前に、状態フィードバックを行うために、状態変数観測器オブザーバを使うという方法を示しましたが、これも補正用の行列Ｌを何らかの方法で決める必要があります。その際に、「観測時には(センサには)ノイズが付き物。その影響をなるべく受けなくする」ことを狙った設計が最適推定です。

最適制御に比べると話がややこしいので概略だけ示します。

カルマンフィルタ

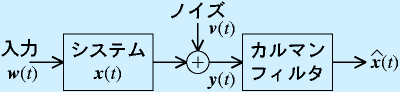カルマンフィルタ概要推定する対象となるシステムには、センサで観測するときにノイズが混じっているものとします。また、入力は任意で、何が入るかわからないとします。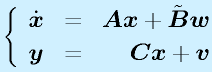
$\left\{\begin{array}{lcr}\dot{\vect{x}}&=&\vect{A}\vect{x}+\tilde{\vect{B}}\vect{w}\\\vect{y}&=&\vect{C}\vect{x}+\vect{v}\end{array}\right.$
ここで、w,uはホワイトノイズ(白色雑音)、すなわち、全周波数の信号を等しく含むランダムな信号とします。また、

同じ制御を何回もやったときに、入力w(t)のそれぞれの回の時刻tでの値の平均値(期待値)はゼロ。
$E[\vect{w}(t)]=\vect{0}$
入力はwは何回やってもどの時刻でも、さらに各要素間でも関連性はなし。
$Cov[\vect{w}(t), \vect{w}(\tau)]=\vect{I}\delta(t-\tau)$
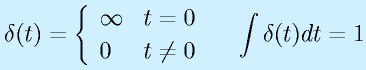
$\delta(t)=\left\{\begin{array}{ll}\infty&t=0\\0&t\neq0\end{array}\right.~~~\int\delta(t)dt=1$
同じく、観測ノイズv(t)も各回の平均はゼロ。
$E[\vect{v}(t)]=\vect{0}$
ただし、v(t)は、時間に関しては、相関性無くランダムでも、各要素間にはある程度関連性あり。 $Cov[\vect{v}(t), \vect{v}(\tau)]=\vect{V}\delta(t-\tau)$

とします。一般的にいって、外乱はランダムにはいるもの、観測ノイズの場合は、たとえばセンサの取りつけがずれているとか、そういった要因で関連したノイズが観測されることがあります。

このような、ある癖を持ったノイズがセンサ出力が混じるシステムに、任意の信号が入る状態で
$\varepsilon(t)=E[(\vect{x}(t)-\hat{\vect{x}}(t))^T(\vect{x}(t)-\hat{\vect{x}}(t))]=0$
つまり、
$\sum\{x_i(t)-\hat{x_i}(t)\}^2$ の平均値が０
となるオブザーバを考えます。

結論：
(A,B)が可制御、(C,A)が可観測の時、
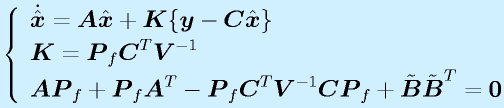
$\left\{\begin{array}{l}\dot{\hat{\vect{x}}}=\vect{A}\hat{\vect{x}}+\vect{K}\{\vect{y}-\vect{C}\hat{\vect{x}}\} \\\vect{K}=\vect{P}_f\vect{C}^T\vect{V}^{-1}\\ \vect{AP}_f+\vect{P}_f\vect{A}^T-\vect{P}_f\vect{C}^T\vect{V}^{-1}\vect{CP}_f+\tilde{\vect{B}}\tilde{\vect{B}}^T=\vect{0}\end{array}\right.$
でオブザーバをつくります。(２本目はリカティ方程式)

最適レギュレータのリカティ方程式と見比べると、
$\vect{A}\rightarrow\vect{A}^T,~~\vect{C}\rightarrow\vect{B}^T,~~\vect{V}\rightarrow\vect{R},~~\tilde{\vect{B}}\tilde{\vect{B}}^T\rightarrow\vect{Q}$
と置き換えれば同じになることが確認できます。これもまた双対性で、リカティ方程式の解き方としては同じになります。

ＬＱＧコントローラ

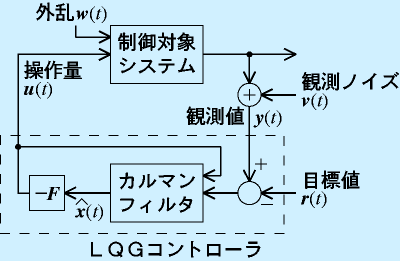LQGコントローラ概要 LQG(Linear-Quadratic-Gaussian)コントローラは最適制御とカルマンフィルタを合体させたフィードバック制御系です。制御対象の出力からカルマンフィルタで状態変数を推定し、それで状態フィードバックをかけます。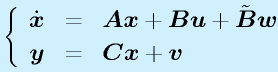

具体的には
$\left\{\begin{array}{rcl}\dot{\vect{x}}&=&\vect{Ax}+\vect{Bu}+\tilde{\vect{B}}\vect{w}\\\vect{y}&=&\vect{Cx}+\vect{v}\end{array}\right.$
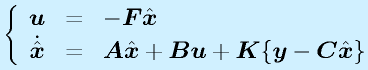$\left\{\begin{array}{rcl}\vect{u}&=&-\vect{F}\hat{\vect{x}}\\ \dot{\hat{\vect{x}}}&=&\vect{A}\hat{\vect{x}}+\vect{Bu}+\vect{K}\{\vect{y}-\vect{C}\hat{\vect{x}}\}\end{array}\right.$ (最適制御/カルマンフィルタ)
という制御式を立てます。

このままでは目標値の入力ができないため、最終的にブロック図で表すと右のようにします。目標値をいれるところを良く見ると、古典制御で目標値をいれる場所(出力と目標値の差)と同じであることがわかります。
なお、最適制御、カルマンフィルタともに古典制御に比べたら圧倒的に強力ですが、２個組み合わせるとそうとも言えなくなるそうです。それでも古典制御に比べたら強力なのはたしかです。