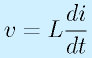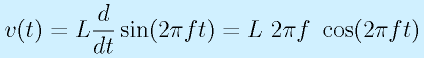電子回路の基礎
[| ]
最終更新: 2012/10/09 10:40:47
電子回路の物理量
電子回路を扱うに辺り、基本となる物理量は電圧と電流です。
たとえば、力学では長さや位置、速度、加速度、力といったもの、流体では流速や圧力などに着目して現象をみたり解析したりします。
電子回路でも様々な物理量を相手にしますが、その中の基本中の基本は 電圧 と 電流 です。
よく、電子回路は水の流れにたとえられます。電圧は水圧に、電流は流量にたとえられます。
さらに、このあとすぐに出てくる 抵抗 は、流体的な抵抗、たとえば、パイプの太さにたとえられます。
同じ太さのパイプに水を流す場合、水圧を高くするほど流量は増えます。同じように、普通は電圧を上げると電流が増えます。
同じ圧力の場合、パイプを太くすると流量は増えます。同じように、抵抗を小さくすると電流が増えます。
ちなみに、水の場合は水の分子が流れます。電流の場合、一般には電子が(逆向きに)流れます。
流体で圧力と流量の関係は「流れる場所の入り口の圧力と出口の圧力の差」が重要です。同じように、電子回路でも重要なのは電流が流れる部品の入口と出口(両端)の電圧です。
細かく言うと、電子回路上のすべての点で、「電位」という値が定義されます。この電位の差(電位差)が電圧として定義されています。
電圧は「2個所の差」なので、本来1個所の電圧というものは規定できません。
ところが、この講義も含めて、慣例的に、「この点の電圧は○○」という表現をよくします。
これは、電子回路を取り扱うときに、基準となる電位を一カ所きめて、そこに対してどれだけの電位差があるかを表すためです。
この基準は様々に呼ばれます。ポピュラーな表現はGND(ground)です。よく、「アースする」といいますが、これは回路のどこかの点を地面に埋めた銅棒などに接続し、その点の電位を地球の電位に一致させることを意味します。そこから、基準となるところを「アース」とか「グランド」と言いました。ただ、最近はアースしないことが一般的で、より汎用な言葉として「コモン」(共通の意味)という呼び方があります。
どちらも同じ「電圧」と読み書きしますが、本来の電圧は「○○(抵抗)にかかる電圧」、基準点からの電圧は「○○(この点)の電圧」と若干表現が異なるので注意しましょう。
電圧、電流も含めた、単位などを以下の表に示します。
| 名称 | よく使われる記号 | 単位 | 説明・定義 | 備考 |
| 電圧、電位差 | E,e,V,v | [V] (ボルト) | | 電池発明のボルタさんより |
| 電流 | I,i | [A] (アンペア) | | 電流と磁界の関係を調べたアンペールさんより |
| (電気)抵抗 | R | [Ω] (オーム) | 対象に電圧Eがかかって電流Iが流れているとき、R=E/I | 基本法則であるオームの法則を発見したオームさんより |
| 電力 | P | [W] (ワット) | ある部品(or回路)に電圧Eがかかっていて、電流Iが流れているとき、P=EI、いわゆる消費電力 | 力学の仕事率と同じ、蒸気機関のワットさん |
| 電気量、電荷 | Q | [C] (クーロン) | 電気(電子)の量。電流を時間で積分したもの。 | 静電気の研究をしたクーロンさん |
| (電気)容量 | C | [F] (ファラッド) | コンデンサの大きさ?を表す | 電気、磁気、化学でいろいろな功績のあるファラデーさんより |
| インダクタンス(誘導係数) | L,M | [H] (ヘンリー) | コイルの大きさ?を表す | 電磁気学の研究をしたらしいヘンリーさんより |
| 周波数 | f | [Hz] (へルツ) | 1秒間の回数を表す | 電磁波の送受信に成功したへルツさんより |
| | | | | |
※記号で表すとき、大文字小文字両者があるものは、一般に時間とともにほぼ変化しないことを主張する場合に大文字、時間変化することを主張する場合に小文字を使うことが多い。
接頭語
上記の主に使用する単位に加えて、接頭語(SI接頭語、SI接頭辞、倍数接頭語)が頻繁に出てきます。接頭語というと聞き慣れないかもしれませんが、「キロ」とか「メガ」といったらおなじみでしょう。全部で、10の24乗から10のマイナス24乗まで20種類がありますが(参考)、以下にこの科目でよく使う物を列挙します。
| 文字 | 読み | 数値 | 使われる対象、備考 |
| k | キロ | 1000倍 | 抵抗値、周波数、電力、電圧 |
| M | メガ(メグ) | 10の6乗=100万倍 | 抵抗値(その場合のみ「メグオーム」と読む場合がある)、周波数 |
| m | ミリ | 1/1000 | 時間、電圧、電流、電力、インダクタンス |
| μ(u) | マイクロ | 10のマイナス6乗、100万分の1 | 電気容量、インダクタンス、時間、電圧、電流、μはギリシア文字で扱いづらいため、uで代替することがある |
| p | ピコ | 10のマイナス12乗 | 電気容量 |
| 以下は本講義ではたぶん扱わないものの電気関係でそこそこ使われるもの |
| G | ギガ | 10の9乗=10億倍 | 周波数 |
| T | テラ | 10の12乗 | 周波数 |
| n | ナノ | 10のマイナス9乗 | 電気容量 |
| 以下は雑学 |
| K | キロ | 2の10乗=1024倍 | コンピュータの世界(主に容量)でのキロ。大文字。1000を大文字で書かないこと |
| M(Mi) | メガ(メビ) | 2の20乗 | コンピュータの世界でのメガ |
| G(Gi) | ギガ(ギビ) | 2の30乗 | コンピュータの世界でのギガ |
| T(Ti) | テラ(テビ) | 2の40乗 | コンピュータの世界でのテラ |
| c | センチ | 1/100 | おなじみセンチメートル。輸入物の缶ジュースなどでcl、センチリットルという書き方有り |
| d | デシ | 1/10 | 小学校以来つかっていないデシリットル、制御などで出てくるデシベル |
| h | ヘクト | 100倍 | ヘクトパスカルで一躍有名に。面積を表すヘクタールはヘクト+アールなのでha。<アールはラテン語の面積(area)かららしい。 |
| da | デカ | 10倍 | 適用例が長いこと見られなかったが、daN(デカニュートン)としての使用が見られる。ほぼ[daN]=[kgf]となるため使われていると推定。 |
接頭語付きでよく使うもの
- 抵抗:Ω、kΩ、MΩ(オーム、キロオーム、メガオーム/メグオーム)
- 容量:μF(uF)、pF(マイクロファラッド、ピコファラッド)
※回路で日常的には接頭語無しのF(ファラッド)は出てこない。
- 時間:ms、μs(us) (ミリ秒/ミリセック、マイクロ秒/マイクロセック)
- 電圧:V、mV、kV (ボルト、ミリボルト、キロボルト)
- 電流:A、mA (アンペア、ミリアンペア)
- 周波数:Hz、kHz、MHz、GHz、THz(ヘルツ、キロヘルツ...)
ただ、これらは正式な表記です。日常的には、単位そのものが明らかな場合、この接頭語だけを言う場合があります。また、回路図で数値だけ、数値+倍数だけで書くことも良くあります。
例:
- 100オームの抵抗(100の抵抗とは言わない)、10キロ(オーム)の抵抗、1メガの抵抗
- 10マイクロのコンデンサ、1000ピコのコンデンサ
- このラジオ局の周波数は1260キロ
- 長さ10ミリ <これも正しくは10ミリメートル
- 電圧、電流はあまり省略することはありません
もちろん、試験の時には正しく表記しましょう。
直流と交流
電圧、電流ともに、「直流」と「交流」という種類があります。
直流は、時間変化の無い、一定の電圧、電流です。略称で「DC」(Direct Current)と書きます。電子回路を動作させるために用意する電源(電気エネルギー源)は一般に直流です。
交流は、時間とともに変化する電圧、電流です。略称で「AC」(Alternating Current)と書きます。時間とともに変化するといっても、交流の場合は、時間とともに正負に変化します。たとえば、正弦波で変化する物は交流です。一方、時間とともに変化する物の、正の電圧だけ、例えば、5Vと10Vの間を行き来するような状態は「脈流」といって区別します(直流+交流)。おなじみ、コンセントの100Vは交流です。
さらに、周期的に正負が入れ替わる場合は、その周期、および逆数として周波数が定義されます。コンセントの100Vは、東日本では50Hz、西日本では60Hzです。
電子回路の主な要素と回路図
電子回路の主な要素
電子回路は様々な要素から成り立っています。「物」としてみた電子回路は、いうまでもなく、いろいろな部品が載っています。「機能」という目で見て、同種の部品をひとくくりにしたとしても、やはり多くの種類があります。その中の主要なものを挙げます。
- 電源:
電子回路が動くためには、電源がなければ話が始まりません。電源が回路が動作するための電圧をかけ、電流を流します。油圧や水圧のシステムで言えば、ポンプに相当するようなものです。
電源は、その出力の形態に応じて、分類されます。
- 電圧源: c.f. 電流源
普通、我々が「電源」といったら、(定)電圧源です。理想的な電圧源はその先についている回路にどれだけ電流が流れても(負荷抵抗が小さい)、一定の電圧を保ちます。よく、「○Vの電源」というのは、この電圧源です。
「理想的ではない、現実の」電圧源では、電流をどんどん流すと電圧が下がってきたり、保護が働いて止まったり、壊れたりします。が、とりあえずは、理想的な電圧源でこの先考えていきます。
- 電流源: c.f. 電圧源
普段はお目にかからないものに(定)電流源があります。希に電子部品で「○mA流しなさい」などと、電流で指定のあるものがあって、それに電流を供給する場合、また、コイルで発生する磁力や、モータのトルクなどの電流に比例する実験を行う場合につかいます。
- 直流電源: c.f. 交流電源
電源装置からは直流電圧/直流電流が発生します。一般的な電子回路を駆動するには、直流電源をつかいます。電池は直流電源です。
- 交流電源: c.f. 直流電源
交流電圧/電流が出てくる電源です。電化製品をつなぐコンセントは、おおざっぱに言えば、交流電源です(正確には、コンセントはただの接続端子であって、電源は交流発電機)。交流はトランスで簡単に電圧を変えられる(※)という利点があるため送電につかわれています。また、モータなどで交流電流で動作する物があります。「インバータエアコン」などの「インバータ」は一種の交流電源装置です。
※:電圧と電流の相互変換、減速機でトルクと回転速度を変換するような感じで、電圧×電流はほぼ変わらずに変換できる。
- 抵抗: (電気抵抗)
電子回路の主要な部品です。一般に電流の流れ具合を決めるのに使ったり、流れている電流を電圧に直すのに使います。詳しいことは次節、「オームの法則」で。
それと同時に、多くの電子部品を数学的に等価に考えたときに、この抵抗と見なして解析したり、あたかもそこに相当する抵抗があるかのように考えることがよくあります。
この、抵抗というものを理解すれば、アナログ回路はそれほどややこしいことはありません。
- コンデンサとコイル:
抵抗と並んで、回路上でよくみかけるのがコンデンサです。
コンデンサには電気(電子)をためる機能があります。詳しくはこのページの最後で扱いますが、「流れこむ電流を積分するとその電圧になる」という性質があるため、アナログ回路で積分器として使うことがあります。また、電源の線につないでおくと、電圧が変動しそうになったときに電流を出し入れしてそれを妨げてくれます(パソコンの中のコンデンサは95%以上がこの目的、一般的電子回路でも半分以上はこの目的)。
コイルは線をぐるぐる巻いた物です。この講義では使うことは多分ありませんが、電気エネルギーを磁気エネルギーとやりとりする性質があり、「電流を流しにくく、また減らしにくい」という性質があります。そのため、電流変化を抑える働きとして、電源装置などに使われます。
- 増幅素子:
入力された電圧、電流を、なんらかの特性に従って増幅して出力する部品です。
トランジスタ、オペアンプなどなどいろいろあります。たとえば小さな信号をオーディオアンプに入れるとスピーカーがガンガン鳴るのは、この増幅素子のおかげです。増幅無くしては、信号はどんどん減衰(弱まる)のみです。
ただし、しっかりと認識すべきは、増幅素子は大きくした電気信号を生み出す部品ではありません。増幅素子に同時につないだ電源装置から得た電圧、電流を、入力に応じて適宜しぼって出す部品です。蛇口をいくらまわしても、そこまで水が来ていなければなにも出てこないとのいっしょで、増幅素子には電源が必須です。忘れると、入力がほぼそのまま出てきたり、変な信号か出てきます。
回路図
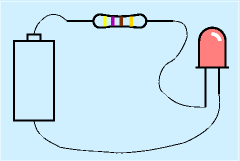 |
| 実体配線図 |
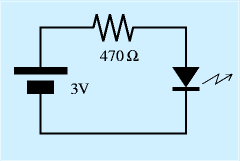 |
| 回路図 |
電子回路を書き表すために使う図が回路図です。
回路図では各部品を特定の記号に置き換えて記述し、それらを線でつないで配線とします。
一見すると、右図の「実体配線図」のような、部品の絵が直接書いてある方が直感的に分かりやすそうに思えますが、書くのは面倒ですし、部品が増えてくるとごちゃごちゃになりますし、人によって絵心のばらつきがでます。書くのが面倒な部品もあります。そのうえ、同じ機能、たとえば値の抵抗であっても、多くの種類があり、それらをとても書き分けられません。そこで、記号で書くわけです。
それが右図の「回路図」です。電池に相当する直流電源、抵抗、発光ダイオードを記号にしています。たとえば、実体配線図では電池を使っていますが、電源装置から電流を供給しても同じ図になります(なにを使うか明示するときは別途付記する)。
以下に、まずは覚えておいてほしい回路図の記号を示します。
| 対象 | 記号 | 説明 |
| 直流電圧源 | 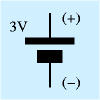 | すでに電池の記号として見覚えがあるかもしれませんが、この記号は直流電源全般を表します。電圧はそばに書いておきます。2個の長方形の細長い方が+(電位の高い方)を意味します(図中の+−記号は説明のためのもので、実際には不要)。なお、電池の記号にしたときに、この記号1個で1.5[V]という使い方を見たことがあるかもしれませんが、一般には1個で任意の電圧に使えます。 |
| 交流電圧源 | 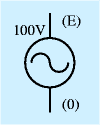 | 厳密には、直流も含めて、任意の電圧源です(直流は時間で一定という特殊なもの)。交流に正負が?と思うかも知れませんが、電源をたとえば正弦波などの関数で定義したときに、どちらを基準にするか、という問題があります。記号は対称なので、一般には下側の端子を基準に、上の端子が変化すると考えます(図中の0、E記号は説明のためのもので、実際には不要、この記号は横向きに書くことは稀です)。 |
| 固定抵抗 | 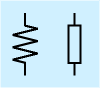 | 抵抗を表します。近年の規格では右の細長い長方形を使うように定められましたが、左のジグザグ記号がまだまだメジャーです。ジグザグは適当で良いわけではなく、端子の線に対称に、それぞれ山三つです。なお、可変抵抗、半固定抵抗と呼ばれる、値の変わる抵抗もあります。 |
| コンデンサ | 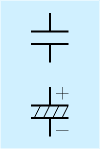 | コンデンサの記号は一番?その実体を表しています。コンデンサは2枚の電極を向かい合わせた構造です。コンデンサには多くの種類がありますが、その一群に電解コンデンサと呼ばれる、電極間に電解液が入っているものがあります。その間に電解液が入っているものは下図の斜線入りの記号を、そうでないものは上図の記号を使います。電解系のコンデンサは一般に極性があり、+─を明記します(逆接すると破裂したりする)。 |
| グランド、基準電位 | 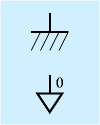 | 前述の電圧の基準点を示す記号です。この記号がつながった線が基準の電位になり、「この点の電圧は」などというときの基準になります。以前はT字に斜線の記号をよくつかっていましたが、最近は▽に0(電位0を示す)をつけた記号が多くなってきました。 |
| 配線接続 | 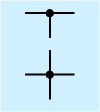 | 回路図では部品と部品は原則として縦横の線でつなぎます。ただ線が交差した場合には非接続、そこに黒丸がついている場合は接続を意味します。T字の場所は接続と断定できますが、その場合も省略せずに黒丸をつけます。 |
| 配線非接続 | 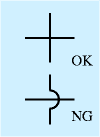 | 上述のように、黒丸がない線の交差は自動的に非接続になります。小学校では、下図のように線が飛び越えたような書き方を教えることもありますが、これをする必要はありません(そのかわり、黒丸を忘れたらアウト)。 |
この講義では上記のような記号を使っていきますが、回路図の書き方は(本来こまりますが)いくつかの流儀があります。基本的な思想は変わらないはず&一般には似た記号なので、たぶん、それらを見ても理解はできると思います。
また、「概念的」な回路(意味のみの回路)では、しばしば記号のみ書かれますが、実際に解析、設計したり、製作するための回路図は、必ず部品のわきにその値 and/or 部品番号がつきます(例:R1 470Ω)。
電子回路の基本法則 1:オームの法則
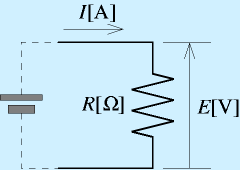
電子回路の一番の基本法則が「オームの法則」です。
電子回路のなかにある抵抗は、右図のように切り放して見ることができます。
左の方に図のように電源だけついているという場合はまれで、普通は左側にもいろいろな回路がつながっています。
が、ともかく、抵抗一本です。
この抵抗値R[Ω]の抵抗に、電流I[A]流れているとき、その抵抗の両端には
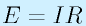
であらわされる電圧が生じます。電位で言えば、流れ込む側が流れ出す側より高くなります。
逆に、抵抗の両端に電圧Eがでていれば、その抵抗には
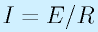
の電流が流れています。
抵抗に流れる電圧と電流は比例し、その比例定数が抵抗値であるともいえます。
純粋な抵抗においては、この法則はつねに成立しています。直流でも交流でもOKです。
また、説明を簡単にするために、抵抗一本だけを考えましたが、この抵抗の変わりに複数の抵抗などがまとめてつながっている場合も、同じように法則は成立します。その、直列つなぎ、並列つなぎについては、もうすこしあとで取り扱います。
このオームの法則とは関係ありませんが、このようなある部品に電流Iが流れ、電圧Eが生じている場合、
![P[W]=E[V]~I[A]](eqn/basicelec.bhtml.eqn3.gif)
で消費電力が表されます。
電子回路の基本法則 2:キルヒホッフの法則
キルヒホッフの第一法則
 3個以上の部品を接続するとき、その配線上には必ず接続点があります。実際に回路に電源を与えると、ある部品からはその点に電流が流れてきて、また別の部品にはその点から電流が流れ出していきます。
3個以上の部品を接続するとき、その配線上には必ず接続点があります。実際に回路に電源を与えると、ある部品からはその点に電流が流れてきて、また別の部品にはその点から電流が流れ出していきます。
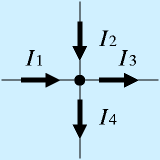
具体的に右図を見ます。4本の配線が一点で接続されています。この点に対して、左からI1、上からI2の電流が流れ込んできて、右にI3、下にI4の電流が流れ出しているとします。この場合には必ず、

という関係式が成り立ちます。言葉で言えば、「流れ込む電流の和と流れ出す電流の和は等しい」となります。
電流を水の流れにたとえて考えれば、当たり前と言えば、当たり前の話です。ですが、これがオームの法則と並んで、電子回路を考える上で基本となる法則です。
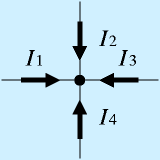 一般的には、ある点に対して、流れ込む方向を正として、電流を規定し、その総量がゼロ、すなわち
一般的には、ある点に対して、流れ込む方向を正として、電流を規定し、その総量がゼロ、すなわち
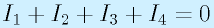
とも規定されます。
※「流れ出す方向を正」としても同じ。
どちらの表記にせよ、「正」の方向をきめ、逆向きに流れる場合は「負の電流」として考えることを覚えておいてください。これは直流の電流であっても、交流の電流であっても、つねに成立します。
キルヒホッフの第二法則
 第一法則が電流の法則であったのに対して、第二法則はどちらかというと電圧の法則です。
一言で言うと、「電圧は一周したら0」です。
第一法則が電流の法則であったのに対して、第二法則はどちらかというと電圧の法則です。
一言で言うと、「電圧は一周したら0」です。
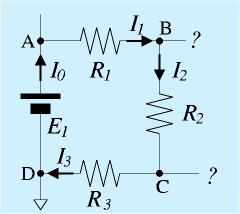
回路の一部に右図のような和になった部分があったとします。
回りになにもつながっていなければ、電流がどこかにいったり流れ込んだりしないので、I0〜I3は等しくなりますが、別の回路に配線がつながっている場合は、各配線の電流は一般に異なります。
ここで、接続点Dを基準として、各部の電圧を時計回りにたどって考えてみます。
まず、電源E1がつながっているので、A点の電圧(Dを基準とした電位)はE1です。
次に、抵抗R1について、オームの法則を適用します。電流I1が流れているので、B点を基準にしてA点の電圧は(抵抗R1にかかる電圧は)、I1R1になります。と、いうことは、D点を基準にすると、AでE1に上がって、そこから、I1R1下がるので、B点の電圧E1-I1R1になります。
同じように、R2も考えると、C点はD点を基準にE1-I1R1-I2R2になります。
さらに、R3も考えると、D点はD点を基準にE1-I1R1-I2R2-I3R3になります。
D点を基準に、D点をみたら、0になっていなければ変です。なので、この回路の場合
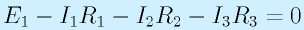
が成立していることになります。
※書いてはありますけど、ここではI0は無関係。
このように、回路のなかで輪になっている部分を取り出し、そこに挟まっている電源(もちろん、ないこともあります)と、抵抗に生じる電圧を考え、一周するとゼロになる、というのが第二法則です。
注意点は、電源がたどる向きと逆向きについていたら、負の電圧として、回る向きと逆向きに電流の正の方向を定義したら、抵抗で生じる電圧も逆にするということです。なので、回路を解析するときは、必ずどちらが正かを明確にきめておく必要があります。
さて、いまの話の中で、抵抗に電流が流れると、電圧が"-IR"と下がっていました。そのことから、抵抗の両端に電圧が生じることを「電圧降下」ということがよくあります。
表現としては「この抵抗の電圧降下(降下電圧)は○ボルトである」とつかうこともあります。
実例
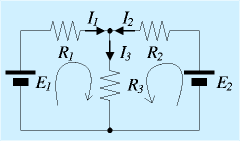 もう少し実践的?な例を上げます。この図では、電源が2個、抵抗が3個、途中で枝分かれしない線が3本です。
もう少し実践的?な例を上げます。この図では、電源が2個、抵抗が3個、途中で枝分かれしない線が3本です。
まず、キルヒホッフ第一の法則から、
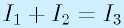
です。
次に、左側の輪に対して、時計回りに見ると、E1、R1にI1、R3にI3です。これに第二法則を適用して
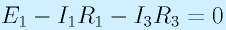
右の輪に対して、半時計回りに見ると、E2、R2にI2、R3にI3です。
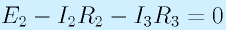
これらの式を整理してみます。
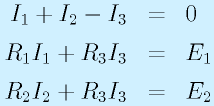
ここで、一般には、電圧は与え、抵抗はあらかじめきめてあるので、やってみなきゃわからないのは電流I1〜I3です。
未知の電流が3個、式は3本あるので、連立方程式を解けば、電流はもとまるはずです。
電子回路の動作を解析するときは、こういう計算を行います。
さて、この図にはもう一つ輪があります。一番外側です。E1, R1, R2, E2 という輪です。第二法則で式を立てると
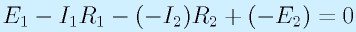 (逆向きを意識して書きました)
(逆向きを意識して書きました)
となります。
これと上の式との関係をみてみましょう。第2法則の式の1本目から2本目を引きます。
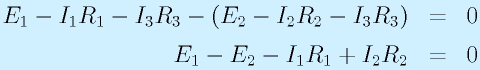
これは今外側の輪で求めた式と同一です。
よく、クイズで「この中にはいくつの三角形があるか?」なんて問題がありますが、このキルヒホッフの法則で式を立てる場合は複数の輪をつないだものは、わざわざ式を立てても他の式で表されるので、連立方程式を解くためには使えない、ということになってしまいます。そのため、それぞれ最小の輪で式を立てましょう。
(複数の輪にまたがる式を立てると、個々の輪で共用する線が必ず存在して、そこが打ち消し合う)
オームの法則、キルヒホッフの法則さえ忘れなければ、ややこしい回路図でも、案外気合いと根性で理解できます。
逆に、これら、特にオームの法則とキルヒホッフの第一法則を忘れると、この先この講義はとてもつらいものになりますので、しっかり覚えておきましょう。
抵抗の直列つなぎと並列つなぎ
コンデンサとコイル
抵抗と並んで重要な部品にコンデンサとコイルがあります。
おおざっぱに言って、コンデンサは「電気(電子、電気量)をためるもの」、コイルは「電流を維持するもの」です。
コイルについては、メカトロニクスには別の重要な側面があります。モータなどに使われる電磁石は、電気的にはこのコイルです(ふつうに、ものとしてもコイルと呼ばれますが)。そのため、電子部品としてコイルに触れることは少なくとも、なにか動くものを作ろうとすると、すぐにコイルに行き当たっています。
別の見方をすると、コンデンサ、コイルは電子回路に周波数特性をもたせる部品です。
抵抗は周波数によって特性は変わりませんが、コンデンサは高い周波数の電流ほど通りやすく、コイルは低い周波数の電流ほど通りやすいという特性があります。これをつかうと、特定の周波数の信号だけをとりだしたり、不要な雑音を取り除いたりできます。
身近な例ではラジオが挙げられます。いろいろな周波数の電波で放送が送られています。たとえば、NHK第2は1089kHz、東北放送は1260kHzなどです。この中から特定の局を選ぶという作業は、特定の周波数のみを受信するようにすることにほかなりません。以前からあるダイアルを回すタイプのラジオではコンデンサの容量を調整して、その選択を行っています。
ここでは、それら部品の特性を見てみます。
コンデンサ
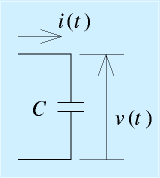 コンデンサの動作を数式で表すと、以下のようになります。
コンデンサの動作を数式で表すと、以下のようになります。
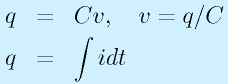
ここで、v(t)はコンデンサ両端の電圧、i(t)はコンデンサを流れる電流、q(t)はコンデンサにたまった電荷で、Cはコンデンサ大きさを表す数値「(静電)容量」です。
「電流を時間で積分すると電荷、電荷を容量で割ると電圧」という意味です。
つまり、電流を流し込んでいくと電圧が上がってきます。逆に、電流を抜く(i<0)すると、電荷が減り、電圧が下がってきます。
これが電気を蓄えるという意味です。
容量Cが大きいと、なかなか電圧が上がってきません。コップと洗面器に同じ流量で水を流し込むと、コップの方が先に水面があがってくるのと同じようなイメージです。
次に、周波数との関係を見てみましょう。周波数f[Hz]の正弦波電流
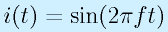
をコンデンサに流してみます。
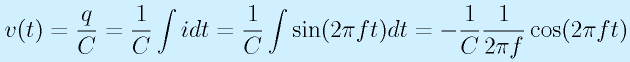
ここで、電圧、電流の振幅に着目します。電流は振幅1、電圧の振幅は(1/2πfC)です。
抵抗のときのオームの法則に当てはめて考えると、抵抗値に相当する値(インピーダンス)は「電圧/電流」で、(1/2πfC)になります。これは、「周波数fが高くなると抵抗が小さくなる」ということを意味します。
コイル
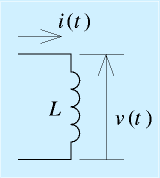 コンデンサと逆?の特性をもつのがコイルです。
コンデンサと逆?の特性をもつのがコイルです。
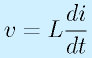
という特性を持ちます。ここでLはコイルの大きさを表すインダクタンスという数値です(一般に、インダクタンスが大きいと物としてのサイズも大きくなります)。この式の意味するところは、電流の時間変化に比例して電圧が発生するです。つまり一定の電流が流れている場合は電圧は発生しません(直流電源に直結してはいけません)。
周波数との関連を同じく見てみます。正弦波電流
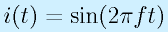
を流してみます。
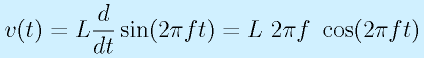
となります。電圧と電流の振幅を比べると、抵抗値に相当する値は 2πfL になります。
これは、「周波数が大きくなるほど抵抗が大きくなる」ことを意味し、すなわち電流が流れにくくなります。
同じように周波数依存性がある部品ですが、回路に周波数特性を与えるためにはもっぱらコンデンサが用いられます。これはコイルは電線を巻いた物で製造に手間がかかり、またサイズも大きいため、使いにくいためです。
ですが、メカトロ分野では「電流→力」の部品に良くつかわれます(スピーカもその一種)。
そのときは、このコイルとしての特性に注意する必要があります。電流が流れていないコイルをスイッチオンして電流を流そうとすると、その電流増加によって端子電圧が発生して、急には電流が増えません。逆に、急にスイッチオフする場合、スイッチなどでいきなり切り放すと電流が急速に減少します(流れる先がなくなるので強制的に減少)。その結果、端子にものすごい電圧が発生します。機械的なスイッチでもその高電圧による放電でダメージを受けることがありますが、半導体のスイッチの場合、その耐えられる限界を越えて壊れることがあり、注意が必要です。この高電圧を積極的に利用したのがエンジンの点火装置です。
また、自分ではコイルを作ったつもりがなくても、ただの配線でも多少のインダクタンスを持ちます。di/dtが大きい場合は問題になることがあります。
使うことは少なくとも、実は知っておかないといけないというのがコイルの特性です。
このページ、ここで終了
熊谷正朗
[→連絡]
東北学院大学
工学部
機械知能工学科
RDE
[| ]


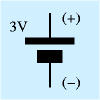






 電子回路の一番の基本法則が「オームの法則」です。
電子回路のなかにある抵抗は、右図のように切り放して見ることができます。
左の方に図のように電源だけついているという場合はまれで、普通は左側にもいろいろな回路がつながっています。
が、ともかく、抵抗一本です。
電子回路の一番の基本法則が「オームの法則」です。
電子回路のなかにある抵抗は、右図のように切り放して見ることができます。
左の方に図のように電源だけついているという場合はまれで、普通は左側にもいろいろな回路がつながっています。
が、ともかく、抵抗一本です。 3個以上の部品を接続するとき、その配線上には必ず接続点があります。実際に回路に電源を与えると、ある部品からはその点に電流が流れてきて、また別の部品にはその点から電流が流れ出していきます。
3個以上の部品を接続するとき、その配線上には必ず接続点があります。実際に回路に電源を与えると、ある部品からはその点に電流が流れてきて、また別の部品にはその点から電流が流れ出していきます。 一般的には、ある点に対して、流れ込む方向を正として、電流を規定し、その総量がゼロ、すなわち
一般的には、ある点に対して、流れ込む方向を正として、電流を規定し、その総量がゼロ、すなわち 第一法則が電流の法則であったのに対して、第二法則はどちらかというと電圧の法則です。
一言で言うと、「電圧は一周したら0」です。
第一法則が電流の法則であったのに対して、第二法則はどちらかというと電圧の法則です。
一言で言うと、「電圧は一周したら0」です。 もう少し実践的?な例を上げます。この図では、電源が2個、抵抗が3個、途中で枝分かれしない線が3本です。
もう少し実践的?な例を上げます。この図では、電源が2個、抵抗が3個、途中で枝分かれしない線が3本です。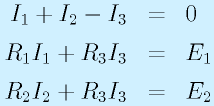
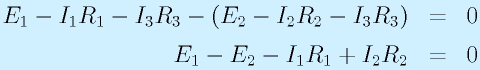
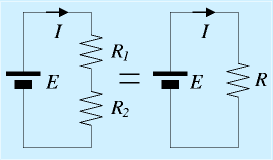 オームの法則、キルヒホッフの法則を使って、抵抗の合成を考えてみます。
オームの法則、キルヒホッフの法則を使って、抵抗の合成を考えてみます。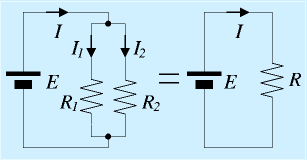 次に並列つなぎを考えます。抵抗R1,R2を並列につないだら、それぞれにI1,I2の電流が流れたとします。
まじめに輪ごとに考えてもいいのですが、この場合、R1,R2の両端の電圧は等しくEです。
次に並列つなぎを考えます。抵抗R1,R2を並列につないだら、それぞれにI1,I2の電流が流れたとします。
まじめに輪ごとに考えてもいいのですが、この場合、R1,R2の両端の電圧は等しくEです。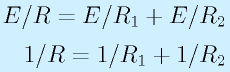
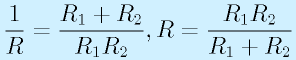
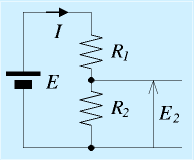 抵抗を直列つなぎしてつくる有用な回路に分圧回路があります。
抵抗を直列つなぎしてつくる有用な回路に分圧回路があります。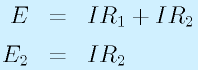
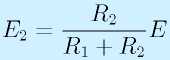
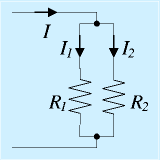 抵抗を並列にすると、電流の分岐ができます。
抵抗を並列にすると、電流の分岐ができます。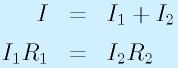
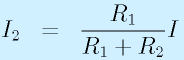
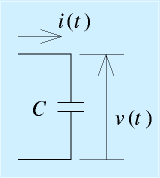 コンデンサの動作を数式で表すと、以下のようになります。
コンデンサの動作を数式で表すと、以下のようになります。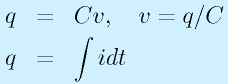
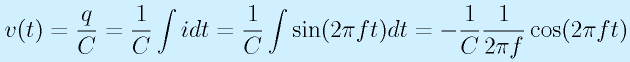
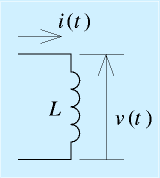 コンデンサと逆?の特性をもつのがコイルです。
コンデンサと逆?の特性をもつのがコイルです。