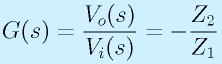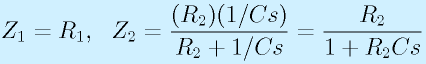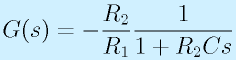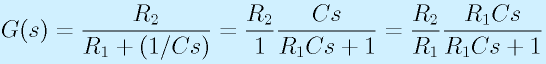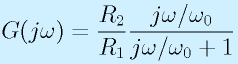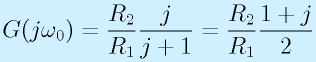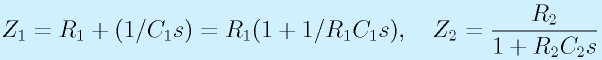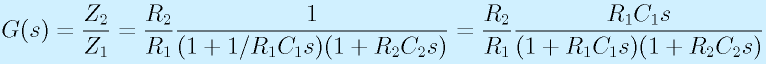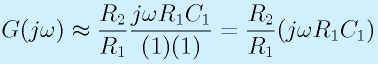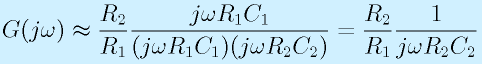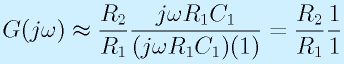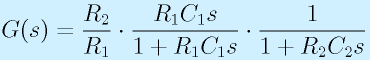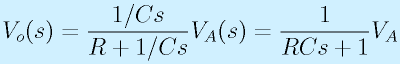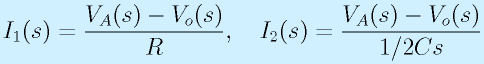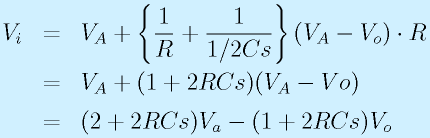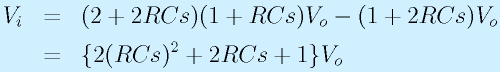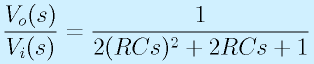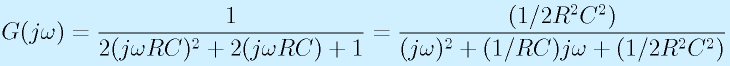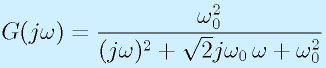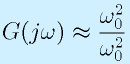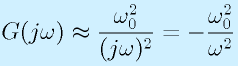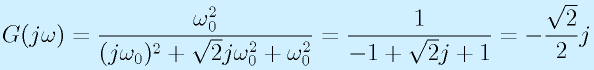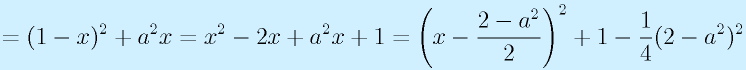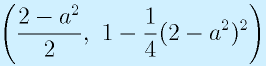ここでは、時間変化する信号を積極的に扱うための方法についてまとめます。
メカトロニクスIの領域でも時間変化する部分については、多少扱ってきました。
メカトロニクスIIでは、主にアクチュエータに電流を流したときのコイルの挙動、という意味で、時間変化が重要であると述べてきました。
しかし、本来、電気信号は様々な変化を伴っていることがふつうです。たとえば音声信号はマイクで空気の粗密=気圧の変化をそのまま電圧の変化になおしたものです。「変化していること」が大事な意味を持っています。
その点で、時間変化する信号と電子回路がどのような関係にあるかを知ることもまた、基礎中の基礎です。
電子回路の部品として、これまで抵抗、コンデンサ、コイルを見てきました。コンデンサ、コイルについては、微分、積分の関係で表されるように、「動きのある回路」は、回路を微分方程式で記述します。
微分方程式で記述した回路の挙動を考えるには、主に二つの方法があります。
一つは、数値計算の方法によって、微分方程式群に初期値を与え、そこからの時間変化を計算していきます。
この場合、全ての箇所の電圧、全ての経路の電流が、時々刻々とシミュレートされます。これは、回路シミュレータと呼ばれるソフトで行うことができ(Knoppix Eduにも搭載されています)、回路がちゃんと動くか、などの検証を行うためには適しています。もちろん、膨大な計算量であるため、コンピュータに計算してもらうことが前提です。
もう一つは、ある周波数での回路の動作を考える方法です。回路の入力として、正弦波を与えたとき、それがどのような波となって出てくるか、を考えます。
基本となる考え方として、「すべての波形はcos/sinに分解できる」という発想があります。これは、フーリエ級数、フーリエ解析を元にしています。任意の信号が入ってきたとしても、その信号を周波数成分ごとにばらしてしまって、その周波数毎に考えればよい、というわけです。
このためには、制御工学でも用いる、ラプラス変換やボード線図を道具として使うとあっさり解決します。
一般的な電気回路の教科書では、ラプラス変換を使わないで済ませるため、逆にわかりやすいとは思えない、難しい解説がなされています。が、「機械屋のための電子回路」の特権?として、制御工学のラプラス変換を借りてくることにしましょう。
電子回路と微分方程式
まず、回路を微分方程式で表すことを考えましょう。
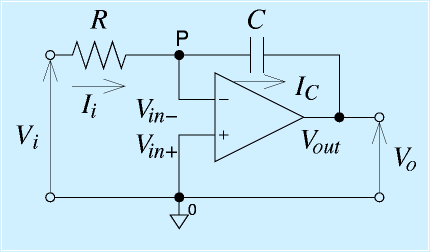 |
| 積分回路 |
右図の積分回路を例に考えます。図は、メカトロIのを持ってきたので大文字ですが、電圧、電流を小文字に読み替えて、特性を求めます。
まず、仮想接地により、P点の電圧は0、さらにオームの法則により、
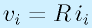
コンデンサは、その特性より
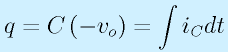
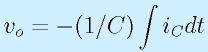
ii=iCなので、
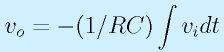
と求まります。
これは積分の形になっていますが、途中で、
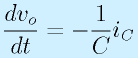
とすれば、全部微分方程式の形になります。
これに任意の波形、たとえば矩形波をいれたときどうなるか、といったことはある程度は手でも計算できますし、コンピュータで数値演算しても、求まります。
電子回路とラプラス変換
この回路をラプラス変換します。
ラプラス変換のお約束に従い、変換後の変数を大文字にします。
比例の式は、そのまま変換されます。
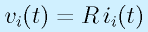 →
→
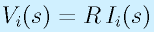
コンデンサが入った方の式は、積分、微分があるので、ラプラス変換の規則に従います。
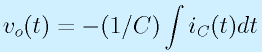 →
→
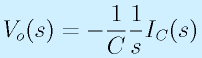 (積分は1/sになる)
(積分は1/sになる)
もしくは
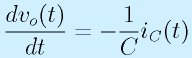 →
→
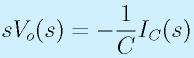 (微分はsになる。ただし初期値ゼロ)
(微分はsになる。ただし初期値ゼロ)
以上のように、ラプラス変換をすると、(制御工学でもそれを狙っていますが)微分積分が単なる「s」という文字になり、見た目がすっきりします。
このまま、式を解いてみましょう。ラプラス変換してもIi=ICなのは変わらないため、
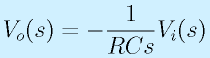
となります。これを逆変換すれば、
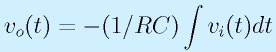
にはなります。
この計算法は、回路の規模によらず使える方法です。
回路の中にコンデンサやコイルが大量にあると、微分方程式としては大変な状態になりますが、ラプラス変換すれば「s」がいっぱい出てくるだけで済むため、見た目は平和になります。
インピーダンス
さて、回路として、ラプラス変換してみましたけど、より細かいレベル、部品単位でみてみましょう。
抵抗:
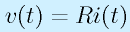 →
→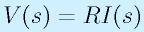
コンデンサ:
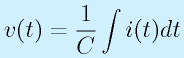 →
→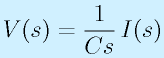
コイル:
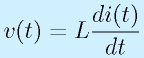 →
→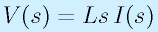
ここまで見ると、ラプラス変換後はすべて「V(s)=?I(s)」と抵抗におけるオームの法則と似た形になっていることがわかります。
つまり、抵抗については「?=R」のままですが、コンデンサは「?=1/(Cs)」、コイルは「?=Ls」です。
本来は「s」は微分積分を表すものでしたが、そのことを一度忘れてみると、VやIといった変化するはずのものに対する定数のように見えなくもありません。
先の例における、実際の回路の計算でも、そのように扱われています。
そこで、「1/Cs」や「Ls」をコンデンサやコイルの「抵抗値(のようなもの)だと思う」ことにします。
ただ、「s」のままでは実体があやふやなので、制御工学で周波数応答を考えたときのように、「s=jω」と考えます。
これは、角周波数ω(=2πf、f:周波数)の正弦波を入れることを想定します。
ここでいうjは虚数単位です(iではなくjの理由は、電子回路の世界では、iは電流で使われてしまっているから、です)
これにより、コンデンサ:「1/jωC」、コイル:「jωL」を角周波数ωにおける抵抗値と考えます。
もちろん、純粋な抵抗とは異なるため、この「交流に対応する抵抗」を「インピーダンス」と呼びます。文字はZで表します。
このインピーダンスの便利なところは、抵抗の並列つなぎ、直列つなぎの計算や分圧といった、抵抗にかかわる計算がそのまま成り立つことです。もちろん、インピーダンスは「複素数」なので、多少演算の手間は増えますが、微分積分を考えるよりは楽、また、回路における入力と出力の関係も、制御における「伝達関数」として出てくるため、増幅率はその大きさ、位相の進み遅れはその偏角として得られます。
以下では、時にはsのまま、時にはjωをつかって、回路の解析を行います。
ここでは、「インピーダンス」の計算を、フィルタ回路を例に見てみます。
フィルタ回路は、広い意味では「信号を目的にあわせて選別して通過、遮断する回路」ですが、ふつう、アナログ回路でフィルタといった場合は、信号を周波数で考えて、「ある周波数は通す(増幅する)けど、別の周波数は通さない(減衰させる)」回路のことを指します。
具体的には、「ある周波数よりも低い周波数の信号を通す」ローパスフィルタ、「ある周波数よりも高い周波数の信号を通す」ハイパスフィルタ、「ある範囲の周波数の信号を通す」バンドパスフィルタ(バンド=帯、周波数帯)、「ある範囲の周波数だけ通さない」バンドエリミネートフィルタ(バンドリジェクションフィルタ)などがあります。
フィルタとボード線図
フィルタ回路の特性を考えるとき、ほぼ確実に付随する物として、ボード線図があります。
ボード線図は、制御工学でもしばしば利用されますが、制御では他に選択肢があるのに対して、電子回路ではボード線図一本と言っていいほどです。
ボード線図は、回路の入出力の伝達特性(伝達関数)を、周波数に対する、増幅率と信号の進み遅れで記述した物です。
ただし、増幅率については、そのものではなく、log10をとって、20倍した値をゲインとしてつかいます。
信号の進み遅れについては、入力した正弦波の1周期を360度として、信号が進む場合を正、遅れる場合を負とする「位相」で考えます。
伝達関数をG(s)(G(jω))とすると、
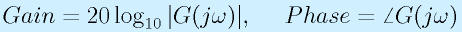
です。これらをそれぞれ、横軸を周波数の対数で書きます。
ちなみに、ゲインはその計算途中にあるlogのため、実質的に、ゲイン線図は両対数のグラフになります。両対数グラフは、
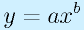
のグラフに対して、
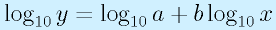
で表示するため、「何乗」(b)の関係にあるかがはっきりとわかるグラフです。また、縦軸が対数になっているため、ゲインG1の増幅回路とゲインG2の増幅回路を直列につないで、ゲインがG1*G2になったとき、単にグラフ上では縦方向の足し算になります。
これは位相についても同じで、45[deg]遅れ(-45[deg])と60度進み(60[deg])の回路をつなぐと、全体で15度進みとなりますが、これもグラフの上では上下方向に積むだけになります。
ボード線図は、本来回路の特性を直感的に見ることができるという利点がありますが、回路を直列につないだときには単に重ねていけばいいだけ、という特性も持っています。
ローパスフィルタのボード線図
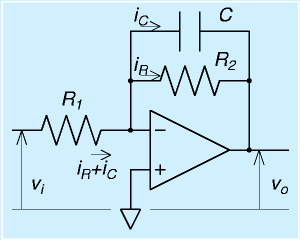 |
| 1次ローパスフィルタ回路 |
実際のローパスフィルタ回路を題材に解析してみます。
右図に示すように、反転増幅回路にコンデンサを1本追加した回路を考えます。
入力に、電圧vi(t)を与えたとき、出力に電圧vo(t)が現れます。
抵抗R2には電流iR(t)が、コンデンサには電流iC(t)が流れるとすれば、オペアンプ入力端子には電流が流れないため、キルヒホッフの法則より、抵抗R1には電流iR+iCが流れます。
以上をもとに、式を立てます。
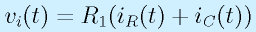
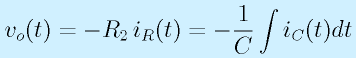
※オペアンプ−端子、仮想接地前提
これをラプラス変換します。
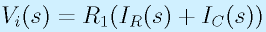
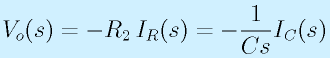
これを解きます。
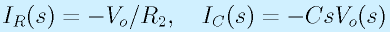
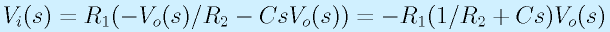
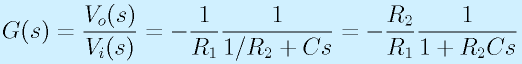
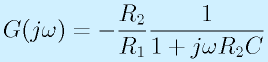
これをボード線図にすれば、このローパスフィルタの特性がわかります。
ボード線図にするため、s=jωとGの関係を調べてみましょう。
ただし、その前に「反転増幅回路」ゆえの「マイナス」は取っておきます。
- ω→0の場合:
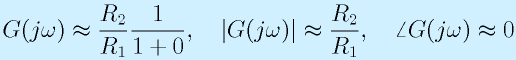
この場合、もとの反転増幅と同じ、R2/R1の増幅となります。
- ω→大の場合:
![G(j\omega)\approx\frac{R_2}{R_1}\frac{1}{j\omega R_2C},~~~|G(j\omega)|\approx\frac{R_2}{R_1}\frac{1}{\omega R_2C},~~~\angle G(j\omega)\approx\angle(\frac{1}{j})=-90\,[deg]](eqn/basicelec2.bhtml.eqn110.gif)
この場合、ωに反比例し、増幅率が落ちていきます。周波数が10倍になると、1/10になります。その漸近線が、反転増幅の線と交差する点は、ωが
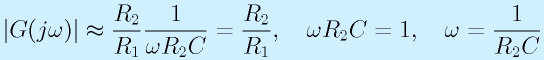
となるところです(ω=2πfより、f=1/2πR2C)。
また、位相=-90度ということは、90度の遅れになります。
- ω=1/R2Cの場合:
![G(j\omega)=\frac{R_2}{R_1}\frac{1}{1+j}=\frac{R_2}{R_1}\frac{1-j}{2},~~~|G(j\omega)|=\frac{R_2}{R_1}\frac{\sqrt2}{2},~~~\angle G(j\omega)=-45\,[deg]](eqn/basicelec2.bhtml.eqn112.gif)
このとき、もとの反転増幅の増幅率に対して、増幅率が√2/2(1/√2、約0.7倍)に落ちます。また、位相は-45[deg]になります。
以上をもとにすると、ある角周波数ω0=1/R2Cを境に、周波数が低い側はほぼ反転増幅回路として振る舞い、周波数が高い方は、周波数に反比例して増幅率が落ちていきます。両対数グラフで考えると、ω0を境に、周波数が低い側は水平の線、高い方は傾き−1の線に漸近します。この2本の線の交点は周波数ω0のところです。
位相については、ω0より低いところでは、遅れなし、高いところでは90[deg]遅れになっていきます。
継ぎ目である、ω0のところでは、増幅率が1/√2低下し、位相は45[deg]遅れになります。
| 角周波数 | ω<ω0 | ω=ω0 | ω>ω0 |
| ゲイン(相対) | 1 | 1/√2 | ωに反比例 |
| 位相 | 0[deg] | -45[deg] | -90[deg] |
この、継ぎ目は「ここからカットする」という意味で「カットオフ」と呼ばれます。
解析では、角周波数ωをつかうことが一般ですが、現実には周波数fで考えるため、f0=ω0/2π=1/2πR2Cをカットオフ周波数といいます。
一般に、その特性を出すのに関わったコンデンサ容量と抵抗値の積である「時定数」の逆数が深く関わります。
カットオフ周波数自体の定義は、「ゲインが-3[dB]落ちる周波数」です。-3[dB]は1/√2倍に相当します(20log10(1/√2)=-10log10(2)=-3[dB])。なお、この例では、漸近線の交点とカットオフ周波数が重なっていますが、回路構成によっては必ずしもそうとはなりません。
また、このフィルタは、ωの1乗に反比例することから「1次」のフィルタといいます(sが分母に1個、1階の微分方程式だから、などなど)。周波数が10倍で増幅率が10分の1になりますが、10分の1はゲイン表示では-20[dB]となります。そのため、この傾きを「-20[dB/dec](dec=decade=10)」と表すこともあります(別の世界では、-6[dB/oct], oct=オクターブということもある)。この減り具合をゲイン線図全体の特性を含めて「遮断特性」「減衰特性」ということもあります。
一般に、フィルタを設計するという場合は、フィルタの特性を選び、その回路に付随するカットオフ周波数の決定式を元に、回路の抵抗、コンデンサを決めていきます。実際には、コンデンサは選択の余地が少ないため、コンデンサを先に決めてから抵抗で調整します。(もちろん、大きすぎず、小さすぎずなども考慮)
また、「パス」だの「カット」だのいっても、ばさっと切り替わるわけではありません。あくまでなだらかに変化します。そのことを念頭に、あらかじめ、通したい信号と、遮断したい信号をなるべく周波数で分けておくことが重要です。
1次フィルタ
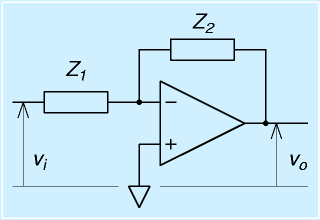 |
| 1次フィルタ回路 |
より、汎用的な回路を考えます。
一見、反転増幅回路ですが、抵抗の変わりに、Z1, Z2 と記載された素子がつながっています。
これは、以下で、抵抗やコンデンサをはめていくための部分で、インピーダンスがそれぞれZ1, Z2です。
この回路の伝達関数は、
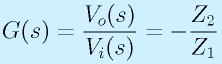
となります。基本的には、反転増幅回路の考え方と同じで、Z1とZ2を流れる電流が同じとすれば、
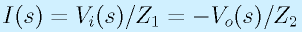
です。
先ほどの、ローパスフィルタの例はZ1=R1, Z2=R2とCの並列つなぎです。そのため、
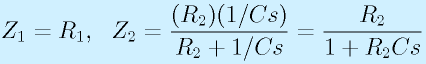
となり、
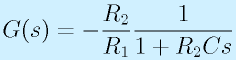
となります。(最初からこうすれば早いものの、基本のため、上ではは手間をかけた)
先ほど、同様、マイナスはとりあえず置いておいて、Z1,Z2の組み合わせをみてみましょう。
- Z1,Z2が抵抗:(反転)増幅回路
- Z1が抵抗、Z2が抵抗とコンデンサの並列:ローパスフィルタ
- Z1が抵抗R1とCの直列つなぎ、Z2が抵抗R2の場合:
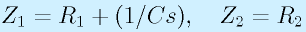
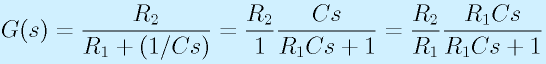
さらに、jωを入れて、ω0=1/R_1Cとすると、
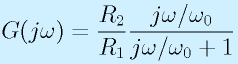
となります。ローパスフィルタのときと同じように考えると(R2/R1を省く)、
| 角周波数 | ω<ω0 | ω=ω0 | ω>ω0 |
| ゲイン(相対) | ωに比例 | 1/√2 | 1 |
| 位相 | 90[deg] | 45[deg] | 0[deg] |
となります。
※ω=ω0で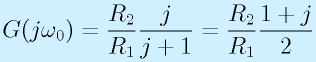
これは、ω0よりも高い周波数で信号を通し、ω0より低い周波数を減衰させる、ハイパスフィルタになっています。
その傾きは、ωに比例し、20[dB/dec]で、カットオフ周波数はf0=1/2πR_1Cです(ローパスと抵抗が違うことに注意)。また、位相は最大で90[deg]進みます。
- Z1が抵抗R1とC1の直列つなぎ、Z2が抵抗R2とコンデンサC2の並列つなぎの場合:
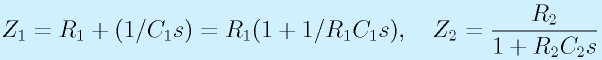
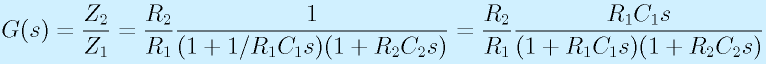
となります。ここで、R1C1>R2C2とします。
まず、ω→0のとき、
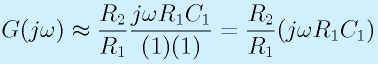
となります。これはハイパスフィルタと同じような特性を持っています(ωに比例、90度進み、カットオフ1/R1C1)。
つぎに、ω→大のとき、
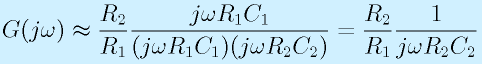
これは、ローパスフィルタと同じような特性を持っています(ωに反比例、90度遅れ、カットオフ1/R2C2)。
最後に、(1/R1C1)<ω<(1/R2C2)で、少し乱暴に無視すると、
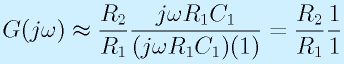
となり、ただの増幅になります。
ωが(1/R1C1)より小さいところと、(1/R2C2)より大きいところを減衰させ、その間を通すことから、これはバンドパスフィルタになります。ただ、重なる部分の幅の大きさによって、増幅率が平らになるところができたりできなかったりします。
※ふつうは、R1C1<R2C2にわざわざしない<ピークでもかなり減衰してしまうため。
さて、最後のバンドパスフィルタの式をよく見ると、
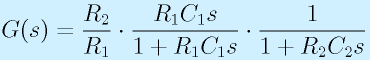
となっています。これは、反転増幅の部分、ハイパスフィルタ・ローパスフィルタの特性の本体(増幅以外の部分)を乗じた物です。
つまり、バンドパス=ローパス+ハイパス、と、回路の形からも想像できる性質を持っています。
というところに、実験データから気づいて欲しいのが、機械工学実験I、「電子回路の基礎」のデータです。
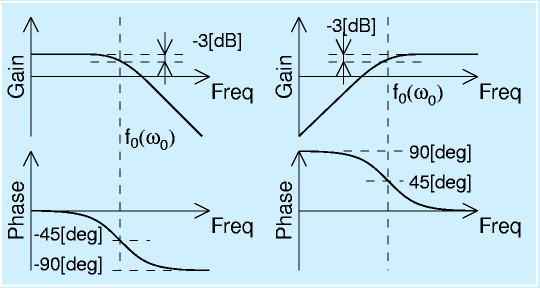 |
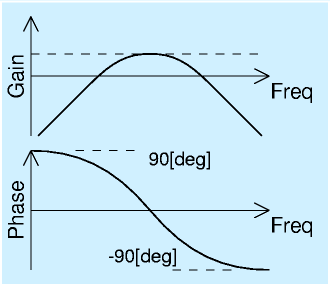 |
| ローパスフィルタ、ハイパスフィルタ ボード線図 |
バンドパスフィルタ ボード線図 |
2次フィルタ
先ほどの1次フィルタは周波数に比例もしくは反比例する遮断特性でしたが、より急峻な特性のフィルタが必要なことがあります。
そのためには「高次フィルタ」と呼ばれる回路がつかわれます。ここでは2次フィルタの一例を見てみます。
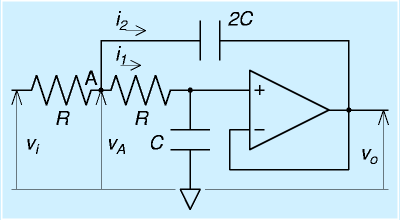 |
| 2次フィルタ回路 |
この回路は、抵抗値Rの抵抗が2本、容量Cのコンデンサ、容量2Cのコンデンサからなります。
図の電圧、電流について、インピーダンス(ただし、jω=sのまま)を用いて回路を検討します。
まず、オペアンプはボルテージフォロワを構成しているため、増幅率は1です。そのため、
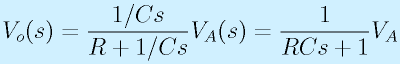
2カ所の電流は、
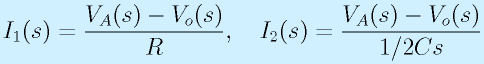
となります。また、Vi,VAの関係は、
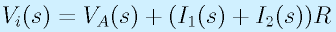
です。
ここから、VA,I1,I2を消去します。まず、I1、I2を代入して、
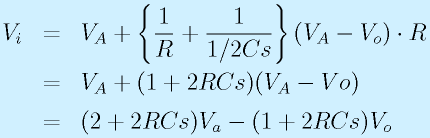
ここからVAを消去します。
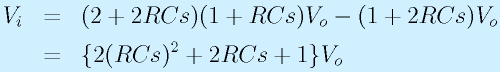
伝達関数は、
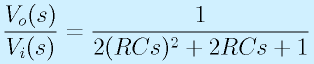
となります。
この特性を調べます。
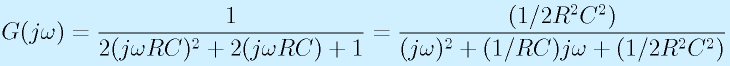
ここで、1/(√2RC)=ω0とおくと
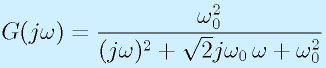
となります。
例によって、ωの大きさで考えます。
- ω<<ω0の場合:
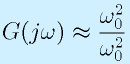
となるため、
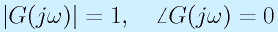
となります。
- ω>>ω0の場合:
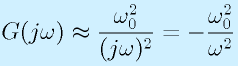
となるため、
![|G(j\omega)|=(\omega_0/\omega)^2,~~~\angle G(j\omega)=-180[deg]](eqn/basicelec2.bhtml.eqn212.gif)
このとき、ωの2乗に反比例して(1/ωの2乗に比例して)減衰します。言い換えれば、周波数が10倍になると、信号は100分の1になります。
なお、厳密には、「−」が-180[deg]なのか+180[deg]なのか(または別の角度なのか)はこれだけではわかりませんが、次の計算も合わせると、-180[deg]であることがわかります。
- ω=ω0の場合:
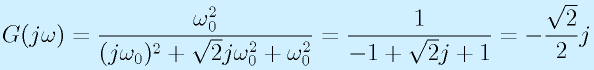
つまり、
![|G(j\omega)|=\sqrt{2}/2,~~~\angle G(j\omega)=-90[deg]](eqn/basicelec2.bhtml.eqn214.gif)
となります。これは-3dBとなっているため、このω0がカットオフ角周波数であることがわかります。また、そのとき90度遅れることもわかります。
1次のフィルタに比べ大きく減衰するようになります。これでも足りないとき、3,4,5次のフィルタを使います(回路的には、2次と1次を組み合わせて直列接続します)。
2次フィルタは、抵抗、コンデンサの値によって、様々な特性を持たせることができます。値によっては共振のような特性も表れます。
ここで例に挙げた2次フィルタは、通過域(ω0より低周波)において、増幅率が1を超えないぎりぎりのフィルタでバタワース特性と呼ばれます。
カットオフ周波数近辺で、これよりなまったフィルタを作ることもできますが、ありがたみはあまりありません。これより急峻になるフィルタを作ると、通過域の上端あたりに増幅率が1を超える共振的な部分が出てしまいます。
計測信号を扱う場合は、変に増えても困るため、このバタワースがよく使われます(コンデンサの値も1:2と手頃)。
そのほか、ハイパスフィルタやバンドパスも2次があります。また、バタワースの他、チェビシェフ特性という、通過域に山ができることを覚悟の上で使う、カットオフ近辺が急峻な設計もあります。
※補遺:ゲインが1を超える囲えないかの確認:
分母の√2を変数aとおいて、ω0=1として(ω0に関係ないため)、分母の大きさの2乗を計算する:
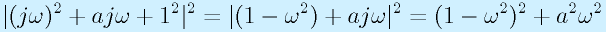
ω2をx(≧0)とおいて、最小値を検討する。
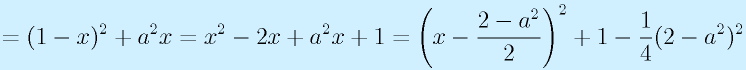
これは、頂点が
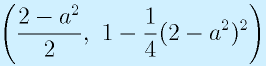
の放物線である。
x≧0であるため、もし、頂点がx≦0にあれば、つまりa≧√2であれば、最小値はx=0(ω=0)における1となる。
分母が1以下であれば、|G|は1を超えない。
もし、頂点がx>0に出てくるなら、つまりa<√2であればこの頂点の値が最小値となるが、これは1未満となる。そのため、|G|が1を超えるところが出てくる。
なお、a=0の場合、「大きさ」はω=1において、0となるため、振幅無限大となる。もちろん、現実的にはあり得ないが、共振特性の鋭い回路を作れる可能性を示唆している(が、部品誤差などにより面倒。一般に共振させる場合はLCによる回路を使う)。
本節のまとめ
ここでは、ラプラス変換の助けを借りることで、本来は微分方程式で表される、コンデンサなどを含む回路を解析しました。
また、その過程で、インピーダンスと呼ばれる、交流で見た抵抗値を導入しました。
フィルタは設計することは、「虎の巻」を元に部品定数を計算すれば、それなりに簡単にできますが、アナログ回路として実用にすることは案外大変です。組み立てることはできても、精度が出ない場合もよくあります(特に、コンデンサのせい)。
あくまで、「通す信号」と「落とす信号」をはっきり区分けできるようにしておいて、その間をフィルタでカットする、という使い方が一般です。

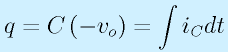
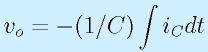
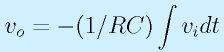
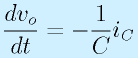
![]() →
→
![]()
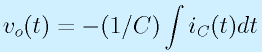 →
→
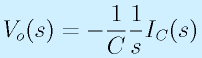 (積分は1/sになる)
(積分は1/sになる)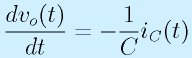 →
→
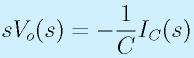 (微分はsになる。ただし初期値ゼロ)
(微分はsになる。ただし初期値ゼロ)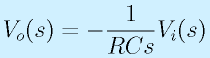
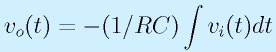
![]() →
→![]()
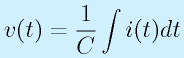 →
→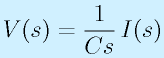
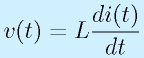 →
→![]()

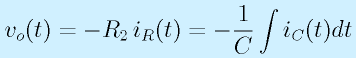
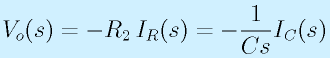
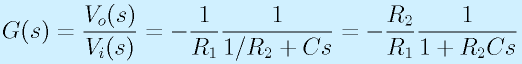
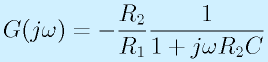
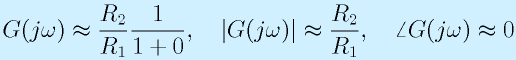
![G(j\omega)\approx\frac{R_2}{R_1}\frac{1}{j\omega R_2C},~~~|G(j\omega)|\approx\frac{R_2}{R_1}\frac{1}{\omega R_2C},~~~\angle G(j\omega)\approx\angle(\frac{1}{j})=-90\,[deg]](eqn/basicelec2.bhtml.eqn110.gif)
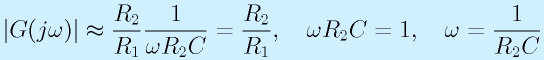
![G(j\omega)=\frac{R_2}{R_1}\frac{1}{1+j}=\frac{R_2}{R_1}\frac{1-j}{2},~~~|G(j\omega)|=\frac{R_2}{R_1}\frac{\sqrt2}{2},~~~\angle G(j\omega)=-45\,[deg]](eqn/basicelec2.bhtml.eqn112.gif)