ディジタル回路の基礎

最終更新： 2012/01/11 10:22:21 ［｜　］　 最終更新： 2012/01/11 10:22:21

ディジタル回路

前ふり

ディジタルというと思い浮かべるものはなんでしょうか。

よく、アナログとディジタルは比較されます。 だいたい、これまでは身の回りで「ディジタル」と名前につくものは、数字、しかも「日」な数字が表示される物と相場が決まっていましたが、最近はもうすこし本来のディジタルの意味が見えるようになってきて、DVDの一個がディジタルだというのも知られていると思います。
（DVD=Digital Versatile Disk , versatile=多芸、Digital Video Disk ではありません＜多分最初はそういう発想だったんじゃないかと）
昔は、音を記録するのも映像を記録するのもアナログでしたが、いまどきはディジタルです。音声や映像信号そのものはいまでもアナログなことが多いのですが、徐々に再生に関しては完全にディジタル処理だけというシステムが出始めています。
では、なぜ、ディジタルがどんどん増えてきているのでしょう。アナログに対して優位性があるからとは思えます。

以下、思い当たる比較をします。
比較対象アナログディジタル
値の扱い電圧や電流の連続的な大小をそのまま信号の値として考える。電圧や電流をオン／オフ、十分大きい／十分小さいと極端に違う状態でつかい、信号は２種類しか考えない。値の種類を多くする場合は信号線を複数本にする。
信号の扱いやすさ線一本で値が伝わるため、配線は少ない。しかし、途中の部品の精度、信号へのノイズなどの影響を直接受け、精度の低下要因がいろいろある。値の種類に応じて、線が多くなる。たとえば、０〜５万程度の整数値を扱う場合は最低１６本必要。しかし、信号の電圧が極端であるため、多少の回路の誤差の影響は受けず、またノイズなどの影響も受けにくい。そのため、値の精度は原則として低下しない。
回路の作りやすさ配線本数はすくない。しかし、設計や作り手の腕で回路の性能が変わる。配線本数は非常に多くなりやすい。しかし、普通は正しく配線すれば「だれがつくっても動く」回路ができる。

※ディジタルでも、３種類以上の値を持たせる多値論理というものもあります。たとえば、パソコンのネットワークの線、＋１、０、−１相当の３値です。

※ディジタルで、線一本で、時間方向に送る信号を高速で切り替えて、線一本で多くの情報をおくる「シリアル」という方式があります。線をたくさん使う方法は「パラレル」。パソコンでは、通信端子の多くはシリアル方式、プリンタ接続用のコネクタ、内部に増設するボード、ハードディスク、メモリなどはパラレル（最近シリアル化が進みつつある）。

ディジタル回路は配線こそ多くなりますが、なれれば単純な物で、失敗もしにくいため、それほど難しくありません。また、いまどきは電気製品でコンピュータを積まない物は少なくなってきていますが、コンピュータはディジタル回路の固まりです。そんなわけで、ここではディジタル回路について学びます。

ちなみに、針が回る時計、よく見ると、秒針は１秒ごとか、４分の１秒ごととかで進んでいます。あれ、アナログ時計と称しますけど、中は普通はディジタル回路でできています。

なお、Digital の表記として、よく使われるのは「デジタル」ですが、専門的には普通な原音に近い「ディジタル」をここでは使用します。

ブール代数と２進数

ブール代数

ディジタル回路は線一本について、オンかオフか、電圧が高いか低いか、といった２種類の値のみをつかいます。 この値をこれから１と０で表します。ちなみに、オン＝１とは決まっていません。どちらが１でどちらが０かは、回路を設計するときに、最初に決めます。
なお、ディジタル回路を構成するディジタルＩＣの特性は、電圧の高低である、ＨとＬで表します。

この１と０を取り扱うとき、ブール代数というものを使います。日常的に数学では四則演算が定義され、それに基づいて様々な演算が行われますが、ブール代数は「０と１しかない」ことを前提とした数学です。逆に、このブール代数（論理数学）を満たすようにディジタル回路の構成要素が組み立てられるため、「ロジック回路」と呼ばれることもあります。
この数学は「０と１」しかないのですごく簡単です。以下、見てみましょう。


基本演算の定義

四則演算に加減乗除があるように、ブール代数にも基本となる演算があります。 ともに成立すると成立する「かつ」にあたる論理積AND、一方が成立すれば成立となる「もしくは」にあたる論理和OR、成立と不成立をひっくりかえず「ではない」にあたるNOTが基本になります。

それぞれ、以下のように定義されています。
ABA AND BA OR BNOT A
00001
01011
10010
11110

これだけです。逆に、この理論が成り立つように回路を設計して動かすと、ディジタル回路になります。
さて、いちいちANDとかORとか書いているとうっとうしくなるので、普通は数式で書きます。

一見すると、普通の数学と似ているのですが、意味合いは異なるので注意が必要です。

これらについて、基本法則があります。

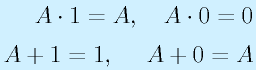交換則、結合則、分配則の前半までは、普通の数学も一緒ですが、そこからが、異なってきます。 吸収則はよく考えてみるとわかります。上の定義で、B=0, B=1とおいてみれば一目瞭然です。
分配則の後半について、試しに証明してみます。
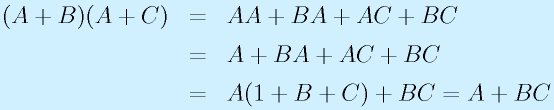
(A+B)(A+C)&=&AA+BA+AC+BC\nonumber\\&=&A+BA+AC+BC\nonumber\\&=&A(1+B+C)+BC=A+BC
となります。

これに加えて、非常に大事な法則、「ド・モルガンの法則」があります。
\overline{AB}=\overline{A}+\overline{B},~~~\overline{A+B}=\overline{A}\cdot\overline{B}
これは「ＡＢの否定は、Ａの否定もしくはＢの否定」とかけますが、ANDとORとNOTがあったときに、回路設計やプログラム開発において互いにいれかえることができます。
たとえば、日常的な例では
「明日は晴れて暖かくなる」
の否定は、
「明日は晴れないか、暖かくない」
になります。別のたとえをすれば、
「材力の単位をとれなかった」もしくは「熱力の単位をとれなかった」
は
「材力と熱力、両方の単位がとれた」
の否定になります。

これをブール代数的に証明するのは簡単です。
AB/A/B/(AB)/A + /B/(A+B)(/A)(/B)
00111111
01101100
10011100
11000000

回路の規模が小さく、手計算できるなら、このような表「真理値表」を作成すると、簡単に証明できます。

これら法則は、ディジタル回路を読み書き設計するときに大変重要なものなので、覚えておくようにしましょう。

２進数

ディジタル回路では、線一本で２つの状態しか表せないため、場合の数が多いとき、また数値を表すときには、そのままでは使えません。そこで、線を束にして使います。たとえば、線を４本用意すると２×２×２×２＝１６通りの状態を表すことができます。

これを数値として使う場合には、２進数をつかいます。
b3,b2,b1,b0正数のみ正負１６進数
０００００００
０００１１１１
００１０２２２
００１１３３３
０１００４４４
０１０１５５５
０１１０６６６
０１１１７７７
１０００８−８８
１００１９−７９
１０１０１０−６Ａ
１０１１１１−５Ｂ
１１００１２−４Ｃ
１１０１１３−３Ｄ
１１１０１４−２Ｅ
１１１１１５−１Ｆ
４本の線にb0〜b3と名前をつけます。b0が下位、b3が上位にあたります。それぞれを「ビット」と称することが一般的です。

これで正の正数のみを表す場合は、０〜１５を表のように割り当てます。 b0〜b3部分はよくみると、普段１０進数で数えるときに０→９まで数えると桁上がりするように、０、１ときたらもう桁上がりするというだけで、特に変なルールはありません。単に順番にならんでいるだけです。
別の見方をすると、
b_3\times2^3+b_2\times2^2+b_1\times2^1+b_0\times2^0
で計算されるとも言えます。 負の数も使いたいときは、０〜７までは同じで、８〜１５の部分は正数のときから「１６」引きます。別の見方をすると、２進数で最上位のb3が、「負」を表す値になって、ここが「１」のときに、b2〜b0の数値から８を引くようになっています。こう表記すると便利な理由はあとで説明します。

最後の１６進数というのは、プログラムをつくったりするときに扱いやすくするための数字です。見ての通り、２進数と１０進数は桁が多くなってくると直感的には変換できません。一方で、数値を２進数で表記するとなると（機械をいじるソフトをかくとそういうことがあります）、０と１をひたすら羅列するとほぼ間違いなく、数え間違いなどのトラブルがおきます。そこで、２進数と直接変換でき、ある程度人間が見てもわかりやすいものとして１６進数が使われています。具体的には、２進数を４桁ごとに区切り、０〜９、Ａ〜Ｆの１６の数と置き換えます。四則演算は頭のなかでやるには困難を極めますが（９９ならぬＦＦ？）、表記という点では１０進数よりもディジタルよりです。

さて、次に、２進数の演算です。

これでおしまいです。１０進数に比べてはるかにルールは簡単ですがその分、桁数は多くなります。
  • 足し算例（５＋１３）：
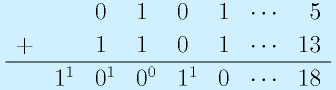
    \begin{array}{clllllcr}&&0&1&0&1&\cdots&5\\+&&1&1&0&1&\cdots&13\\\hline &1^1&0^1&0^0&1^1&0&\cdots&18\end{array}
    １０進数にくらべて繰上がりが多発します。

    掛け算例（３×５）：
    \begin{array}{rrrrrrrrr}&&&0&0&1&1&\cdots&3\\&\multicolumn{2}{r}{\times}&0&1&0&1&\cdots&5\\\hline &&&0&0&1&1\\&&0&0&0&0\\&0&0&1&1\\0&0&0&0\\\hline 0&0&0&1&1&1&1&\cdots&15\end{array}
    基本的に、１を乗じなければ０になるので、積の２行目４行目はなくてもかまいません。また、乗算回路は加算回路（と０と差し換える回路）を並べただけで作れます。

  • 正負の数の演算
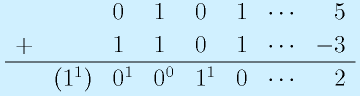
    \begin{array}{clllllcr}&&0&1&0&1&\cdots&5\\+&&1&1&0&1&\cdots&-3\\\hline &(1^1)&0^1&0^0&1^1&0&\cdots&2\end{array}
    一般に、４桁の数値で加算するという回路を組むと、４桁よりはみ出した部分は無視されます（ので、先ほどの足し算の例は、５桁以上用意しておかないといけない）。これと、先ほどの負数の定義を使用すると、こういう計算になります。逆に、負の数でも問題なく足し算できるように作られたのが、この負数の定義なわけです。
  • ×（−１）
    減算＝「×（−１）」して加算なので、正負反転があれば減算できます。
    負にするには、各ビットをNOTして、全体に１を加えます。
    例：５
    ５＝０１０１→NOT→１０１０→(+1)→１０１１→−５
    ちなみに、この１を加えるために、減算回路は加算回路が２個必要になりそうですが、加えるのは１だけなので、最下位にも桁上がりの演算を入れておいて、これを加えます。詳しくはいずれ。
    以上が２進数の概要です。１０進数でも除算はやっかいですが、２進数でもやっかいですので略しますが、乗算が×０×１しかないため、商の数字を確定していく作業は単純に大小比較だけですみます。

    ディジタルＩＣの基礎

    ディジタルＩＣ

    ディジタルＩＣは、ディジタル回路を作るために使用するＩＣの総称です。その種類は無数にあり、ＣＰＵなどもディジタルＩＣの一種です。 その中でも、ここではごく小規模で汎用のものを扱います。

    ディジタル回路では、上述のように、電圧信号をはっきり区別して使用します。ディジタルＩＣは、そのような特性、すなわち、入力電圧については、どこかに境界をもうけて、その上下で入力が０にあたるか１にあたるかを決定します。また、出力は、なるべく両極端の電圧が出るようにします。
    たとえば、
    出力０≒０　　　　　　　　　　≒VCC(電源電圧)出力１
    入力０扱い０〜1/2 VCC1/2 VCC〜VCC入力１扱い

    のように、出力は０Ｖかその電源電圧近辺かのどちらかを出力し、入力では半分より大きいか小さいかで判断します。

    ブール代数では、０か１かで表しましたが、ディジタルＩＣでは、物理的に電圧が低いか高いかでその値が扱われます。 そのため、ディジタルＩＣそのものの特性を表すために、電圧が低い状態をＬ、電圧が高い状態をＨと表示した真理値表も良く用いられます。以下では、混乱を避けるために、一般的な対応関係であるＬ＝０、Ｈ＝１でそのまま表記します。 ただし、ものによっては逆にＬで１を、Ｈで０を表すことがありますので注意は必要です。

    汎用に使えるディジタルＩＣはいくつかのシリーズがあります。その中の代表的なものを以下にあげます。

    これらのシリーズは、それぞれ１００〜数百種類といったＩＣで構成され、その機能、足配置などをまとめるとそれだけ本が一冊できるくらいですが、普段使うものはわりと決まっていますし、回路を構想する段階で「手抜きをするため」多少複雑なＩＣを探してくることが一般的です。ディジタル回路は上述のブール代数にそうとうするものだけで構成されるため、気合いと根性さえあれば、３種類だけで作り上げることができますが、それだと大変なのである程度あらかじめ機能をまとめたものが存在するわけです。

    ロジックゲート

    汎用ディジタルＩＣは非常に多品種ですが、よくつかわれる、基礎となるものがいくつかあります。 それらは、ブール代数の基本の三要素やそれに準じる単純なもので、ゲートと呼ばれています。 以下に、それらの名称、記号、機能(真理値表)を示します。

    基本要素
    名称 ANDゲート ORゲート インバータ
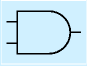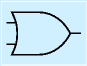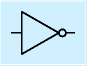    記号 ANDゲート ORゲート インバータ
    論理式
    AB A AND B A OR B NOT A
    00 001
    01 011
    10 010
    11 110

    準基本要素
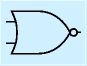
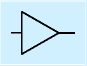
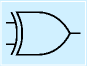
    名称 NANDゲート NORゲート バッファ XORゲート
    記号 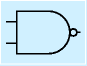NANDゲート NORゲート バッファ XORゲート
    論理式
    AB A NAND B A NOR B A A XOR B
    00 1100
    01 1001
    10 1011
    11 0010

    多入力ゲート NAND(なんど)：NOT AND の短縮。
    NOR(のあ)：NOT OR の短縮
    バッファ：信号増強 (内部はNOT NOTが多い)
    XOR(EX-OR、えくすおあ)：Exclusive OR、排他的論理和＝HHのときにはLになるOR。

    これらが、ディジタル回路での基本的な要素になります。

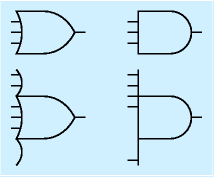
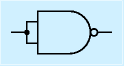
    AND, OR (NAND, NOR)に関しては、３以上の多入力のものがあり、それらは単に入力の本数を増やして右図のように表現します。

    最強のゲート、NAND

    NANDでNOT ブール代数のところでは、AND, OR, NOT ですべてが表現できるといい、上では、AND, OR, NOTに加えて、NAND, NOR, NOT, XORのゲートを追加しました。実は、この中で、NAND(NOR, XORもですが)だけがあれば、すべてがつくれます。

    まず、NANDの真理値表をあらためて。
    ABA NAND B
    001
    011
    101
    110

    ※ A=H, B=H のときのみ Lになると頭に入れると早い。
    ここで、入力を右図のように束ねます。すると、真理値表は、
    ABA NAND B
    001
    110

    のみとなり、これは NOT A と同じになります。

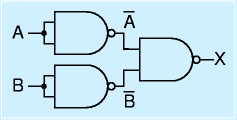    NANDでOR 次に右図のように NANDゲート三個をつなぎます。左２個はいまのNOT相当です。
    真理値表を書くと、
    AB/A/B(/A AND /B)/A NAND /BA OR B
    0011100
    0110011
    1001011
    1100011

    となり、ORと等価になります。これは、論理式で書いても確認できます、
    \mbox{NOT} ( \overline{A}\cdot\overline{B} )=NOT ( \overline{A+B} ) =A+B
    （１回目の等号はド・モルガン）

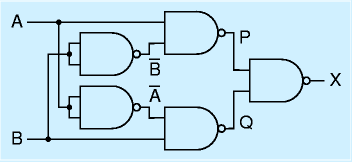    NANDでXOR 最後にXORをつくってみます。まずは天下り式に右図。
    AB/A/BPQP NAND QA XOR B
    00111100
    01101011
    10010111
    11001100

    ※ P= NOT(A・/B), Q= NOT(/A・B)
    また、XORの定義から、論理演算でも求められます。出力を"H"になる入力のORでつくります。
    X&=&A\overline{B}+\overline{A}B=\overline{\overline{(A\overline{B})}\cdot\overline{(\overline{A}B)}}
    あとは、先ほどのORを活用する形で、回路にすると右図になります。
    そのほかにも
    X&=&A\overline{B}+\overline{A}B=A\overline{B}+A\overline{A}+\overline{A}B+\overline{B}B\nonumber\\&=&A(\overline{A}+\overline{B})+B(\overline{A}+\overline{B})=(A+B)(\overline{A}+\overline{B})\nonumber\\&=&(A+B)\overline{AB}=\overline{\overline{A+B}+AB}
    ※ A・/A=0, B・/B=0
    と、いろいろに変形でき、それぞれで回路を実際に作ることができます。
    それらの違いは、１：ゲート数、種類＝コスト、手間　　２：ゲートの遅延による動作速度　です。

    組合わせ回路の基礎

    何本かある入力を決めたら、一意に出力がきまる回路を組合わせ回路といいます。 それに対して、直前までの動作の履歴が影響するものを順序回路といいます。
    ここでは先に順序回路の代表例をみて、その後組合わせ回路をみます。

    入力信号が１本以上、出力信号が１本以上あって、その関係を規定して、回路を設計します。 ここでは、例を交えて、比較的簡単な組み合わせ回路見てみましょう。

    加算回路

    ２進数の加算回路を考えます。

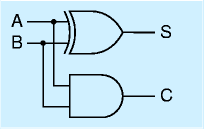    ハーフアダー 一桁分の加算回路をつくって、これをつないで複数桁の回路を構成してみます。 まず、２進数の一桁通し、ＡとＢの計算を考えると、
    A B S C 備考
    0 0 0 0 0+0=00
    0 1 1 0 0+1=01
    1 0 1 0 1+0=01
    1 1 0 1 1+1=10
    となります。Ｓは和、Ｃは繰上がりを意味します。
    これまで出てきた論理素子と照らし合わせると、丁度良く、S=A XOR B、C=A AND B です。
    これを回路図で表すと右図のようになります。この回路をハーフアダーと呼びます。

    どこが「ハーフ」かというと、複数桁の演算をするためには、繰上がりの処理もできなければなりません。 これに対して、フルアダーと呼ばれる回路は、入力はＡ、Ｂに加えて下からの繰上がり入力Ｃiの３本になり、 出力はＳ、繰上がり出力Ｃoとなります。

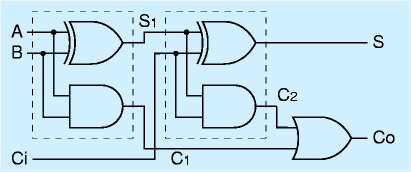    フルアダー 真理値表は次のようになります。
    CiA B S Co備考
    0 0 0 0 0 0+0+0=00
    0 0 1 1 0 0+0+1=01
    0 1 0 1 0 0+1+0=01
    0 1 1 0 1 0+1+1=10
    1 0 0 1 0 1+0+0=01
    1 0 1 0 1 1+0+1=10
    1 1 0 0 1 1+1+0=10
    1 1 1 1 1 1+1+1=11
    見方を変えると、Ｓは「A,B,Ciで奇数本が１のとき１」、Ｃoは「同、２本以上が１のとき１」と見ることもできます。
    これを先ほどのハーフアダーを使って構成した例を右に示します。
    １段目：(C1,S1)=A+B
    ２段目：(C2,S)=S1+Ci
    追加：Co=C1 OR C2
    となっています。
    真理値表で細部を確認します。
    CiA B S1C1 S C2Co
    0 0 0 0 0 0 0 0
    0 0 1 1 0 1 0 0
    0 1 0 1 0 1 0 0
    0 1 1 0 1 0 0 1
    1 0 0 0 0 1 0 0
    1 0 1 1 0 0 1 1
    1 1 0 1 0 0 1 1
    1 1 1 0 1 1 0 1
    XORをこの回路のようにトーナメントのように接続すると、入力全体の「１の数が奇数か」を出力するようになるため、Ｓの出力に、また、どちらかの演算で繰上がりがでれば、繰上がりという構造になっています。

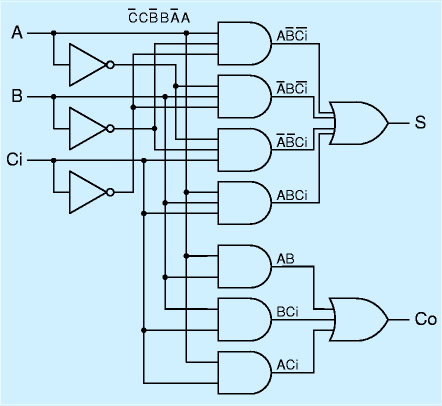    フルアダー フルアダーにはもう一つの構成があります。真理値表から直接、
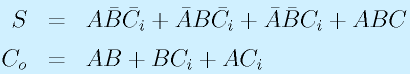
    S&=&A\bar{B}\bar{C_i}+\bar{A}B\bar{C_i}+\bar{A}\bar{B}C_i+ABC \nonumber\\ C_o&=&AB+BC_i+AC_i
    という論理式を導き右図のような回路を構成する方法です。先の回路に比較した利点は、数学的に対称的ですっきりしていることに加え、演算速度の向上が期待できることです。複数桁の演算をする場合、回路にCi入力がされて、Coから抜けて、次の段の演算が行われるため、入力→Coが早い方が速度が上がります。前者はA,B入力からはXOR, AND, ORで３段、後者の回路ではANDとORの２段の経路になっているため、後者のほうが速くなると期待されます。

    デコーダとマルチプレクサ

    デコーダ 汎用のＴＴＬやＣＭＯＳロジックＩＣの類は、基本的なロジックゲート、組み合わせ回路、順序回路のいろいろな物がシリーズになっています。上記の加算回路は算術演算系のもので、加算回路の他に小規模ですが乗算回路もあります。 そのほかに、一致検出回路や大小比較回路（８ビットと８ビットの一致、大小など）などもあります。 こういった組み合わせ回路のなかでラインナップが多いものに、デコーダとよばれるグループがあります。

    デコーダは、数値を数ビットの２進数で表しているような状態（コードになった状態）の信号を、たとえば０〜ｎ番の信号のどれかがＨになるように分解します。

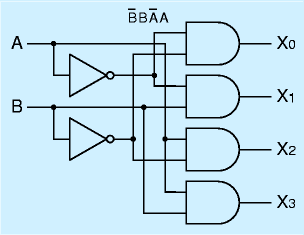
    右図はもっとも単純な部類のデコーダで、通称２to４デコーダなどと呼ばれています（入力２本、出力４本）。
    回路がごちゃごちゃしてきてわかりにくくなっていますが、論理式で書くと
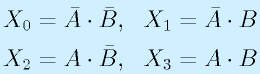
    X_0=\bar{A}\cdot\bar{B},~~X_1=\bar{A}\cdot B\nonumber\\X_2=A\cdot\bar{B},~~X_3=A\cdot B
    となっています。真理値表は、
    ABX0X1X2X3
    001000
    010100
    100010
    110001

    （普通のＩＣの説明書では１はＨ、０はＬで記載されています。）
    のようになります。つまり、入力Ａ(上位)，Ｂ(下位)の２桁の２進数と見なして、それに対応するX0〜X3のどれか１本だけが１になります。
    たとえば、このあとで出てくる順序回路のカウンタと呼ばれる回路は、一般に２進数でカウントアップしていく回路です。 それを加工して、順序にランプを光らせたりしたいときには、また、順に回路を動かすためのタイミング信号を作りたいときなどは、カウンタにこのデコーダをつなぐことで、順に出力が１になるような信号群を得られます。

    そのほか、デコーダには７ｓｅｇデコーダと呼ばれる品種もあります。これはディジタルの代名詞とも言うべき、「日」型の数値表示をするためのもので、２進数４ビットの信号をいれると、あのランプを駆動するのに適当な信号７本を出力します。
    また、デコーダは、信号が「有効」のときにＨになるもの、と「有効」のときにＬになるものがあります。使い道に応じて選定します。

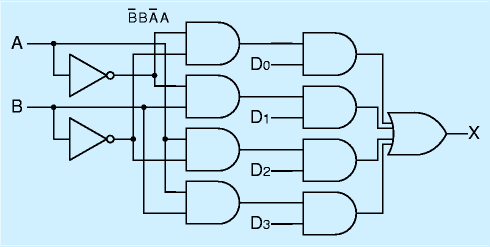    マルチプレクサ（セレクタ） このデコーダを応用した回路に、マルチプレクサ（セレクタ）と呼ばれる回路があります。

    右図のように、デコーダのうしろに、ANDとORからなる回路がついています。

    たとえば、A=0, B=0 の場合、先のデコーダ部分の動作としては、X0が１，のこりは０になります。
    そのあとの４つのANDは、それぞれ、
    X0D0X0・D0
    000
    010
    100
    111

    の動作になりますが、この見方を変えると、

    とも見ることができます。
    さて、X0〜X3は、A,Bに応じて、１本だけ１になります。ということは、４個のANDの出力は、１本はD?、のこりは０です。 これをORすると、０は関係ないので、D?が出力にでてきます。
    たとえば、A=0, B=1の場合、X1のみが1になり、D1が出力にでてきます。
    以上をまとめると、
    ABX
    00D0
    01D1
    10D2
    11D3

    となり、いわば、ＸはD0〜D3をA,Bで選んだ出力になっています。
    このような動作をするものを「マルチプレクサ」と呼びます。また、単純にセレクタと呼ぶこともあります。

    この逆で、デマルチプレクサと呼ばれる回路もありますが、あまり使われることはありません。

    カルノー図による論理回路の設計

    特殊なデコーダを作る場合など、組み合わせ回路を設計する際に、複雑な論理式から回路を起こすことは容易ではありません。
    一番簡単な方法は、デコーダのあとに、必要な信号のみを選んでＯＲする方法です。入力→デコーダで、すべての場合を網羅した信号群が得られます（ｎ入力の場合２のｎ乗本）。ここから、出力を１にするすべての場合を選ぶわけです。ところがこの方法は必用以上に冗長になる可能性が高く、その結果、複雑でコストがかさみ、動作の遅い回路になりかねません。
    そこで、普通は目的の論理式の段階で式を簡単化し、これをもとに回路を設計します。

    この式の簡単化は直感的には慣れても難儀します。これを図式で簡単にする手段に「カルノー図」という方法があります。

    フルアダーの繰り上げ信号Ｃの真理値表
    CABX
    0000
    0010
    0100
    0111
    1000
    1011
    1101
    1111

    を例題に、カルノー図をつかってみます。

    まず、真理値表から、表を作図します。
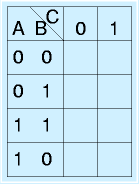
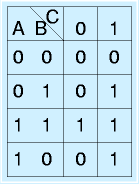
    カルノー図：基本枠 カルノー図：記入例
    まず、上図左のように枠をつくります。真理値表に似ていますが、左端と上端に入力をならべ、かつ、左端のように二つの変数を並べる場合、一般的な真理値表とは場合の順番が異なります。
    ここに、真理値表や、論理式で定義された論理を０１で書き込んでいきます（上図右）。

    つぎに、「１だけからなるなるべく大きな長方形領域」をこの枠に書き入れ、すべての１が囲まれるようにします。
    重要な点は、「１だけの領域」「なるべく大きく」「長方形」「複数の長方形ですべてをカバー」、加えて「長方形同士は重なってもよし」です。さらに、この長方形にはルールがあります。
    基本的に、
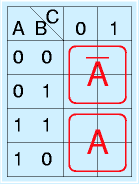
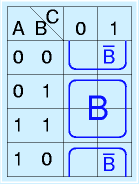
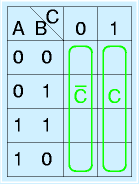
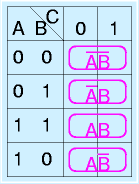
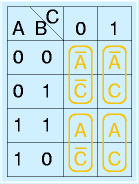
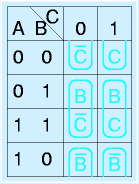
    カルノー図：Ａ領域 カルノー図：Ｂ領域 カルノー図：Ｃ領域 カルノー図：ＡＢ領域 カルノー図：ＡＣ領域 カルノー図：ＢＣ領域
    に示す２×２、４×１、１×２長方形、もしくは、１×１のみを使用します。

    最後に、選んだすべての長方形に対応する論理式を書き並べ、ORします。

    例：
    カルノー図：記入例 カルノー図：記入例
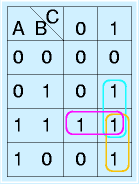
    囲んだ領域はそれぞれ、AB, AC, BC の領域です。なので、今回の題材を式に表すと、
    X=AB+AC+AB
    になります。

    このように、カルノー図は勘と経験が必用な論理式の圧縮作業をビジュアルに行うことができる便利な方法です。 ただ、手書きをするには４入力くらいが限度ではないかと思われます。

    順序回路の基礎

    組み合わせ回路は入力が決定すれば、出力はその場で決まりますが、回路によっては、直前の影響をうけたり、最後の操作を覚える物があります。こういった回路を順序回路と呼び、「フリップフロップ」（ＦＦ）と呼ばれる回路がその代表です。

    ＲＳフリップフロップ

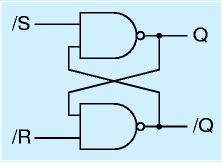    RS-FF もっとも単純な順序回路の一つが、右図に示すＲＳＦＦです。「リセットセットフリップフロップ」の略です。
    この回路は、入力の最後の操作を記憶します。

    ＲＳＦＦは/S, /R, Q, /Q端子と名前がついていますが、見て分かるように対称です。
    それぞれのNANDゲートに注目すると、NANDは２入力ともＨなら出力はＬ、どちらかがＬなら出力はＨになります。
    その性質を考慮すると、/SをＬにするとＱがＨに、/RをＬにすると/QがＨになります。
    （出力を「Ｈ」にするために、「Ｌ」にしなければならない入力なので「／」をつける）

    さて、/S, /R両者ともにＨの場合です。
    仮にＱがＨだったとします。下のNANDはH-Hが入力されるため、出力はL、/QはLになります。これが上のNANDに入力されるため、上のNANDはH-Lが入力されるため、NAND出力であるＱはＨになります。これは最初の仮定と同じであるため、この状態を保つことがわかります。
    同じようにすると、/S=/R=Ｈのときは、直前のQ, /Qを保存することがわかります。

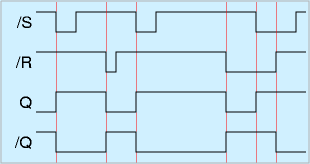    RS-FFのタイミングチャート 組み合わせ回路は入力だけできまるため、真理値表だけでその動作が記述できましたが、順序回路はそれまでの動作の履歴も関係するため、タイミングチャート（タイミングダイアグラム、タイムチャート）と呼ばれる図も使用します。
    この図では右方向が時間が進む方向、上下にディジタル信号のＨ／Ｌ、１／０をとります。つまり、信号の時間変化をグラフにしたものです。

    基本的に、/Sもしくは/RをLにすると、QがHもしくはLに設定されます。そのため、「セットしたりリセットする」フリップフロップの基礎です。なお、両方同時にＬにした場合、どちらを先にＨに戻したかで決まります。

    RS-FFの派生品はいろいろありますが、もっとも重要な物を次で触れます。

    Ｄフリップフロップ

    D-FF RS-FFにいろいろと手を加えて作られる物にＤフリップフロップがあります。

    D-FFは、覚えるべき入力は一本ですが、CLKという端子の信号がＬからＨになった瞬間（「立ち上がり」といいます）のＤの状態を次の立ち上がりまで覚え続けます。

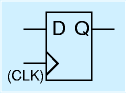
    D-FFはよく使うため、専用のシンボルが用意されています。それが右図です。「＞」記号の端子はCLKであると決められているため、敢えてCLKと書くことはほとんどありません。CLK端子、D,Qの３本です。

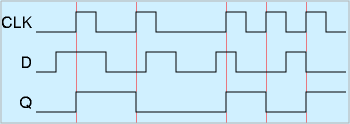    D-FFのタイミングチャート タイミングチャートは右図のようになります。
    縦線を引いたところは、CLKのち上がりです。 CLKとCLKの合間にはどれだけ変化しても、CLK立ち上がりの瞬間できまります。

    このＤＦＦは信号一本をCLKのタイミングで覚えるという特性のため、最近のディジタル回路でよく使われるようになってきました。

    なお、実際のＩＣなどの種類にもよりますが、ほぼ同時にCLKが立ち上がり、Dが変化した場合は、立ち上がり直前のＤの値を取り込むことが一般的です。

    カウンタ

    カウンタ さきほどのＤＦＦを並べると、並べたビット数の記憶回路になります。
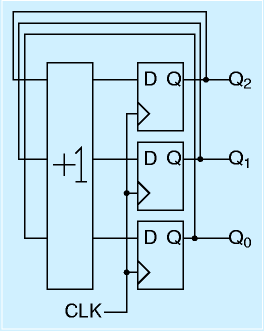
    これに演算回路を組み合わせると、いろいろな回路が作れます。その代表例がカウンタです。

    カウンタはDFF群と、「＋１」する回路で構成されます。ある時点で、全ビットで「ｎ」を表していた場合、＋１回路の出力は「ｎ＋１」になっています。ここで、CLKがくると、ＤＦＦ群が「ｎ＋１」を覚えます。これを繰り返すとカウントアップしていきます。

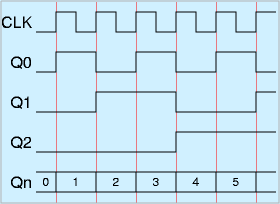    カウンタのタイミングチャート例 タイミングチャートはシンプルで、CLKの立ち上がり毎に値が増えます。
    実用的なＩＣ、回路では、この他に値を０にするクリア、またある値に設定できるプリセット、などいろいろ機能が普通はついています。
    なお、「＋１」回路はちゃんとした加算機ではなく、より単純なロジック回路で構成可能です。

    シフトレジスタ

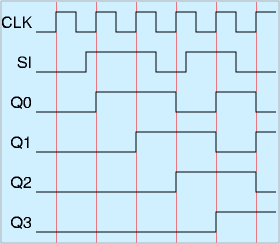
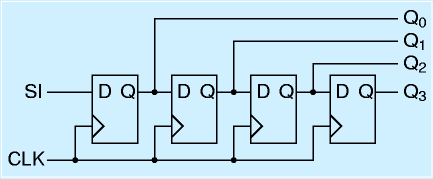    シフトレジスタ 同じく、DFFの応用回路で有名な物にシフトレジスタがあります。右図に示すようにDFFを直列につなぎます。 このとき、タイミングチャートに示すように、Q0〜Q3は初段の入力SIを順次送っていくような動作がになります。 シフトレジスタのタイミングチャート例 多くの情報を送る場合、一つの方法は線をたくさん並べることですが、時間方向に詰める方法もあり、このシフトレジスタで、時間毎に送られてきた情報をばらばらにすることもできます。


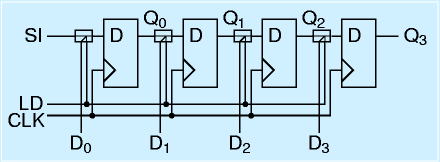
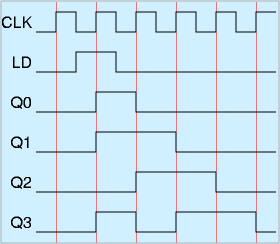    シフトレジスタ シフトレジスタのタイミングチャート例 逆に、複数の入力の信号を、直列にするためのシフトレジスタもあります。LD端子がＨの場合に、DFFは外部からの入力を取り込みます。LD=Lならば、直前のDFFの出力を送ります。

    最近のパソコンまわりの通信手段はこのような信号の送り方が主流です。

    パイプライン型回路



    熊谷正朗 [→連絡]
    東北学院大学 工学部 機械知能工学科 RDE
    ［｜　］