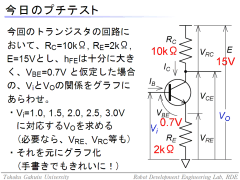
 Q:右図参照。
Q:右図参照。
このページはプチテストやレポートの問題、解答、解説を掲載するページです。
プチテストのときにわからなかったことは、必ずなんとかするようにしましょう。
Q:別紙参照
プチテスト (2012/07/23, 266,036 bytes)
A(1):
オームの法則で、E=IR, I=E/Rにて、I=0.05[A] (50[mA])となります。
電力は、P=EI=RI^2で、P=0.25[W] (250[mW])です。
A(2):
分圧の式により、30k/(10k+30k)×4=3[V]です。
A(3):
まず、12kの直列2本が合計で24[kΩ]で、これと24kが並列つなぎなので、全体で12[kΩ]になります。
※同じ抵抗を2本並列の場合1/2になる、(24*24)/(24+24)、1/R=1/24+1/24 など。
A(4):
この回路は反転増幅回路で、増幅率は39/10=3.9倍です。厳密には、電圧は−3.9倍になりますが、3.9倍という解釈で問題ありません。(負号は意識さえしていれば、最後に考えればよい)。
A(5):
SはXORで、1,0が入力されたので1(H)に、CはANDなので、0(L)になります。
※質問は出ませんでしたが、問題に誤植があり、1(H)・0(H)となっていました。答えを1・0で書いた答案はそちらを優先し(1(H) 0(H)がいくつかあった)、H・Lのみで書いた人はH・Lを優先して採点しました。
解説:
内容的にはメカトロIの計算問題です。メカトロIIは、メカトロIIですが、基礎数学に算数の計算もあるように、このあたりは当然できる、という前提の科目です。試験もまた然り。
A:
まず、各部の電圧の関係を式にします。
![]()
![]()
![]()
あとは計算するだけです。
| Vi | VRE | VRC | Vo |
| 1.0 | 0.3 | 1.5 | 13.5 |
| 1.5 | 0.8 | 4.0 | 11.0 |
| 2.0 | 1.3 | 6.5 | 8.5 |
| 2.5 | 1.8 | 9.0 | 6.0 |
| 3.0 | 2.3 | 11.5 | 3.5 |
トランジスタ1本でもこのくらいの増幅ができることを覚えておくと、便利かもしれません。
A(1):
シリーズ型の電源回路(三端子レギュレータなど)です。「電源回路」での電圧降下は(15-5)=10[V]で、電流はそのまま500[mA]流れています(実際には、電源回路そのものの取り分もある)。
そのため、損失=熱になる電力は10×0.5=5[W]です。
効率は出力が5×0.5[W]、入力が15×0.5[W]であるため、0.33(33%)となります。この7.5[W]-2.5[W]でも損失が計算できます。
A(2):
MOSFETは、オンのときは微少な抵抗として振る舞います(IDSを流しすぎるとずれますが)。
なので、この問題は、単に0.1[Ω]の抵抗に電流が1[A]流れたら?という計算です。
P=EI=RII=0.1×1×1=0.1[W]になります。
効率の計算のために、入出力の電力が必要です。入力は単純に 10[V]×1[A]=10[W]。出力は、10[W]いれて0.1[W]が無駄になったので、9.9[W]出ていると考えられます。そのため、9.9/10=0.99(99%)となります。
A(3):
この場合、どこで熱がでるかを考えます。オペアンプが動作するためにも電力はいりますが、それは無視しましょう。
そうすると、正の出力を出すためには、+15[V]からオペアンプを通して、+10[V]がでる、と考えます。-15[V]端子にはさしあたり電流は流れません。
と考えれば、(1)と考え方は同じです。熱になる電力=(15-10)*0.03=0.15[W](150[mW])、効率=(10×0.03)/(15×0.03)=0.67(67%) となります。
採点は、熱の計算で1点、効率の計算で1点としました。
非常に気になっていることが、「四捨五入ができなさすぎる」ことです。0.666=0.66と書く例が案外多く、また、0.333=0.334とした例もありましたが、切り上げも間違いです。
回路で電気をあれこれするとき、ときとして、実際に必要な電力を上回るような電力が無駄となり、熱になることがしばしばあります。多くの場合は、「無駄」という面よりは「熱くなる」という面が問題となります。パワー回路に限らず、実用的な回路を設計製作するときは「熱」に気をつけた方がいいでしょう。
 解答用紙 (2012/07/23, 151,715 bytes)
解答用紙 (2012/07/23, 151,715 bytes)
計算例 (2012/07/23, 33,843 bytes)
Q:右図参照(ωの単位は[rad/s])。
基本的に、抵抗を2本つなぐときに両者に大きな差がある場合は、抵抗の直列つなぎは「大きい方」の値に、並列つなぎは小さい方の値に近くなります。1[kΩ]と1[uF]はω=1000のときに同じ大きさのインピーダンスを持ち、これよりもωが小さくなるほど、Cのインピーダンスが大きくなり、ωが大きくなるほどCのインピーダンスが小さくなります。
と、考えると、直列では低いほうで、並列では高い方で、合成インピーダンスとコンデンサのインピーダンスが近くなるという現象は計算しなくとも想像がつくようになります。
採点は、インピーダンスについては出題時に解説したのでノーカウント、その他で、1セットできていれば1点、という換算(その他補正あり)。
レポートは遅れてでも出すべき。 過去に本科目を落ちた学生さんの多くはレポートさえ出していれば、という状況だったりします。
課題:
課題: