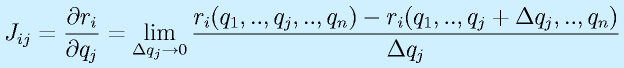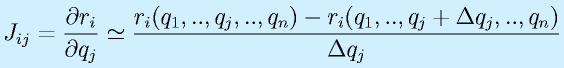マニピュレータ
[| ]
最終更新: 2018/04/17 19:36:25
心 得
主要なロボットの一つであるマニピュレータを扱います。
マニピュレータはその名?の通り、腕ロボットが良く知られていますが、マニピュレータの理論は歩くロボットの脚にも適用できます。
腕ロボットが土台が動かない(動くことももちろんあります)ところで手先を動かすのに対して、脚ロボットは動く胴体を脚で支え、むしろ脚先が地面に接していると、そこが固定点になります。
いずれにせよ、多数のアクチュエータ(駆動装置)とリンク(剛体の構造物)がつながっていて、それぞれのアクチュエータを動かすと全体が動く、という構造です。
ここでは、マニピュレータを数式化して解析するに辺り、座標系を設定し、各関節を動かすと手先はどう動くか、逆に手先の目標を設定したときに各関節をどうしたらいいかについて検討します。
座標変換で一通りやった座標変換の理論をばんばん使いますので、少しでも座標変換に行き詰まったらすぐに復習するようにしてください。
マニピュレータの機構
マニピュレータを数式にのせるには、まずその機構を確認する必要があります。
マニピュレータは形があり、重さ・慣性モーメントがあり、すべてを厳密に表現すると大変ですが、ここではリンク(棒)と関節に単純化してみます。
人を書く前に棒人間を書いてみましょう(謎)。
関節の種類と表記
ロボットは、剛体の部品がいくつかあって、それらが相対的な運動をすることで動きをつくり出すものとみることができます。
相対的な動きの仕方にはいろいろな種類があります。隣同士の部品が接したまま相対的に動く場合を考えると、ある軸を中心に回転するもの、スライドするもの、人間の股関節や肩関節のような球面で接するボールジョイントなどです。
その中でも、ロボットでは
- 1本の軸を中心に回転だけする関節(回転関節)
- ねじれたりすること無く、一方向に位置だけが変わるようにスライドする関節(直動関節)
- ボールジョイント
が主に使われます。
ただし、モータなどで直接駆動するのは、回転関節と直動関節が大半です(そのうち回転が大半)。
現在使われているアクチュエータは基本的に回転(一般的なモータ類)と直動(リニアモータ、油圧シリンダ等、回転モータ+ネジ等)で、単体では一方向の駆動のみができるためです。
球面状のモータなども開発されていますが、出力やコストにまだ見合っていません。
三つ目のボールジョイントは、棒の両端に取りつけて、二つの関節の間の距離のみをきめる用途などでよくつかわれます。
両端とも駆動しないため、姿勢はきめられません。
ラジコン自動車を組み立てたことがある人は、たぶん見覚えがあるとおもいますが、ラジコンサーボとステアリングのパーツをつなぐ部分によくつかわれています。
この用途のため、「ロッドエンド」と呼ばれる部品が販売されています。
そのほか、円筒の穴に丸棒を刺したようなジョイントも考えられます。
これは回転とスライドとができますが、案外使い道がなく、使われることは稀です。
さて、実際にロボットの機構を単純に書くために、各関節を記号化します。
3次元のロボットを2次元で書くため、いくつかの書き方があります。
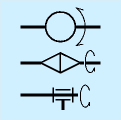
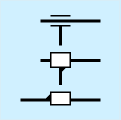
それらを右の図に合わせて示しました。
回転関節については、一番上は紙面に垂直なもの、二番目と三番目は紙面上に軸がある場合です。二番目と三番目は同じ回転を表しますが、本によって違ったり、前者は構造的に腕の途中にある関節(ねじれる関節)、後者は屈曲する関節として書分けている場合もあるようです。
スライドについては、一番上をよく見掛けますが、二番目、三番目もあります。三番目は伸縮を表します。
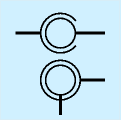
ボールジョイントについては、そのまんまです。書くのが面倒だと、下の図のように二重丸にすることもあります。なお、この図では大きめに書いてありますが、ボールジョイントは駆動のない補助的な関節であることが多いため、回転などより小さめに書いた方が見やすくなります。
なお、これらの表記は平面で書く場合の表記法です。立体感を得やすいように鳥瞰図のように斜め方向から見た図などでは、これらの記号を使うこともありますし、円筒で回転関節を表すこともあります。
いずれにせよ、見せたい相手と、書いた本人が、ちゃんとわかるように統一して書きましょう。
表記例
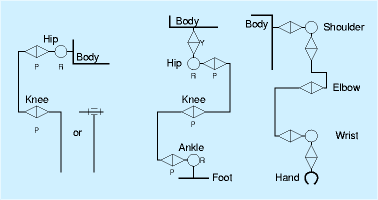
右図に機構の記述例を示します。左が上で示した記述法で、そのうち左端の4脚ロボットの足の例を斜めから見たものを右に示します。直感的には、斜め方向から立体的に書いてある方がいいのですが。
このような図を書く場合に注意すべき点は、なるべく実態を表すようにすることです。
関節の数と順序があっているのは当然として、関節の軸間の関係がわかるようにすることが重要です。
たとえば、これらの図では、複数の回転関節の複合である股関節や足首関節などを記述するため、
各回転関節の軸が一点で交わることを明記しています。
ちなみに、このように回転軸をクロスさせると後述の座標変換や運動学の演算式が簡素化します。
ただし、実際にこのようなメカを設計製作することは容易ではありません。
座標系設定とその関係
マニピュレータを数式で解析する場合、おそらくもっとも関心が高いのは
- すべての関節角度が与えられたとき、手先、足先がどの位置になるか
- 手先、足先をある位置に持っていきたいときに、関節角度をどうすればいいか
といえます。
これらの演算の詳細は次節に送るとして、まずはその下地をつくります。
これらの問題を解くには、最終的には、
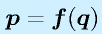
という形で、すなわち、ロボット上の注目点(手先など)の位置と姿勢(位置だけのこともありえます)
p が、各関節の角度(回転)や移動量(直動)の組
q の関数(複数の関数:
p の次数だけ)
f で表す必要があります。
もちろん、気合いと根性で座標変換を繰り返して求めることもできますが、注目点をどこにおいてもいいように、同次変換行列の組でロボットを表してみます。
修正Denavit-Hartenberg記法
ここで紹介する方法は「修正 Denavit-Hartenbergの記法」と呼ばれ、ロボット関係の教科書ではよく載っている方法です。
論文でもDHパラメータと表がのっているだけで終わることもあります。
まず、ロボットの各リンクごとに座標軸を設定します。リンクや座標軸の番号は以下のように定義します。
- 基準(腕ロボットなら地面に固定、脚ロボットなら胴体など)となる部分をリンク0として、手先に向かって各リンクに 1,2,..n と番号をつける。
- リンク i-1 と リンク i の間の関節を、関節 i とする。つまり、関節番号は 1..n となる。
- 各関節に関節軸を定義する。回転関節なら回転軸を、直動関節なら直動方向に平行な直線を関節軸i とする。
次に座標系を各リンクごとに設定します。リンク i には、座標系 i を固定します。
座標系は次のように設定します。
- Zi軸は関節軸iに一致させる。
- Xi軸は、Zi軸とZi+1軸の共通垂線にする。
- ZiとXiの交点が原点Oiになって、ZiとXiの外積でYi軸が定まる。
- 付帯1:ZiとZi+1が平行な場合(非常によくあるケース)はXiが定まらない。そのため、あとで述べる同次変換行列がなるべく単純になるように適宜きめる(骨格となるような軸上など)。
- 付帯2:座標系0は座標系1の基準状態と一致させる。
- 付帯3:座標系nでは、Znを関節軸nと一致させ、関節nが基準角度のときに、Xn-1とXnが平行になるようにする。
- 付帯4:根本的に、なるべく行列が簡単になるように(それが身のため)。
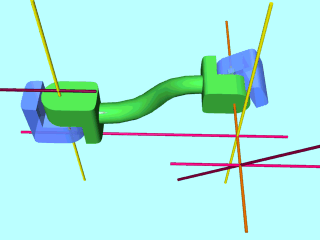
具体的に右の図で確認します。
ロボットのリンクがこんな形をしていることは稀ですが(必然性なくこんな設計したら普通は上司や量産部や工場に怒られます:-))、説明上、こんな形に書いてあります。
緑のリンクが、着目するリンク、リンク i-1 です。i-1に着目するのは、パラメータの番号設定の関係です。
青のリンクはそれぞれ一個前のリンクi-2と、一個あとのリンクiです。
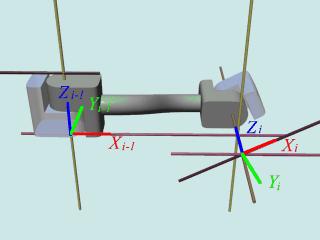
Zi-1, Ziの座標軸は上の規定通り、回転軸に設定します(ぞれぞれ、左の黄色線とオレンジの線)。
次に、Xi-1軸ですが、上から三番目の図に赤で書いたように、2本の回転軸の両者に垂直な線を見つけて、そこに設定します。
2本の軸が平行な場合は、そういう線は無数にありますが、それ以外の場合は、必ず一本のそういう線が存在します(別の見方をすれば、2本の線を最短距離で結ぶ線です)。
あとは、Yi-1は自動的に決まります。
ちなみに、Xi, Yiについては次のリンクの形に依存するので、ここでは想像して適当にきめてあります。また、関節iは適当な角度にまがっています。
さて、この場合の、座標系i-1から座標系iまでの、同次変換行列を求めてみます。
座標系i-1から座標系iまでは、次の4つの変換を組み合わせることでたどれます。
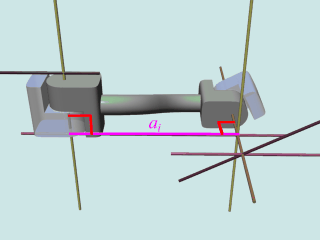
- Zi-1とZiを結ぶ共通垂線の長さ ai だけXi-1方向に平行移動(三番目の図)
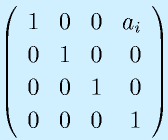
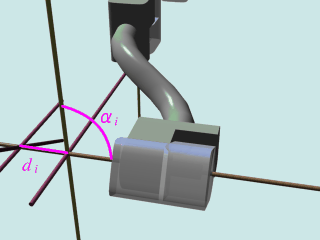
- Zi-1がai平行移動した線(右の黄色)と、Zi軸の成す角度αだけ、Xi-1軸を回りに回転(四番目の図)
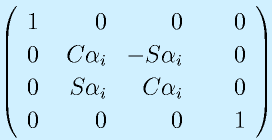
- Xi-1軸がXi軸の位置に来るように、回転したあとのZi-1軸(Zi軸に同じ)の方向にdiだけ平行移動(四番目の図)
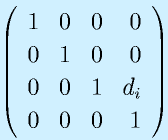
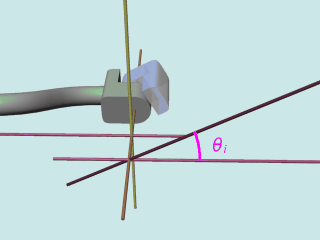
- ここまで移動してきたXi-1軸がXiに一致するように、Zi-1軸まわりにθi回転させる(五番目の図)
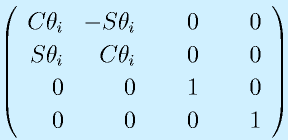
なお、回転に関しては正の方向に注意する必要があります。
また、本によって、aiではなくai-1を使っているなど、微妙に複数ありますが、ここでは授業の教科書に統一します。
最終的に、これらを順に掛け合わせて、座標系i-1から座標系iに至る同次変換行列を得ます。
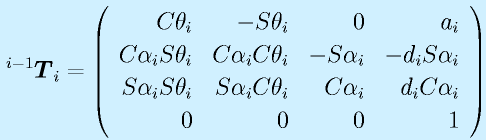
この表記法は、リンクを、となりのリンクとの関係も含めて、四つのパラメータ a,α,d,θで表す方法です。
同次変換行列は12個の有効な要素がありますが、それを4パラメータで済ませることができます。
また、上式は一見するとややこしいのですが、実際にはそれぞれの値が単純になります。
- ai=0の場合
リンクの長さがゼロということは不思議に見えますが、計算を簡単にする意味で、ロボットを設計するときに見られる場合です。二方向、三方向に曲げたい関節は、回転関節を2個、3個組み合わせて作りますが、そのときに回転軸が1点でクロスするように中間リンクを設計します。
そういう場合に、ai=0がでます。
- αi=0の場合
回転軸が平行な関節が続く場合です。4つ以上連続して並べると無駄ですが、3個までは連続して並べる場合があります。逆に、3個の連続した関節があり両端は複数の方向に曲がるような場合(肩−肘−手首 or 股−膝−足首)、複数の方向の中から中間の関節と同じ向に曲がる関節を意図的に並ぶようにすると、計算が楽になります。
例、股関節 Roll,Pitch,Yaw、膝P、足首R,Pの時、(Y-R-P)-P-(P-R)と、Pを膝側に集める。
- αi=90度、180度
普通のロボットを設計する範囲では、αiはゼロにならないまでも、直角とか、反転とかですみます。
- di=0
構造をシンプルに設計した場合は、di=0になる場合が多いでしょう。
一般的なロボットで良く見られる回転関節の場合はθiが関節角度(元のZiの定義そのもの)、直動の場合にはdiが直動の量(直動方向にZiをとる=Zi方向に移動するdiがパラメータ、θi=0)になります。
だいたいこのような状況が多いため、同次変換行列は一般にシンプルになります。
また、これまでの内容に従って、
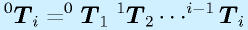
となります。
リンクiの座標系i上で規定された点、例えば腕上の特定の点を、基準座標系でどこに見えるかをこの同次変換で知ることができます。
記述例
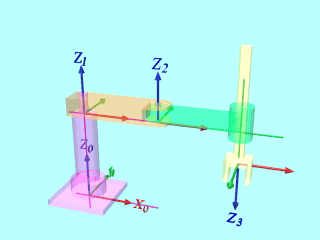
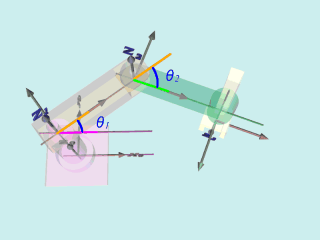
教科書にも載っている、右図に示すロボットで実際にモデルを数式化してみます。
このロボットは2個の回転関節と直動関節からなるロボットです。
動作形態としては、根本側の回転関節1・2によって、手先の水平面内での位置を決め、直動関節3によって手先を上下させることで、手先でものを搬送できます。
ただし、3次元空間で位置、姿勢をすべて決定づけるには独立した6関節(6自由度)必要であるの対して3関節しかないため、手先の位置をきめることしかできません。
姿勢はそれに連動します(手先の鉛直軸まわりの姿勢は関節1・2で決まり、手先を鉛直から傾けることはできない)。
まず、座標軸を設定します。基本的には上で示した方針で、あとは分かりやすくなるように設定します。
ちなみに、教科書にも準拠していますが、Y軸の向きが一部異なります(教科書の図は右手系と左手系がごっちゃのため、右手に統一した)。
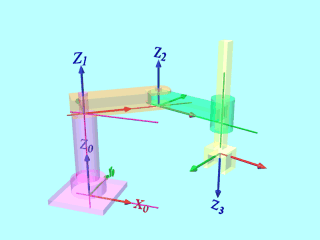
リンク番号は根本からつけますので、土台(紫)を0、上腕(橙)を1、下腕(緑)を2、手先(黄)を3とします。
Z軸は関節軸(回転軸or直動軸)にとり、X軸はZ軸の共通垂線にとります。
ここで、このロボットはすべてのZ軸が平行なので、Xはどこにとっても構いませんが、機構にあわせて、X1とX2は同一平面で土台と上腕の接合面におきました。
X3はX2と平行になるように、X0は関節角度が0(基準位置)となるときにX1と平行になるように設定しました。
なお、上述の設定では、座標系0は関節が基準位置のときに座標系1に一致するようにというガイドラインがありますが、ここではロボットの基準面に取ったほうがあとが楽そうなので、座標系0は1を土台の面まで平行移動したところにしました。
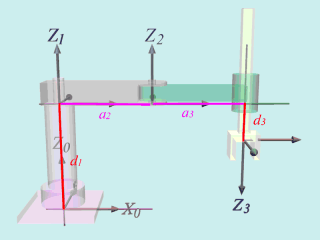
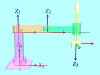
座標系が決まりましたので、DHのパラメータ出しを行います。
各リンクごとに
- 座標系0→1:
Z0軸方向にd1だけ平行移動してから、関節1の関節角度θ1だけ回転、a1=0、α1=0
- 座標系1→2:
X1軸方向にa2移動、関節2の角度θ2だけ回転、α2=0、d2=0
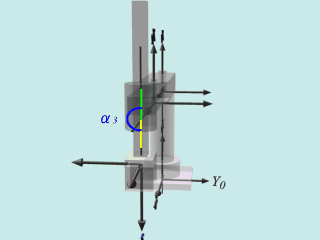
- 座標系2→3:
X2軸方向にa3移動、X2軸回りにα3=180度(π)回転、回転後のZ2軸方向(鉛直下向)にd3移動、θ3=0
となっています(右図参照)。
表にまとめると、
| リンク | a | α | d | θ |
| 1 | 0 | 0 | d1 | θ1 |
| 2 | a2 | 0 | 0 | θ2 |
| 3 | a3 | π | d3 | 0 |
ここで変数(動く部分)はθ1, θ2, d3です。
以上をもとに、同次変換行列を求めます。
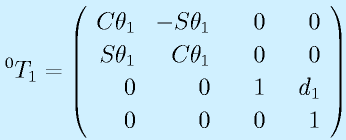
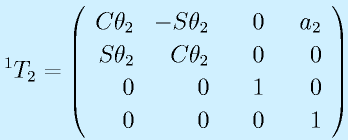
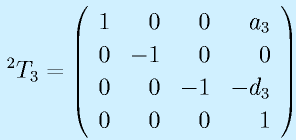
よって、土台の座標系0からみた手先3の座標系の変換は
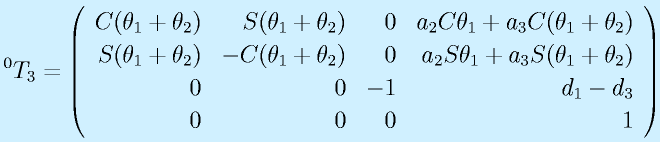
となります。
なお、この程度の機構の場合、わざわざこのDHの方法をしなくても、高校並の方法でも簡単に求まります。
それと比較してみるとよいでしょう。
運動学と逆運動学
運動学と逆運動学
ロボットを数式化する大きな目的のひとつは、ロボットを制御するに当たって、関節をどう動かしたらいいかを決定することです。
ロボットで、あるところにあるものをピックアップして、別のところに運ぶという仕事を行いたいとき(工場の製造ラインなどでありがち)、まずそれぞれの場所に手先を持っていくために各関節をどれだけ変位させればいいかを求める必要があります。一方で、現在の関節変位から手先の位置を知り、そのあとの軌道を計画したり、制御の情報にしたりすることも必要です。これらを運動学と言います。
- 関節変位(回転、直動)→手先位置・姿勢:順運動学
Forward(Direct) Kinematics
- 手先位置・姿勢→関節変位(回転、直動):逆運動学
Inverse Kinematics
数学的には、手先の位置と姿勢を表すベクトル
r と関節変位を表すベクトル
q が
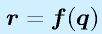
という関数群で表され、順運動学は
f 、逆運動学は
f の逆関数を求めて計算することです。
一般的にみられる(上の図のような)直列リンク型の機構では順運動学が(めんどうながらも)単純に求められ、逆運動学は簡単には求められないか、数式として得られない場合があります。
一方、並列リンク型の機構では逆運動学は単純に得られるものの、順運動学が得られない場合があります。
以下では上のロボットを例に解いてみますが、その過程に注意してみてください。
2脚ロボットのような複雑な機構の場合にも、股関節のような複合関節で回転軸が一点で交わるようにすると解きやすくなることが、わかると思います。
ためしに解いてみる
前節で出てきたロボットを例に逆運動学を解いてみます。
関節変位は
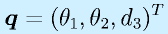
で、手先についてはその位置だけに着目して、座標系3の原点とします。
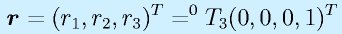
順運動学はすでにもとまっていて、
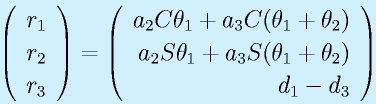 です。
です。
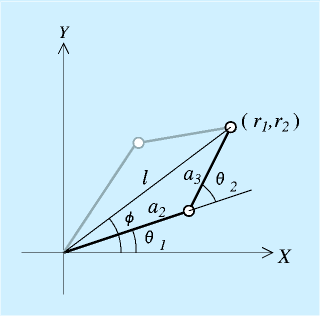 逆運動学はこれをθ1, θ2, d3について解きます。まず、あからさまに、
逆運動学はこれをθ1, θ2, d3について解きます。まず、あからさまに、
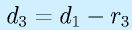
です。残りは幾何学的にみてみます。
ロボットを上方からみた図を右のように表します。ここで、手先が座標(r1,r2)に来るためには、(届くなら)関節2の位置が二通りになります。
手先の位置を別の見方で表すと、
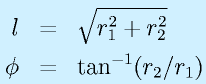
となります。また、余弦定理より
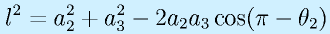
が成り立ちます。よって、
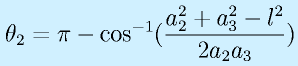
と求められます。また、
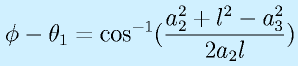
よりθ1も求まります。
※教科書の式とかなりちがいますが、cos-1を使うかtan-1を使うかの違いです。数値計算で検算してみると、教科書のθ2の式は、ちょっと怪しげな気が。θ1=φ─θ2という時点で怪しい気が。
数値的に解く
以上のように、このくらいの場合には解くことはできますが、複雑になってくると数式では解けなくなってきます。
そのような場合には、数値計算によって解を得ることができます。具体的には
- 仮の q を定める。
- 順運動学を用いて r を得る。
- 目的とする r との差を求め、それをもとに q を微修正する
- r の誤差が十分小さくなるまで繰り返す。
式で書くと
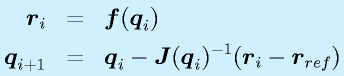
となります。ここで、修正の方向と程度を決める行列J(上式では逆行列が使用される)はヤコビ行列と呼ばれ、その各成分は
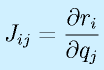
で与えらます(
q の関数群)。いわば、
q の各成分を微少に動かしたときに、
r の各成分が受ける影響を行列にまとめたものです。

速度や力に関して考えるときもこれは頻繁にでてきます。
ヤコビ行列を求める1
ここでは、今後の応用も考えて、ヤコビ行列を求めてみます。
すでに順運動学が直接的な式で求まっている場合は、それを直接微分すればヤコビ行列が得られます。
まず、運動学の式は先ほどの通り
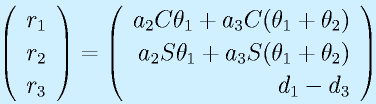
です。よって定義通りに計算すると、
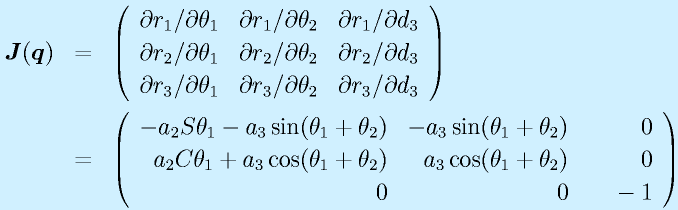
となります。
ヤコビ行列を求める2
上の方法では、 r をちゃんと計算しないとヤコビ行列は求まりません。
ここの例の3自由度程度であれば求めることはたいしたことはありませんが、ありがちな6自由度の場合は一般にはかなり悲惨な式になります。
そこで、発想を転換して、部分部分で求める方法が考案されています。
ヤコビ行列を分解した列ベクトル
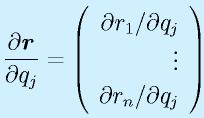
は、ある関節を動かした影響が手先座標 r にどれだけ出るか、を示したものと解釈できます(偏微分=ある変数が式に与える影響)。
そのため、当然ながらロボットの状態の影響を受ける値を持ちますが、ロボットの現在の姿勢があれば、関節一個を動かしたときの影響は、簡単に求められそうです。
こまかなところは剛体の力学の勉強し直しが必要になりそうなので、概念だけ以下に示します。
- 回転関節が手先位置に与える影響は、その軸からみた手先までの距離に比例し、方向は円周方向になる。
このとき、軸の位置、向き、手先位置をすべて基準座標系(リンク0)に変換しておく。
- 直動関節が手先位置に与える影響は、その伸縮そのものである。
伸縮方向を直前までの同次変換行列で基準座標系に変換しておく
- 回転関節が手先姿勢に与える影響は、手先姿勢の評価方法にもよるため一概に言えないが、角速度はその軸が平行である限り軸の位置は関係ないため、関節の回転角速度は手先の回転角速度そのものになる。
- 直動関節は手先の姿勢に影響を与えない
これをつかうと、「悲惨な式」をすべて求めなくても、部分的な関係(同次変換行列など)を積み重ねることでヤコビ行列を得ることができます。
速度の運動学
ここでは、マニピュレータの速度についてさらっとみてみましょう。
速度の運動学
すでに出ているヤコビ行列
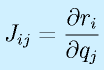
は、微少な関節の変位と、手先の変位の関係として

が成り立ちます。
両辺をその変位にかかった時間δtで割って、それを0への極限をとると、微分形式の
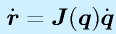
となります。つまり、ヤコビ行列は、関節の速度を手先の速度に変換する行列としてもつかえます。これは速度の順運動学です。
もし、ロボットがある姿勢の時にヤコビ行列に逆行列があれば、
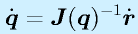
となり、「手先の速度から関節速度」がもとまります。つまり、手先の速度をきめてやれば、それを実現するための関節の速度が得られるわけです。これは速度の逆運動学です。
ちなみに、これは直列リンクなマニピュレータの場合で、位置の逆運動学がもとまるけど順運動学が求まらないようなパラレルリンクのマニピュレータの場合、立場が逆になります。
ヤコビ行列で見るロボットの特性
速度の逆運動学を得られる条件として、ヤコビ行列の逆行列があることがありました。
ある行列に逆行列があるためには、
があげられます。
前にふれた、空間で位置と姿勢を決めるには6変数が必要で、そのとき関節は最低6個あればよい、という意味は、
r と
q の数が等しいという条件を満たす最低ラインを意味します。
関節が7個などより多い場合は次に扱うことにして、ここでは
r と
q の数は等しいものとします。
では、行列式がゼロになるということはどういうことかと考えます。
すでに求めているロボットのヤコビ行列
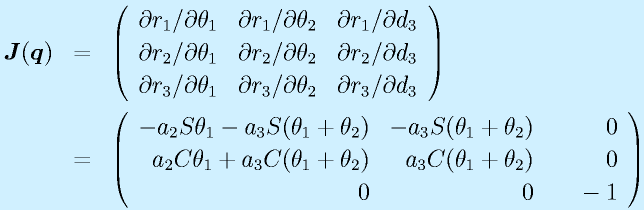
より、行列式を求めると、
\nonumber\\ &=& a_2a_3 \Sth_1 C(\theta_1+\theta_2) - a_2a_3 \Cth_1 S(\theta_1+\theta_2)\nonumber\\ &=& a_2a_3\{\Sth_1(\Cth_1\Cth_2-\Sth_1\Sth_2)-\Cth_1(\Sth_1\Cth_2+\Sth_2\Cth_1)\}\nonumber\\ &=& a_2a_3\{-(\Sth_1)^2\Sth_2-(\Cth_1)^2\Sth_2\}\nonumber\\ &=& -a_2a_3\sin(\theta_2)](eqn/manipulator.bhtml.eqn306.gif)
となります。
この式において、ロボットの構造上 a が0になることは想定されませんが、sin(θ2)=0は状況としてあり得ます。
sin(θ2)=0は2つ目の関節が真っ直ぐに伸びた状態か(θ2=0)、もしくは完全に折り畳まれた状態(θ2=π)です(後者はロボットの作りによっては無理)。
このとき、行列式が求められなくなり、速度の逆運動学が成り立たないことになります。
実際のロボットの上で、この行列式=0の意味を考えてみましょう。このロボットに限らず、人間の肘や膝を考えてもわかりますが、関節が真っ直ぐになった状態では、当然ながらそれ以上は手先を遠ざけることはできません。
手や足の場合、手首足首の関節で、位置だけならより遠くに持っていくことが出来る場合もありますが、姿勢が変わってしまいます。
それとは反対に、縮めようとすると関節を急速に曲げなければなりません(数学上はそれすら出来ないことになっている)。
このような状態を特異点、そのときのロボットの姿勢を特異姿勢といいます。機構の面からは死点ともいいます(自動車のエンジンなどでも使う)。
この特異点では、特定の方向への運動が出来なくなっています。また、特異姿勢のそばでは、ちょっとの動きをするために、関節を極端に高速に動かす必要があります。
(肘を伸ばした状態から、手首を1センチほど肩に近づけてみてください。肘関節の角度が急に大きくなることがわかります。一方、肘関節が大きく曲がった状態で手首を近づける場合はあまり動きません。)
そのため、マニピュレータに任意の作業をさせる場合は、マニピュレータの運動範囲を制限して特異姿勢に近づかないようにしなければなりません。
実際の例としては、最近みられる歩行ロボットがことごとく膝関節をある程度まげた状態で歩いているのも、一般には膝関節の特異点を避けるためです。膝関節を多少曲げておくと、膝関節を真っ直ぐに伸ばしたときに比べて関節にかかる力が大きくなります。
その観点からは伸ばしておいた方よく、人間が歩くときは膝を真っ直ぐして着地します。
しかし、歩行ロボットの制御分野ではそこまで進んでいないということになります。
疑似逆行列
世の2脚歩行ロボットは一般に脚には6自由度を持たせています。
これは足の位置と姿勢を制御するという観点でぴったりの数字です。
それに対して、一部の腕ロボットは7自由度をもっていて余分です。
これは人間の腕を単純化したときにでてくる形です。
(肩3自由度、肘1自由度、下腕のねじれ1自由度、手首2自由度)
これは手先の位置と姿勢を決めても1自由度余ることを意味し、作業する際に腕の位置をある程度選べることになります。
ところが、この1自由度余る分を何らかの形で決めなければなりません。
ほかの制約があるときは、それを組み込むことになりますが、そうでないときは逆運動学も求められずに、関節が一個余分なだけでやっかいなことになります。
そこで考案されたのが「疑似逆行列」です。
文字通り、「疑似」的に「逆行列」相当の働きをするようにしたものです。
疑似逆行列は
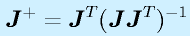
で与えられます。
ちなみに、加えられた1自由度分の制約は「全関節の動きをなるべく押さえる」という意味で、
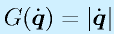 が最小
が最小
という条件です。この時、
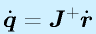
で速度の逆運動学が得られます。
補足・補遺
マニピュレータの設計にあたって
多自由度のマニピュレータを設計するに当たっては、目的の動作ができるか(可動範囲など)に加えて、数式の上である程度単純になるようにしたほうがよいと言えます。
そうすることで、運動学、逆運動学が単純になるほか、設計時のミスや混乱を防ぎやすくなります。
運動学、逆運動学はいまどきのコンピュータの性能をもってすれば、いちいち解析的に(数式として)求めずとも数値計算で間に合わせることはできますが、単純なのに越したことはありません。
ある程度単純であれば、数式を無理やり解くのではなく、上の例のように幾何学的に処理することもできます。
そもそも、ロボットの動かし方を考え、設計して動作を決めるのは人間であり、頭の中でイメージがわかないようだといい設計はできないと思われます。
これまでたびたび、「多自由度関節は軸を直交させた方がいい」と述べてきたのは、この観点によるものです。
たとえば、6自由度の腕ロボットを設計するとき、手首に3自由度を配置し(ロボットアームの先端に近いところに回転軸を寄せる)の関節を一点で交わるように、さらに肩の関節を2自由度にして1点で軸が交わるように設計したとします。
(3軸は工夫が必要ですが2軸は案外簡単)
このとき、ロボットの逆運動学は6個もθが入った三角関数ごちゃごちゃの式を解くことになりますが、これを直接解かずに、以下のような手順で各関節の角度を決められます。
- 目標として与えられた手先の位置と姿勢から、手首関節の位置を決定する。
(手首の関節角度はとりあえず放置)
- 手首の位置をもとに、肩関節と手首関節の距離を求めて、肘関節の角度を決める。
(上の例参照)
- 手首が計算された位置にくるように肩関節の角度を決定。
(Z0を軸とする極座標に変換すれば容易)
- 肩、肘の関節角度と、手先の姿勢から、手首の関節で変換すべき回転行列を求める。
(単純に、手先の行列Rに肩肘による行列の逆行列をかける)
- 手首の回転軸の構成に応じて、行列の成分を比較して角度を決定。
(オイラー角で角度を求めた例などを参照)
このように、イメージのわきやすい方法で幾何学的に求まります。
手首が直交していない場合では、姿勢の調整のために角度をいじると手先位置もかわってしまったり、複雑になり、数値計算でなければ処理できなくなることが多くなります。
加えて、手先の位置と手首の関節軸が一致するような設計がもしできれば、第一ステップも省略され、なおさら計算が楽になります。
また、手先の姿勢だけ変えるような作業をする場合に、腕全体は動かさなくて済むため、用途によっては速度的に有利になります。しかし、今度は設計や製造がたいへんになるでしょう。
プログラム実装
これまでの数学的な話では、複数の同次変換行列が求まったときに
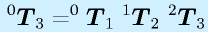
などと記載していました。
ロボットの制御をしたり、シミュレーションを行う場合には数式をプログラム化する必要があります。
そのとき、"0T3"に相当する式を手で計算してしまってから入力しなければ、と思う人がいるかもしれませんが、そんなことはありません。
"0T1", "1T2", "2T3"を個別に求める式を入力してプログラム実行時に値を出し、プログラムの上で"0T3"を計算すればよいのです。
行列演算をする関数はC言語などには標準ではありませんが、ネット上で提供されているものもありますし、行列やベクトルの計算くらいならC言語の演習の感覚でつくってしまえばいいのです。
複雑な式を間違う(計算,入力)危険を犯してあらかじめ計算するよりは、明らかに効率がよくなります。
きちんと定義した上で、中間変数はじゃんじゃんつかいましょう。
ヤコビ行列を求める3
もうひとつ、力業で求める方法が考えられます。本来の偏微分の定義より、
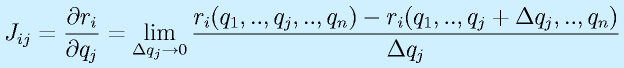
です。
微分という操作は極限という実現はできないことを考えたものなので、コンピュータのなかで微分値を使いたいときに差分という方法で代替することがあります。
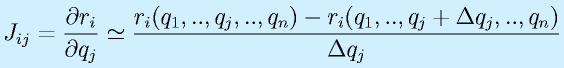
どこが変わったかというと、Δqjを0にリミットしません。そのかわり、十分小さな値にします(極端に小さくすると演算精度が落ちるので注意)。
このことを使うと、
- 運動学の式をつかって現在のロボットの関節値から手先座標を求める。
- 各関節値を個別にほんの少しΔだけ増やした手先座標を求める。
- ずらした手先座標からもとの手先座標を引いて、差をΔで割る。(関節の数だけ繰り返し)
という形で数値計算できます。
もちろん、数値計算する以上は誤差がでたり、演算精度の桁落ちの危険性があるため、そのあたりにも気配りが必要ですが、人間が計算しなきゃいけない式の数が減るという利点がこの方法にはあります。
熊谷正朗
[→連絡]
東北学院大学
工学部
機械知能工学科
RDE
[| ]





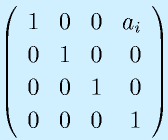
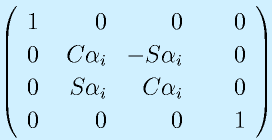
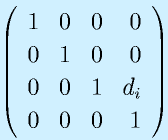
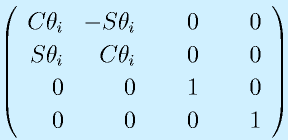
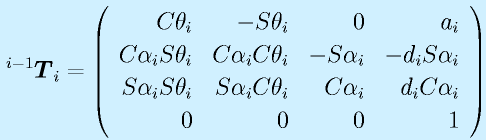
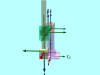

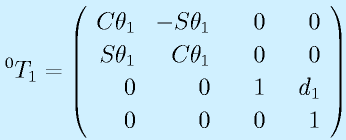
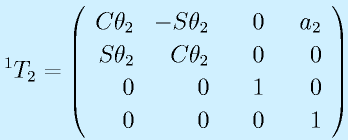
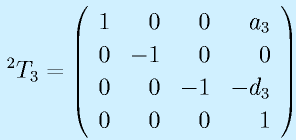
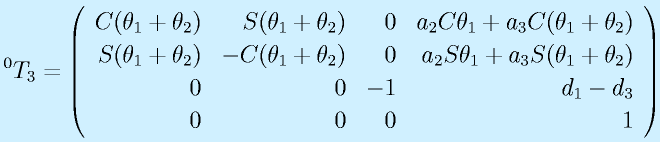
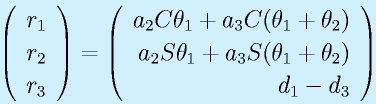 です。
です。
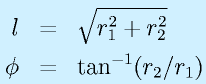
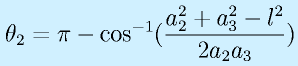
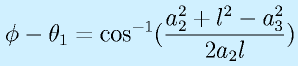
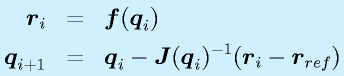
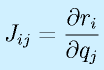
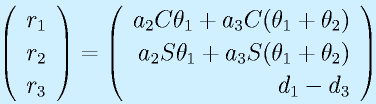
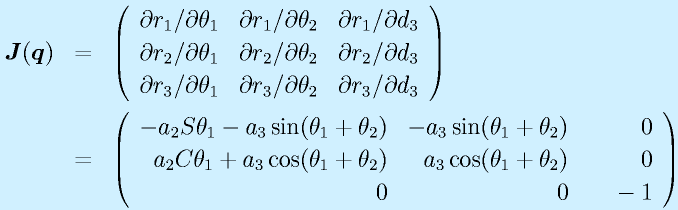
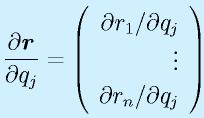
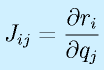
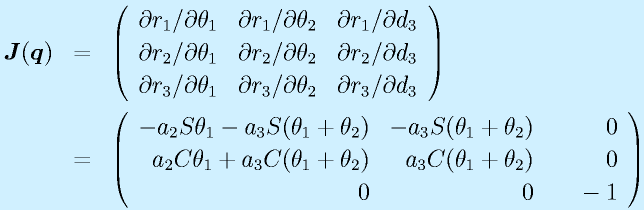
\nonumber\\ &=& a_2a_3 \Sth_1 C(\theta_1+\theta_2) - a_2a_3 \Cth_1 S(\theta_1+\theta_2)\nonumber\\ &=& a_2a_3\{\Sth_1(\Cth_1\Cth_2-\Sth_1\Sth_2)-\Cth_1(\Sth_1\Cth_2+\Sth_2\Cth_1)\}\nonumber\\ &=& a_2a_3\{-(\Sth_1)^2\Sth_2-(\Cth_1)^2\Sth_2\}\nonumber\\ &=& -a_2a_3\sin(\theta_2)](eqn/manipulator.bhtml.eqn306.gif)