つかう数学

ベクトル

ベクトル：
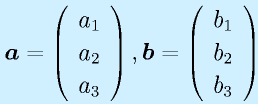
$\vect{a}=\left(\begin{array}{c}a_1\\a_2\\a_3\end{array}\right), \vect{b}=\left(\begin{array}{c}b_1\\b_2\\b_3\end{array}\right)$
標準で縦ベクトル、一般に小文字、ボールド(太文字)表記
$\vect{a}^T=(a_1,a_2,a_3), \vect{b}^T=(b_1,b_2,b_3)$
転置(T)で横ベクトル。
$|\vect{a}|=\sqrt{a_1^2+a_2^2+a_3^2}$
ベクトルの長さ(大きさ)。

用途：
ベクトルは座標や状態量を表すために使用。

２次元位置　　　 → ２要素
２次元位置＋姿勢 → ３要素
３次元位置　　　 → ３要素
３次元位置＋姿勢 → ６要素
関節の数だけ → 関節の状態量

※姿勢が入るとベクトルじゃなくなる場合が出てきます。たとえば、３次元での姿勢角度を表そうとした場合、回転させる順番で結果が異なる、すなわち ab=ba という交換法則が成り立たなくなります。けど、角速度はベクトルです(詳細はいずれ)。

ベクトルの加算、スカラ倍：
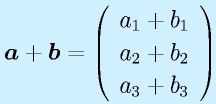
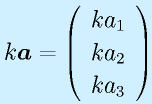
$\vect{a}+\vect{b}=\left(\begin{array}{c}a_1+b_1\\a_2+b_2\\a_3+b_3\end{array}\right)$ $k\vect{a}=\left(\begin{array}{c}ka_1\\ka_2\\ka_3\end{array}\right)$
$\vect{a}+\vect{b}=\vect{b}+\vect{a}$

ベクトルの内積：
$\vect{a}\cdot\vect{b}=a_1b_1+a_2b_2+a_3b_3=\sum_{i=1}^n a_ib_i$
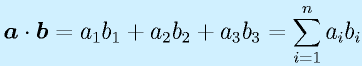
ベクトルの内積はその平行具合いを示します。２、３次元では成す角度をθとして、
$\vect{a}\cdot\vect{b}=|\vect{a}||\vect{b}|\cos\theta$
となります。そのため、「＝０」で直交を意味し、またベクトルの成す角を定義できます。
(４次元から先、成す角度という概念があるかは未確認。ただし、ロボット的には意味無し。)

ベクトルの外積(３次)：
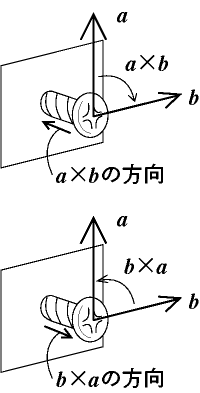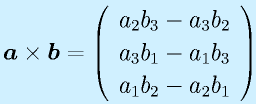
$\vect{a}\times\vect{b}=\left(\begin{array}{c}a_2b_3-a_3b_2\\a_3b_1-a_1b_3\\a_1b_2-a_2b_1\end{array}\right)$
$\vect{a}\times\vect{b}=-(\vect{b}\times\vect{a})$
順番があることに注意。
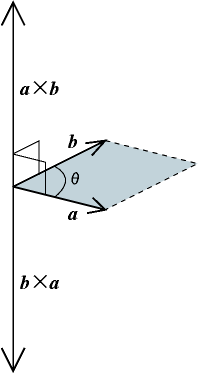
外積で得られるベクトルは、

長さ(大きさ)は２ベクトルでできる平行四辺形の面積、すなわち、２ベクトルのなす角をθとすると、
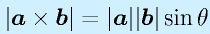
$|\vect{a}\times\vect{b}|=|\vect{a}||\vect{b}|\sin\theta$
です。
※1/2すれば、簡単に３角形の面積が求まります。
両ベクトルに垂直
(向きはaをbに小さな角度で重ねる向きにネジを回転させたときに進む方向、θ＝０ならそもそも外積も０なので向きは気にせず)

という特性を持ちます。たとえば、頂点が定義された三角形の法線ベクトルが必要な場合(案外よくある)、頂点間で方向ベクトルをつくって、その外積を求めて、長さで割る(長さの逆数をかける)(normalize)と得られます。ちなみに、CG分野ではそれを前提に、頂点を定義する順番で表裏の区別をつけます。
ちなみに(2)、右ネジの進む方向がわからなくなったら、右手を握って親指を立ててみてください。人指し指〜小指の指す回転方向にネジをまわすと、親指の方向に進みます (フレミングといっしょで手を間違ったらアウト(笑))。

ベクトルの微分
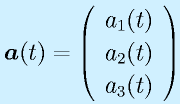
$\vect{a}(t)=\left(\begin{array}{c}a_1(t)\\a_2(t)\\a_3(t)\end{array}\right)$
に対して、
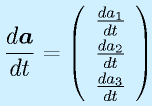
$\frac{d\vect{a}}{dt}=\left(\begin{array}{c}\frac{da_1}{dt}\\\frac{da_2}{dt}\\\frac{da_3}{dt}\end{array}\right)$
のように、単純に成分ごとに微分する。その他の公式類は線形代数の教科書を引っ張り出して勉強しておくこと。

行列

行列：
例)
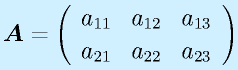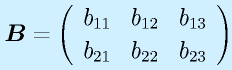
$\vect{A}=\left(\begin{array}{rrr} a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\end{array}\right)$ 、 $\vect{B}=\left(\begin{array}{rrr} b_{11}&b_{12}&b_{13}\\b_{21}&b_{22}&b_{23}\end{array}\right)$
(２×３)

行列は数字や関数を縦ｍ行×横ｎ列の形に並べたものです。一般に大文字、ボールド表記。特にｍ＝ｎの場合、ｎ次正方行列といいます。ベクトルは行列の特殊な例(ｎ×１、１×ｍ)とも見ることができます(行列とベクトルの演算は行列同士の演算として扱える)。
各成分を個別に扱うときには $a_{ij}$ の形で第ｉ行第ｊ列を表します(小文字、非ボールド、添字)。

用途：
行列は、座標変換(回転)や関節の角度とロボットの姿勢の関係を表すなどに使用されます。

行列の基本演算：
行列の和は行の数および列の数が等しい行列間のみで定義できます。
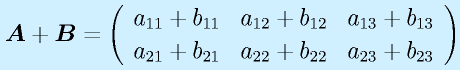
$\vect{A}+\vect{B}=\left(\begin{array}{rrr} a_{11}+b_{11}&a_{12}+b_{12}&a_{13}+b_{13}\\a_{21}+b_{21}&a_{22}+b_{22}&a_{23}+b_{23}\end{array}\right)$

スカラ倍は各要素がスカラ倍になります。
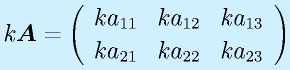
$k\vect{A}=\left(\begin{array}{rrr} ka_{11}&ka_{12}&ka_{13}\\ka_{21}&ka_{22}&ka_{23}\end{array}\right)$

行列の積：
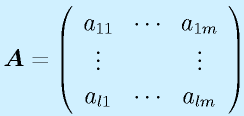
行列の積は、行列がｌ×ｍとｍ×ｎの形と、一つ目の行と二つ目の列の数が一致するときのみ定義でき、ｌ×ｎの行列が出来ます(もちろん l=m=n という場合もあり)。 $\vect{A}=\left(\begin{array}{ccc} a_{11}&\cdots&a_{1m}\\ \vdots&&\vdots \\a_{l1}&\cdots&a_{lm}\end{array}\right)$
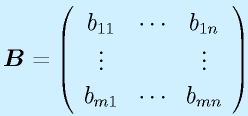
$\vect{B}=\left(\begin{array}{ccc} b_{11}&\cdots&b_{1n}\\ \vdots&&\vdots \\b_{m1}&\cdots&b_{mn}\end{array}\right)$
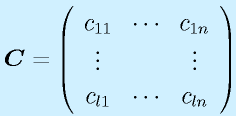
$\vect{C}=\left(\begin{array}{ccc} c_{11}&\cdots&c_{1n}\\ \vdots&&\vdots \\c_{l1}&\cdots&c_{ln}\end{array}\right)$
$\vect{C}=\vect{A}\vect{B}, c_{ij}=a_{i1}b_{1j}+\cdots+a_{im}b_{mj}$
定義は上式のようになりますが、覚えるときは以下のようなイメージで覚えると分かりやすいかもしれません。
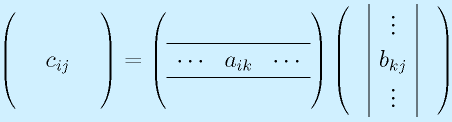
$\left(\begin{array}{ccc} 　&　&　\\ &c_{ij}& \\ &　&\end{array}\right) = \left(\begin{array}{ccc} &&\\\hline \cdots&a_{ik}&\cdots\\\hline &&\end{array}\right) \left(\begin{array}{c|c|c} 　&\vdots&　\\ &b_{kj}&\\ &\vdots&\end{array}\right)$

注意：
一般に、
$\vect{AB}=\vect{BA}は成立しない$
ことに注意。そのため、行列の乗算を行うときは、「右からかける」「左からかける」と掛け方に注意します。
例)
$\vect{A}&=&\vect{B}$ に対して
左からCをかけた $\vect{CA}=\vect{CB}$ と、右からCをかけた $\vect{AC}=\vect{BC}$ は成立しますが、
左右をごちゃまぜした $\vect{AC}=\vect{CB}$ は一般に成立しません。

行列によるベクトルの変換：
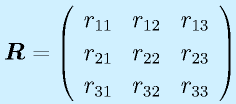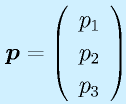
$\vect{R}=\left(\begin{array}{rrr} r_{11}&r_{12}&r_{13}\\r_{21}&r_{22}&r_{23}\\r_{31}&r_{32}&r_{33}\end{array}\right)$ 、 $\vect{p}=\left(\begin{array}{r} p_1\\p_2\\p_3 \end{array}\right)$
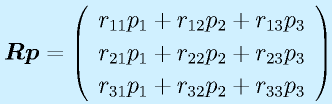
$\vect{R}\vect{p}=\left(\begin{array}{r} r_{11}p_1+r_{12}p_2+r_{13}p_3\\r_{21}p_1+r_{22}p_2+r_{23}p_3\\r_{31}p_1+r_{32}p_2+r_{33}p_3\end{array}\right)$
たとえば、３次のベクトルに左から３×３の行列をかけると、再び３次のベクトルになります。これは、座標系の回転など、あるベクトルを何らかの規則で変換する場合につかえます。

転置：
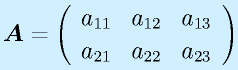
$\vect{A}=\left(\begin{array}{rrr} a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\end{array}\right)$
に対して、
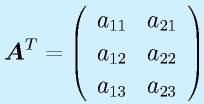
$\vect{A}^T=\left(\begin{array}{rr} a_{11}&a_{21}\\ a_{12}&a_{22}\\ a_{13}&a_{23}\end{array}\right)$
と行と列を入れ替えたものを転置と言い、右肩に添字Ｔをつけて表します。
("Tenchi"のTではなく、"Transpose"のT)
空間的にはあまり意味のある操作ではありませんが、数学的処理においてつかうことがあります。

逆行列：
ｎ次正方行列(ｎ×ｎの行列)Ａに対して、
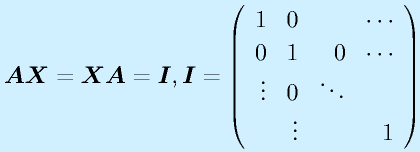
$\vect{AX}=\vect{XA}=\vect{I}, \vect{I}=\left(\begin{array}{rrrr}1&0&&\cdots \\ 0& 1 & 0 & \cdots \\ \vdots &0 &\ddots&\\ &\vdots& & 1 \end{array}\right)$
(行列Ｉは対角成分のみ1で残りは0のｎ次正方行列、単位行列)
となるようなｎ次正方行列Ｘを、Ａの逆行列といい、 $\vect{A}^{-1}$ と右肩に"-1"をつけて表します。逆行列は必ず存在するとはかぎりません(行列式が０でない場合に存在)。

行列式および逆行列の計算法に関しては、時々必要になるので各自線形代数学の教科書で確認して、２×２、３×３の行列に関しては求められるようにしておいてください。

逆行列は、ロボット工学においては、「逆変換」の意味で用いられます。ある座標系から別の座標系に行列Ｒで変換できる場合に、Ｒの逆行列を用いると逆の座標変換ができます。

つかう数学

心　得

基礎、代数

基礎の基礎

三角関数

微分

線形代数

ベクトル

行列

補　足

つかう数学

心 得

基礎、代数

基礎の基礎

三角関数

微分

線形代数

ベクトル

行列

補 足

心　得

補　足