プチテスト＆レポート 2010

最終更新： 2011/02/10 18:50:11

傾向と対策？

プチテストは本講義を進め、修了するにあたり、できないと困るというレベルのごく単純な計算を基本に出題しています。ということは、このくらいはできないと合格の可能性も著しく低下するわけで、興味のみで単位抜きに受講している学生さんは別として、必ず計算できるようにしておいてください。できるからと言って合格は保証しませんが、できないときついです。

レポートに関しては、多少まじめに計算しないと大変そうなネタを提供します。

プチテストとその解答例

第１回 9/13

Ｑ１：
$\Mss123456789\Mss101010001$
を計算せよ。
Ｑ２：
$\vect{a}=(1~~2~~3)^T,~~\vect{b}=(4~~5~~6)^T$
のとき
$\vect{a}\cdot\vect{b},~~\vect{a}\times\vect{b},~~\vect{b}\times\vect{a}$
を求めよ。

Ａ１：
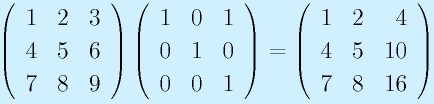
$\Mss123456789\Mss101010001=\Mss12445{10}78{16}$
Ａ２：
$\vect{a}\cdot\vect{b}=4+10+18=32$
$\vect{a}\times\vect{b}=(2\times6-5\times3~~3\times4-6\times1~~1\times5-4\times2)=(-3~~6~~-3)$
$\vect{b}\times\vect{a}=(5\times3-2\times6~~6\times1-3\times4~~4\times2-1\times5)=(3~~-6~~3)$

ただ計算するだけ。a×b=-b×a, ともにa,bとの内積が０となることに注意。
"-3i+6j-3k" の解答もオマケでＯＫとしたが、ここではijkが定義されていないので、解答としては不完全。「各軸の単位ベクトルをi,j,kとする」と付記してあれば、問題ない。

第２回 10/25

Ｑ：
Ｒ＝"60度回転"のとき、Ｒ²が"120度回転"になることを確認せよ。

Ａ：
60度＝π/3、120度＝2π/3
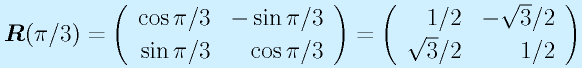
$\vect{R}(\pi/3)=\Mtt{\cos \pi/3}{-\sin \pi/3}{\sin \pi/3}{\cos \pi/3}=\Mtt{1/2}{-\sqrt3/2}{\sqrt3/2}{1/2}$
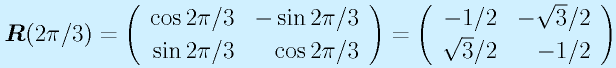
$\vect{R}(2\pi/3)=\Mtt{\cos 2\pi/3}{-\sin 2\pi/3}{\sin 2\pi/3}{\cos 2\pi/3}=\Mtt{-1/2}{-\sqrt3/2}{\sqrt3/2}{-1/2}$
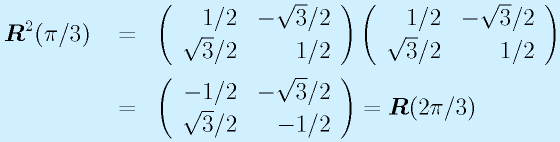
$\vect{R}^2(\pi/3)~&=&\Mtt{1/2}{-\sqrt3/2}{\sqrt3/2}{1/2}\Mtt{1/2}{-\sqrt3/2}{\sqrt3/2}{1/2}\nonumber\\&=&\Mtt{-1/2}{-\sqrt3/2}{\sqrt3/2}{-1/2}=\vect{R}(2\pi/3)$
よって、Ｒ²は120度回転となる。

第３回 11/15

Ｑ：

凹
｜
○
｜
○
｜
○
｜
◇
｜
￣

なる構造のロボットを立体的な絵(イラスト)で書いてみよ。また、できる作業を考えて例示せよ。

Ａ：
土木工事のショベルカーなどはこの一例。根本の関節で旋回、つぎの２関節で手先位置、最後の１関節でバケット角度など。
実際にあった解答例：
物体搬送、花に水をやる（エンドエフェクタがカップに見えた？）、ショベルカー、宝物をまもる
誤答例：
クレーン＝クレーンは途中が直動関節。

おもに
・基部で360度旋回できること
・手先の位置と方向(手先を平行/水平なまま動かせる)が指定できる
ことが重視されているようです。

減点例：
パワーショベルの旋回軸が書いていない、そもそも構造が違う、腕が枝分かれしまくって蛇足など。
関節が多い/少ない、イラストでどこが曲がるかが全くわからない。
自由度の順序を逆にするのも題意からすると飛躍しすぎ。
絵心は不問。ただし、「伝えようとしたイラスト」でない場合は、不足具合に応じて減点。

第４回 12/20

Ｑ：
車輪直径 2r=100mm、車輪間隔 2d=200mm の対向２輪型ロボットにおいて、一定角速度で右車輪がπ、左車輪が３π前進方向に回転した。ロボットの移動軌跡を図示せよ。

Ａ：
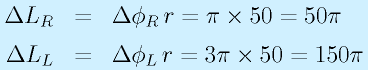
$\Delta L_R&=&\Delta\phi_R\,r=\pi\times50=50\pi\nonumber\\ \Delta L_L&=&\Delta\phi_L\,r=3\pi\times50=150\pi$
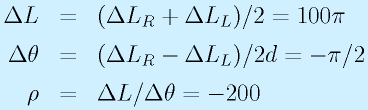
$\Delta L&=&(\Delta L_R+\Delta L_L)/2=100\pi \nonumber\\ \Delta \theta&=&(\Delta L_R-\Delta L_L)/2d=-\pi/2 \nonumber\\ \rho&=&\Delta L/\Delta \theta=-200$
よって、ロボットは半径200mmでπ/2旋回する。これを適宜図示すればよい。
ただし、θとρにマイナスがついていることが要注意。これは元の式を立てた図に対して、逆回転、逆方向に旋回中心があることを意味する。単純に左車輪がより回っていることをよく考えれば当然。

解答をみて気づいたこと：
例年出題している問題で、いつもは上記計算が出来ていますが、そのあとの図示がちゃんとできていません。
ロボットに限らず、機械分野では計算結果や設計結果を正しく思い浮かべることが重要です。今回の結果を図式化するにあたって考慮すべき点は

ロボットの旋回半径は200mmで、これは「車輪間隔に等しい幅」であること
ロボットの旋回角はπ/2＝90度、直角であること。

の２点です。皆さんの書いた図で多かった例は、９０度は出来ていても、半径と車輪間隔の関係がいい加減というものでした。また、旋回を扇形で示し、その角度が３０度もないのに、そこにπ/2と記載するケースもそこそこありました。車輪移動ロボットの場合、どの辺りを中心に回るかで障害物に当る当らないなどの影響が出るため、きっちりイメージすることが望まれます。

レポート

※レポートは未提出者がいるため、直接の回答は掲載しない。

第１回（10/11/8出題、10/11/22 講義開始時に回収)

Ｑ：
講義で行った「オイラー角の解析」と同様に、
　　Ｘ軸まわりにφ→Ｚ軸にθ→Ｙ軸にψ
回転するオイラー角回転変換の変換行列
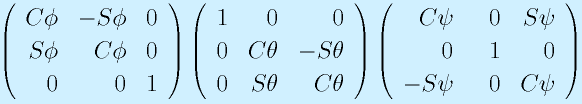
$\Mss{\Cph}{-\Sph}{0}{\Sph}{\Cph}0001 \Mss1000{\Cth}{-\Sth}0{\Sth}{\Cth} \Mss{\Cps}{~~0}{\Sps}010{-\Sps}0{\Cps}$
を求めよ。

また、Rが与えられたときに、(φ,θ,ψ)を求める方法を検討せよ。

ヒント：
頑張って計算する。計算結果は、各列ベクトルの大きさが１、各列ベクトル間の内積が０となることでほぼ検算できる(ならないときは計算ミス)。

レポートは指定の用紙で提出すること。用紙が必要な場合は熊谷まで申し出ること
※また、用紙をぐちゃにしないこと。レポート類はコンピュータで処理しています。

第２回（10/12/20 出題、11/01/17 講義開始時に回収）

　対向２輪型のロボットを作り、走行試験を行ったところ、機体ごとに以下のような不具合が生じた。各事例ごとに、考え得る原因を列挙し、具体的な式、数値、図などとともに述べよ。

直進の指示をモータに送ったが、実際には半径10,000[mm]の円弧を描き右にそれた。
直進は正常であったが、90[deg]のその場旋回(ρ=0)を指示をしたところ、92[deg]回ってしまった。
1,000[mm]の直進を指示したところ、ほぼ1,000[mm]前方に移動したが、右に10[mm]だけずれていた。
しかし、ロボットの向いている方向(講義でのθ)は移動の前後で同一であった。

各々、考え得る可能性は多岐にわたるため、本紙両面の範囲で、可能性が高いと思われる順に最大でも三つ程度を記述せよ。なお、必要なら、2r=100[mm]、2d=200[mm]を使用せよ。

熊谷正朗 [→連絡]
東北学院大学工学部機械知能工学科 RDE

［｜　］