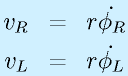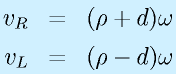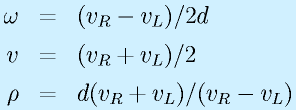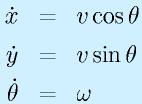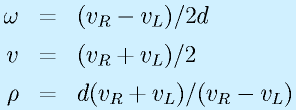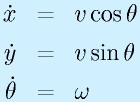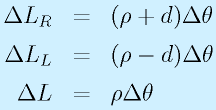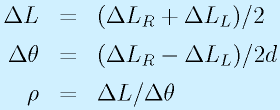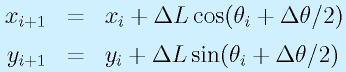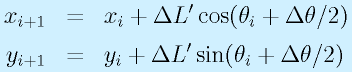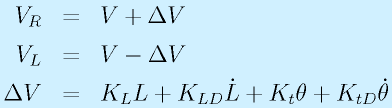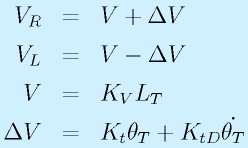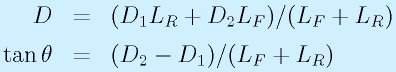ここでは移動ロボットの大部分が採用している移動機構である車輪について、扱います。
最近はちらほらと脚移動が見えるようになってきましたが、依然として移動ロボットの大部分は車輪移動であり、平坦地での移動に限れば今後も脚にとってかわられることはないと考えられます。
車輪移動の場合、最低限2個のモータの回転を制御すれば平面を自由に走り回ることができ、また停止しているときに必要なエネルギーは斜面でなければ微々たるものです。
制御回路をちょっと工夫すれば、減速時に走行の運動エネルギーのある程度を電気エネルギーとして回収することも可能であるなど、効率にも優れます。
ところが、特殊な例を除いて、車輪移動は移動方向に大きな制限があります。
自動車や自転車は前後には走りますし、カーブして走行もできますが、真横には移動できません。
そのため、真横に移動するには切返などが必要です。
これは制御上もやっかいな問題になり得ます。
そのようなわけで、移動ロボットの代表例として、車輪移動の基礎を学びます。
前提「車輪は滑らない」
車輪による移動には様々な利点がありますが、その一つにはそこそこの範囲をそこそこ正確に移動できる、もしくは移動した経路をそこそこ正確に算出できるというものがあり、このページでも後にその方法について扱います。
その際に大きな前提となることが「車輪が滑らない」ということです。車輪移動ロボットの数学は、この前提の上に成り立っています。
つまりドリフト走行は禁止です。以下では、車輪が滑らないことを前提にします。
車輪移動
車輪による移動は、ロボットを支えている車輪が適当に転がることによって行われます(当然?)。
ここで重要なことはすべての車輪が「滑らない」という条件です。
車輪が滑らないという前提では次のようなことが言えます。
- 車輪は車軸に垂直な方向にしか移動できない。車軸方向には移動できない。
(だから縦列駐車はたいへん、どうしても横に移動したいときはドリフトなど)
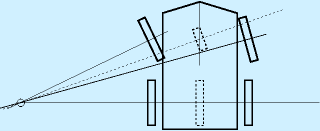
- 車両が運動しているとき、各瞬間ごとにどこかに「旋回中心」という点が存在して、すべて車輪の回転軸はこの点を通る。
この瞬間には、各車輪、ロボットは旋回中心を中心とする円運動を行う。
(車軸が傾いている場合を考えると、旋回中心を通り、ロボットの運動面に垂直な線と、車軸が交差する)
前者は当たり前として、後者の「すべての車輪は旋回中心と結んだ線に垂直な方向に運動」ということを頭に入れておくと、ロボットの挙動が理解しやすくなります。また、この瞬間的な円運動の半径を回転半径(一般的な表現では曲率半径)といいます。
以下では単純で代表的な2種類のロボット形態を示します。
対向2輪型(2輪駆動1キャスタ)
多くの車輪移動型のロボットが採用するのがこの形態です。
2個の車輪を左右対称にロボットに取り付け、それぞれを独立に駆動します。
2輪だけではシーソーのように倒れてしまうため、補助的にキャスタやボールキャスタをとりつけます(蘊蓄は下の補遺参照)。
この方式が広く使われているのは、
- 作るのが簡単。
一番単純にはモータ(ただし高トルク)に車輪をつけて2個並べておしまい。
減速系が必要な場合も2個つくって対称に配置すればいいことが多いです。
- 数学が簡単。
高校生でもたぶんあっさり理解できます。
また軌道計画が容易です。
- 旋回半径の設定が容易。自由度高。
左右の車輪の回転方向を逆、回転速度をいっしょにすると、両車輪の中点を中心に旋回することもできます。
旋回半径は左右の車輪の回転速度の差で決まります。また、旋回中心は両輪の軸上のどこかにあります(軸をずらすことはできない、ずらす必要性もないけど)。
そのようなわけで、移動ロボットでは非常に多くつかわれています。
ロボットの制御は両輪の回転で行います。
ステアリング型(1輪駆動1ステアリング)
対向2輪が駆動を2系統持っていたのに対して、駆動を1系統にしてかつ、ステアリング機構を持たせたものがこのタイプです。
数学的には、(傾けないでのる)2輪車や、4輪の自動車(4WDS除く、ステアリング2輪)も、この形態として扱うことができます。
対向2輪型は、2個ついている駆動装置がどちらも走行に使われるため、同じようにパワーが必要です。
それに対して、このタイプは駆動のための動力と、操舵のための動力を分離しているため、小回りより出力重視な場合に効果的です。
自動車がそのいい例です。エンジンで作り出した動力で駆動する一方で、ステアリングを動かすこと走行方向を決めます。
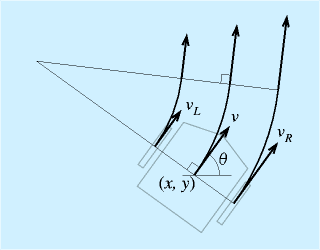
右の図で一番上は、基本的な構成です。後輪2輪は車体を支えるためだけに自由に回るように取り付け、前輪の方向(ψ)を決めて、車輪を回転させて移動します。ただし、この場合、駆動機構をコンパクトに納めるのがたいへんなので、前輪の回転は自由に、後輪の一方を駆動輪にする場合もあります。
駆動のアンバランスを避けるためには、ディファレンシャルギアを搭載して両輪を駆動しますが、移動ロボットでそこまでやることはあまりみられません。
旋回中心は後輪の軸と前輪の軸が交わったところにできます。
二つ目は2輪にしてしまった構成です。数学的には、3輪と解釈されるよりも、この2輪モデルがよく使われるようです。
三つ目の図はよくある自動車の構成です。4輪にして前輪2個に操舵機構を設けます。
ここで注意することは、すべての車輪の軸が旋回中心で交わるために、前輪の操舵角が左右で異なることです。
内側の車輪がよりきつく曲がります。こうしないと滑りが発生するわけです。
そのため、自動車の場合は特殊なリンク機構(アッカーマンステアリング機構)などでこの関係が成り立つようにします。
また、向きは同じですが、この状態では後輪は左右で回転数が異なります。
内側に比べて外側の車輪が多く回転する必要があります。
ロボットならモータを独立につけることもありますが、自動車の場合にはエンジンは一個なので(電気自動車は別)、ディファレンシャルギア(デフ)でその回転数差を作り出します。デフは「入力の角速度×2=右の角速度+左の角速度」となる機構で、平均速度はそのままに差を作り出します。
もちろん、前輪駆動の場合も左右に回転数差があるので、デフは必要です
(蛇足:4輪駆動だと、前後各々の平均の間にも差があるので前後間にセンターデフが必要)
この節ではロボットのモデルを数学的に解釈します。
上で大きく2種類のロボットがあるとしましたが、ここでは扱いやすい対向2輪型を解析します。
対向2輪ロボットの数学
ロボットの操作量は、一般に車輪の回転速度です。
トルクや位置制御をする場合もありますが、とりあえず速度で解析します(位置の場合は自己位置推定で詳述)。
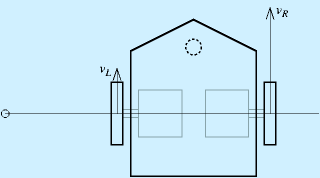
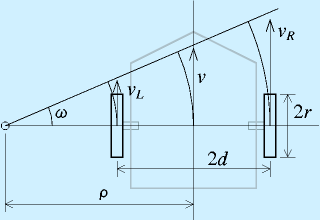
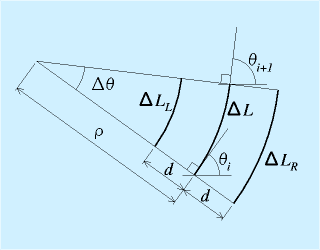
左右各々の車輪の回転角度をφR、φLとすると、車輪の接地点での速度vR, vLは、車輪の半径をrとして
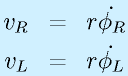
で得られます。
ここで、旋回中心回りの運動を考えます。
ロボットの旋回角速度をω、ロボット中心の速度をv、旋回半径をρとすると、

一方、中心から車輪までの距離をdとすると、それぞれの車輪の旋回半径はdだけ増減するため、
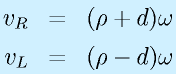
となります。この式を解いて
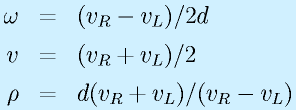
が得られます(ただしρの正方向は進行方向左、右に中心がある場合は負になる)。
vR=vL、両輪が同じ速度で回転する場合は旋回半径ρが無限大となります。
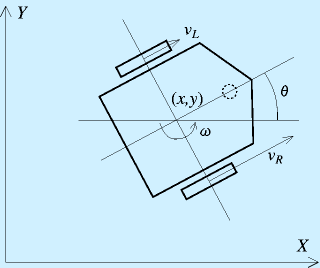
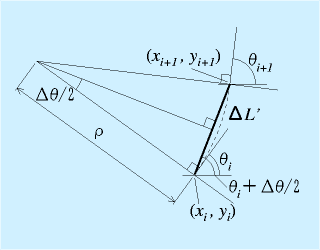
ロボットを外部の座標系で見た場合は
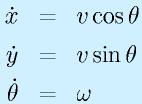
となり、ロボットの運動が両輪の回転角速度をもとに記述できることが確認できました。
対向2輪ロボットの動作例
上の数式を元に&次にやる自己位置推定の計算手法をもとに、ロボットの動きを画像・映像にしてみました。
図中、オレンジおよび黄色の矢印は車輪の速度、車輪についた赤の三角は車輪の回転を確認するための目印です。車体中央にあったり、そこから延びる赤紫の小円と棒はその時点での旋回中心、回転半径を示しています(ただし、半径無限大のときは半径0表示)。
一つ目の例では両輪を同じ速度で加減速させています。
両輪に速度差がないので、真っ直ぐに走ります(旋回半径は無限大)。
二つ目の例では左右に一定の比率の速度差をつけています。
具体的には、右は左の約3倍(10:3)の速度です(後半は逆に1:2)。
上の回転半径の式より、d(10+3)/(10-3)でだいたい2dくらいになります。
また、速度比が一定なので、中心位置は変わりません。
映像だけの三つ目では、より複雑に車輪を加減速しています。
旋回半径が伸び縮みすることが見えますし、左右が逆回転する際には両輪の間に入っています。
このように小回りや複雑な運動をしやすいことが対向2輪型の特徴です。
参考:
映像のパラメータ
| 車輪径(2r) | 100mm |
| 車輪間隔(2d) | 190mm |
| 数値解析間隔 | 1/30秒 |
| 床面格子間隔 | 200mm |
| |
直線走行、ワールド系、320x240 (2018/04/17, 224,725 bytes)
直線走行、ロボット追跡系、320x240 (2018/04/17, 304,725 bytes)
円弧走行、ワールド系、320x240 (2018/04/17, 285,525 bytes)
円弧走行、ロボット追跡系、320x240 (2018/04/17, 439,125 bytes)
複合走行、ワールド系、320x240 (2018/04/17, 304,725 bytes)
複合走行、ワールド系、640x480 (2018/04/17, 1,251,925 bytes)
複合走行、ロボット追跡系、320x240 (2018/04/17, 439,125 bytes)
※ワールド系:カメラをワールド座標に固定。ロボット追跡系:ロボットの位置を基準に移動カメラを設置、ただしカメラの姿勢は固定。
ここでは車輪移動ロボットの制御のうち、代表的な「経路に沿って走行」という手法を紹介します。
上述の対向2輪型ロボットは両輪の回転を制御することで様々な運動ができます。
その中で、人間が直接操縦するのではなく、自律的な用途のうちで、主なものを考えると
- 現在地点から目標地点まで移動
- 前方のターゲットを追跡
- 目標地点はわからないけどガイドラインに沿って移動
などがありそうです。
このうち、上二つは目標までの距離が異なるだけで、似た用途に思えます。
一方、上二つと三つ目は異なるように見えます。
しかし、実際にロボットを作った場合には、目標まで一直線に行くことができないケースもあり、多くのロボットはまずどこ(目標軌道)を通っていくかを決め(経路計画)、ついでその経路をたどるという方法をとります。
経路上に障害が現れた場合は、停止して待ったり、回避したりしますが、回避する場合は新しく経路を作り直す場合もありますし、計画済みの軌道からいったんはずれて復帰する軌道を取ることもあります。
いずれにせよ、「たどる」という動作が頻繁につかわれます。
そこで、ここでは「たどる」こと、ライントレースを紹介します。
ロボットを走行させる場合には、いくつかの方法があります。
- 目標軌道が与えられている場合、その軌道をもとに車輪の回転量をあらかじめ算出してその通りに車輪を動かす(フィードフォワード的)。
なめらかで最適な経路を取りやすいものの、車輪の回転ずれなどで経路がずれたことが「わかった」としても、修正のしようがない。
※ 車輪の滑りが原因の場合は「わからない」のでいずれにせよどうしようもないが、車輪の制御遅れなどの場合は「わかる」ずれが生じる。
- 目標となるものを時々刻々と検出しながら、目的に「あうように」車輪を回転させる。
フィードバック制御であり、安定になるように設計すれば、ずれなどに対して強い。また、目標がロボット外部にある場合、車輪が滑った分も補正できる。
※ 具体的に数式でずれを評価することで「あうように」しむける
- 自己位置推定で算出した現在座標、姿勢と、仮想的に設定した目標ラインを比較し走行する。
車輪の滑りがなければ、なめらかである程度正確な走行がしやすい。
上記外部を検出する手法はセンサの性能や情報取得間隔などによってガタガタになることがある。
以下では代表的な?アイデアを紹介します。
仮想的なラインに追従
 コンピュータの中に仮想的なラインを設定して、自己位置推定で得たロボットの位置と姿勢角度を仮想的なラインと比較し、ロボットを目標軌道に載せる方法です。
コンピュータの中に仮想的なラインを設定して、自己位置推定で得たロボットの位置と姿勢角度を仮想的なラインと比較し、ロボットを目標軌道に載せる方法です。
この方法でも非常に多くの手法が提案されていますが、主に考慮されることは以下の二つです。
- ロボットと目標線の距離が0であること。
(線上をトレースする場合)
- ロボットの進行方向と、線の接線方向が一致すること。
これを満たすように、両車輪の回転速度を調整します。
(調整の仕方が千差万別)
例をあげます。
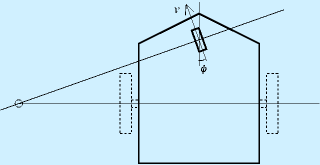
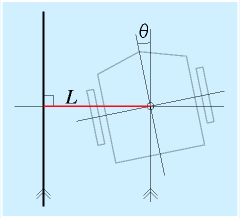
右図に示すように、ロボットの中心から軌道までの距離をL、軌道の接線方向とロボットの進行方向の成す角をθとします。
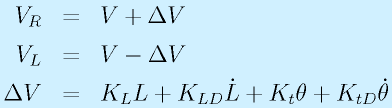
ここでK?は定数で、適宜設定します。
V は平均移動速度で、両輪の速度差ΔVでロボットの旋回成分を操作して走行します。
KLおよびKtの項はLとθがゼロになるようにするためのものです。
Lがゼロでないときは、ロボットの進行方向を線の向きに向ける必要があります。
KLDおよびKtDの項はLとθの速度を制御します。
例えば、ロボットが線に近づいてLが十分小さくなってきたとしても、ロボットが勢い良く線に近づいている場合(つまりθが大きいわけですが)にロボットの進行方向を変える必要があります。
パラメータが4つあって決めるのに困りそうですが、実はやってみると案外後半のθの項がなくてもそこそこ動くようです。
KLDとKtが似た性質を持っていることもあると考えられます。
また、極端にはKL以外が0でも使えることがあります。ただしこの場合は線を挟んでロボットが左右に蛇行することになり、スムーズに走らせるには微分項も含める必要があります。
この方法の難点は軌道の定義方法です。直線や円弧のような軌道であれば、Lを求めることは容易なのですが、複雑な軌道を作ろうとすると、どこが最近点なのかを求めることが難しくなります。
仮想的なターゲット追尾
 上の方法の問題点は軌道とロボットの位置関係を求めることがやっかいなことです。
その一つの解決案として、目標軌道の上で仮想的な(実質的な)ターゲットを目標速度で移動させ、ロボットはそれに追従するように仕向ける方法が考えられます。
上の方法の問題点は軌道とロボットの位置関係を求めることがやっかいなことです。
その一つの解決案として、目標軌道の上で仮想的な(実質的な)ターゲットを目標速度で移動させ、ロボットはそれに追従するように仕向ける方法が考えられます。
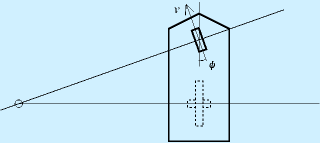
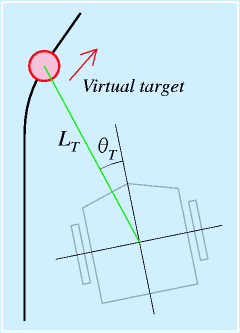
まず、自己位置推定で得たロボットの位置と姿勢をもとに、移動する仮想ターゲットの位置をロボットの座標系上に変換します。
すると、ロボットから見て、ターゲットの位置を距離LTと方向θTで表せます。
これを元に、例えば
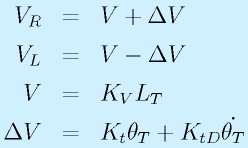
とします。
この式の意味するところは、「平均的な車両速度はターゲットとの距離に比例」「車両の方向がターゲットの方向を向くように姿勢を回転させる」です。
ロボットの頭にゴム紐をつけて引っ張るようなイメージです。
この方法はターゲットさえ移動させればいいので、かなり扱いやすい方法です。
また、ターゲットは仮想的なものである必要はないので、目標追尾型の動作にそのまま使えます。
ただし、原理的にはロボットがターゲットにたどり着くことはないので(そのまえにLTが小さくなることで速度が小さくなってしまう)、目標地点までターゲットを動かしただけでは目標にたどり着けないという問題点があります。
また、KV, Kt, KtDの各係数を大きくしすぎると制御が発散しかねませんが、小さくするとターゲットとロボットの間にすきまが開くため(よわいゴムひもで引っ張る感じ)、細かな経路計画をしてもおおざっぱにしかついてきません。
その結果、回りにぶつけたりすることがあり得ます。
実在のラインのトレース
 普通にライントレースロボットといったら、このタイプです。
路面にひかれたラインをセンサで読み取り、そのラインをたどるように走ります。
ラインは白い床に黒い線といった明暗で示す場合、金属箔のテープをはったり磁石を埋めたりする磁気的に示す場合などがあります。
普通にライントレースロボットといったら、このタイプです。
路面にひかれたラインをセンサで読み取り、そのラインをたどるように走ります。
ラインは白い床に黒い線といった明暗で示す場合、金属箔のテープをはったり磁石を埋めたりする磁気的に示す場合などがあります。
一番原始的には、ロボットの軸に対称に、左右にセンサを取り付け、左のセンサが反応したら右に進路変更、右のセンサが反応したら左に進路変更、という方法があります。
これはライントレースのキットやおもちゃでも使われるような方法で、このくらい単純でもそれなりに動作します。ただし、ロボットは頭を激しくふりながら前進します。
ふれを小さくするにはセンサの間隔をつめることが解決策の一つです。
ただ、その場合はラインからはずれる確率も高くなるので、センサの数も増やします。
また、センサの間隔をラインの幅よりも狭めることで、複数のセンサでラインを読むようにして、読みとばしを避けると同時に、センサの出力を平均化することでセンサの数以上の細かさを得ることができます。
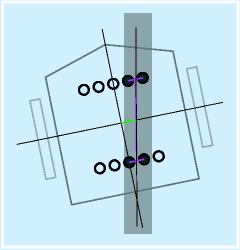
例えば、右の図で前方のセンサは右二つが線を踏んでいます。
5個のセンサにそれぞれ重みとして 2,1,0,-1,-2 を割り当てると、(-1*1-2*1)/(1+1)=-1.5 と計算できます。
2〜-2でセンサの数は5個ですが、1個か2個同時に踏む程度の間隔を設定すると、9段階の位置になります。
センサをオンオフだけではなく、アナログ的に処理するとさらに分解能をあげられます。
ふれを小さくするもう一つの方法はロボットの姿勢を反映することです。
最初に述べた方法のように、ロボットの姿勢をフィードバックします。
センサの数をけちる場合は、センサで読んだラインの位置の時間変化をフィードバックします(KLDに相当)。
センサを前後に並べることができる場合は、右図のように前後のセンサ群で検出したラインの位置から線の傾きを出し、それを反映させます(Kt項に相当)。
センサを倍つけなければならないようですが、このラインセンサによる方式ではセンサ群は車軸より前方にないとやっかいという性質があります(車軸から遠いほどなめらかに動く:原理を考えてみましょう)。
そのため、ロボットをバックさせるときは、後ろにもセンサがあったほうがいいわけです。
すると、車両の傾きを得るにも使えることになります。
この方法は工場での搬送車などに良く使われます。物理的なラインが存在するため、車輪の滑りなどにも強く、単純な制御方式(=信頼性を確保しやすい)で移動できるためです。
また、ラインセンサを流用すると停止線を読んだり、地面のバーコードを読み取って動作を変えたり様々な使い方ができます。
そのほか、高速道路での自動運転の研究でも、道路に磁石を埋めてそれを磁気センサで読み取る方式が進められています。
自動運転というとカメラを搭載して画像処理という方法がありがちですが、磁気センサの方が単純であるため、信頼性を確保しやすいといえます。
しかし、あまりに単純にこの方法をつかうと、センサの数が十分でないと動きががたがたしたり、精度が確保できなかったり、上二つの方法に比べて見た目は劣ります。
そこで、基本的には自己位置推定をベースに走行して、ラインを読みながらその補正を行う、という合成手法が使用される場合もあります。
壁伝い
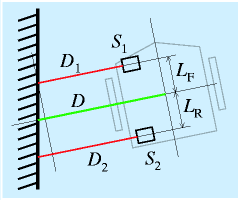 物理的な対象をたどるばあい、壁を伝うというケースもあります。
この場合、壁までの距離を測るセンサが必要になります。
ポピュラーなセンサとしては、超音波と光三角測量のセンサがあります。
物理的な対象をたどるばあい、壁を伝うというケースもあります。
この場合、壁までの距離を測るセンサが必要になります。
ポピュラーなセンサとしては、超音波と光三角測量のセンサがあります。
超音波センサは、超音波を飛ばしてから返ってくるまでの距離を測ります。
相手が音を反射する材質ならなんでもいいのですが、雑音、最悪の場合はロボット自身のギアの出す音でも誤動作する場合があり、比較的静かな環境で使う必要があります。
最近使いやすくなった方法に光を用いて三角測量を行うセンサがあります。
通称、PSDと呼ばれていますが、小型のセンサで、電源をつなぐだけで数十センチまでの距離をそれに対応する電圧で出力してくれます。
値段も含めて非常にお手軽なセンサですが、赤外線を使うため、赤外線が反射しにくい素材ではつかえません。
※ PSDは本来はそのセンサに使われている受光素子の名前
さて、距離が測れるセンサがあったとして、ロボットの側面に、前部と後部に一個ずつつけます。
一般には左右にそれぞれつけるので、4個になりますが、図では左側面だけ描きました。
このセンサで壁までの距離 D1、D2を測定します。
なお、光のセンサの場合は図に示すように真っ直ぐ測れますが、超音波の場合には広がりがでるので、真っ直ぐは測れません。
ただ、結果に悪影響をだすようなずれはあまりでません。
このとき、これまで同様に考えると、
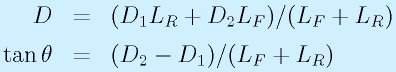
というように、壁までのロボットの距離と、壁との傾きがわかります。
一般には、Dが目的の距離D0になるように、(D-D0)がゼロになるように制御します。
この方法は壁までの距離を測ることができればよく、壁への衝突回避能力もついてくるのでお手軽です。ただし、壁がなめらかなところなら問題ないのですが、日本の一般的建築のように、壁がぼこぼこに入り組んでいる場合は距離が頻繁に変わって制御に失敗しやすくなります。
軌道の設定
紹介した4つの方法のうち、上二つは軌道を数式として事前に持っていることが前提です。
ロボットの軌道を計画する場合は、多くの場合はパラメトリックな線を使います。
例えば、円を表す場合、
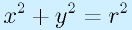
という書き方の他に

という書き方があります。
後者がパラメトリックな書き方で、媒介変数:パラメータであるtを変化させることで線ができます。
上で例示した仮想的なターゲットを一定速度で円弧上を動かすという場合は、後者の式でtを一定速度で変化させれば一発です。
それに対して、前者はそう簡単にはいきません。もちろん、yをxの関数で表す式を使うこともありますが、これは経路が基本的に真っ直ぐで、ちょっと脇にそれる程度の場合しかつかえません。
軌道を作る場合の数式も出るにもいくつかあります。
- 直線+円弧
分かりやすいケースで、数式も単純であるため、最近点が把握しやすくなります。
また、人間が経路を設定or検証する場合も直感的にわかりやすくなります。
ただし、一見連続的に見える線であっても、直線と円弧のつなぎ目では曲率半径が急に変わる=角速度が急に変わる=車輪の速度差が急に発生するため、そこで走行が乱れかねません。
- スプライン曲線
スプライン曲線は複数の点でその線が決定される、パラメトリックな曲線です。
スプライン曲線はいくつか種類がありますが、ポピュラーなものでは、すべての点を通過する曲線ができたりします。
便利ですが、線によってはすべての点を通すという制約がたたって、え?と思うような、波打った線が出てくることがあります。
- ベジェ曲線
最近のお絵書きソフトでも良く使われる、複数の制御点で決定されるパラメトリックな曲線です。
曲線の形は制御点で決まりますが、制御点をすべて通るわけではありません。
見た目、なめらかな線がわりと直感的に得られます。
制御点の数に応じて次数が定義されますが、各次数ごとに数式は決まっていて、制御点の座標だけを入れればパラメトリックな曲線式になります。
難点は、制御点でつくった折れ線の内側をなめらかにつなぐような感じの線がでるため、角すれすれとかを狙うと危険です。
- クロソイド曲線
走行距離に比例して、曲率(=1/曲率半径)が変化する曲線です。対向2輪で
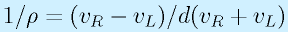
なので、一定速度(vR+vL=const)で走行する場合は、分子のvR,vLの変化速度が一定となることになり、なめらかな加減速が行われます。
詳細は扱いませんでしたが、ステアリング型の場合も操舵角が曲率に比例するため、一定の速度で操舵すればよい曲線です。
そのため、高速度道路本体や、インターチェンジのランプ道路の曲線として使用されています(一定速度で走っていれば、一定速度でハンドルを切れば良い=運転楽)。
車両から見ると幸せな線ですが、始点と終点を与えれば式が決まるような方法がないため、設計は困難です。
そのため、リアルタイムに決定されるロボットの軌道として使用されることはほとんど見掛けません。
このなかで、スプラインとベジェ曲線は制御点をちょっと動かすと経路の形がかわるため、臨時の障害物回避などにも便利です。
以上のような式を用いて、始点から終点まで障害物を避けるような軌道を立案して、その線に沿って、自己位置推定をしながら走るようにすれば、ロボットはかなりいろいろな仕事が出来るようになります。
移動できるようになると、障害物を知るためのセンシングが重要になってきます。
それはまた次の機会に。