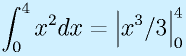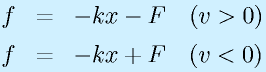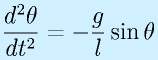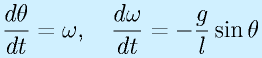数値計算系プログラム
[| ]
最終更新: 2011/02/10 19:35:08
このページについて
C言語でプログラムをつくるテーマとして、ここでは数値計算系をいくつか試してみます。
数値積分
簡単な数値積分
表計算ソフトのところですでにやったのと同じ計算を試みます。
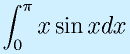
さしあたって、答えがπになることはわかっています。
// プログラム numint.c
#include <stdio.h>
#include <math.h>
int main(void)
{
int i,n;
double x,fx,d,u,dx,sum;
n=1000; // 分割数
d=0; // 積分の下限
u=M_PI; // 積分の上限
dx=(u-d)/n; // 分割の1区間
sum=0;
for(i=0;i<n;i++) // 分割数だけ回す
{
x=d+i*dx; // i番目の区間のx
fx=x*sin(x); // 積分する関数
sum=sum+fx*dx;
printf("%4d %8.5f %8.5f %8.5f\n",i,x,fx,sum);
}
printf("数値積分結果 %15.13f (解析解 %15.13f)\n",sum,M_PI);
return 0;
}
$ gcc -o numint numint.c
$ numint
0 0.00000 0.00000 0.00000
1 0.00314 0.00001 0.00000
2 0.00628 0.00004 0.00000
だ
ぁ
ぁ
998 3.13531 0.01970 3.14156
999 3.13845 0.00986 3.14159
数値積分結果 3.1415900697330 (解析解 3.1415926535898)
以下、プログラムの説明です。
- 計算そのものは
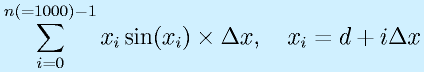
を求めています。変数sumに順次加えています。
- 積分範囲をd〜uにしています。
今回のように最初から目的が決まっている積分をするときは変数にする意味はさほどありませんが、何らかの目的で調整したり、他の計算にも使うことを考えて、あえて文字を割り当てています。
※こういうとき、「変」数ではなく「定」数として、文字を割り当てることも可能です。
※参考:const, #define
- 数値積分の間隔、Δx(変数名dx)は、d〜uを分割数nで割って決めています。
- 表計算では「想定していた計算の数だけ式をコピー」で計算回数を決めていましたが、プログラムは「何回」を最初から指定できるため、回数をまず決めて、それに応じてΔxを決めています。
- 計算するf(x)のxの場所は、d(i=0), d+dx(i=1), d+2dx(i=2),.. d+(n-1)dx(i=n-1, ループ最後)です。d+ndx=d+n(u-d)/n=d+u-d=u, つまり、最後はu-dxの場所になります。
- ループをn回回ったら、sumには合計が出ているので表示しています。
- あえて、M_PIをprintfで表示しているのは、比較用です。%fの指定を一致させておくと、比べやすくなります。
ちなみに、%fで表示させるdoubleの場合、小数点の上下合計(有効桁数)で15桁以上の数字は表示させても意味がありません(そもそもdoubleの扱える範囲)。
ここまで納得したら、以下の改造を加えてみましょう。
- さしあたり、n=1000を10,100,1000,10000,100000,と変えてみましょう。結果はどうかわりますか?
※表計算で実用的なのはn=1000相当程度、やれば10000もいけるが。プログラムはもっと増やせる。
- 途中経過の表示(1回目のprintf)は、なくても結果にはなにも影響しません。
むしろ、画面に表示するのが多すぎてうっとうしかったり、そもそも計算よりも表示のほうが時間がかかるのでトータルで時間が無駄だったりします。
printfの前に"//"をいれて消してしまいましょう。("//printf(...")
- けど、どこまで計算が進んだか、ある程度は表示してほしいという場合、
sum=sum+fx*dx;
printf("%4d %8.5f %8.5f %8.5f\n",i,x,fx,sum);
}
の部分を
sum=sum+fx*dx;
if(i%100==0)
{
printf("%4d %8.5f %8.5f %8.5f\n",i,x,fx,sum);
}
}
と変えてみましょう。
意味は「もし、iを100で割ったがゼロと等しければ」「printf」、です。つまり、i=0, i=100, i=200...の場合にprintfが実行されて表示が出ます。
結果、「100回に1回」表示されます。
当たり前ですが、この100を適当な数に変更すれば、まびき具合がかわります。
この手のプログラムは、ある程度計算量が多くなると瞬時には結果が返ってきませんが、「どこまですすんだか」がわからないのも精神衛生上芳しくありません。ので、こういう小細工を覚えておくといいでしょう。
蛇足:このprintfの"\n"を"\r"に変えて、nを大きくしてみると、おもしろいかもしれません。
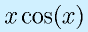 の積分を0〜πでしてみましょう。
の積分を0〜πでしてみましょう。
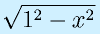 の積分を-1〜1でしてみましょう。
の積分を-1〜1でしてみましょう。
台形積分
 |
| 数値積分の誤差と計算方法 |
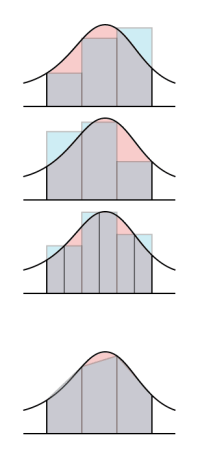
上の計算方法は、右図の一番上の図の水色(重なって灰色)の部分の面積の計算法です。
それに対して、一番下の図のように、台形をつないでいったほうが、より、形をきれいに表せそうです。この計算方法を台形積分といいます。
積分区間をN等分したとして、その区分点をx[0]〜x[N]とします。x[0]は積分区間の下限、x[N]は上限になります。また、その間隔をΔx(=(上限-下限)/N)とします。
(右図では、3等分してあって、x[0],x[1],x[2],x[3=N]に縦線が引いてある)。
また、x[i]に対する関数の値f(x[i])=f[i]と書くことにします。
上の、短冊を組み合わせた積分は、
![\sum_{i=0}^{N-1}f[i]\Delta x=\Delta x\sum_{i=0}^{N-1}f[i]](eqn/prognum.bhtml.eqn5.gif)
です(f(x[0])Δx+f(x[1])Δx+...)。
それに対して、台形でつくるときは、
![\sum_{i=0}^{N-1}\{f[i]+f[i+1]\}\Delta x/2=(\Delta x/2)\sum_{i=0}^{N-1}\{f[i]+f[i+1]\}](eqn/prognum.bhtml.eqn6.gif)
です。この、Σの中をよく見ると、
![(f[0]+f[1])+(f[1]+f[2])+(f[2]+f[3])+\cdots+(f[N-1]+f[N-1+1])](eqn/prognum.bhtml.eqn7.gif)
となっています。書き換えると、
![f[0]+2f[1]+2f[2]+\cdots+2f[N-1]+f[N]=f[0]+2\sum_{i=1}^{N-1}f[i]+f[N]](eqn/prognum.bhtml.eqn8.gif)
よって、元々の台形積分は、
![(\Delta x/2)\{f[0]+2\sum_{i=1}^{N-1}f[i]+f[N]\}=\Delta x\{\sum_{i=1}^{N-1}f[i]+(f[0]+f[N])/2\}](eqn/prognum.bhtml.eqn9.gif)
となります。先ほどの短冊を組み合わせた積分と見比べると計算に時間がかかりそうなひたすら合計する部分はほとんど変わらず(0...N-1が1...N-1になっただけ)、両端の1/2がくっついただけです。実質的に計算時間はほとんど変わりません。
ところが、この二つの積分は計算対象によっては劇的に精度に違いが出ます。
それを比較してみましょう。
台形積分は短冊の積分の結果に細工をすれば得られます。
![\Delta x\{\sum_{i=1}^{N-1}f[i]+(f[0]+f[N])/2\}&=&\Delta x\{\sum_{i=0}^{N-1}f[i]-f[0]+(f[0]+f[N])/2\}\nonumber\\&=&\Delta x\{\sum_{i=0}^{N-1}f[i]+(f[N]-f[0])/2\}](eqn/prognum.bhtml.eqn10.gif)
※Σに0を含めて、その分を外で-f[0]、計算まとめ
この式を別に解釈すると、短冊の時は、短冊の左端を目的の曲線にあわせるか、右端にあわせるかすることでもう一方の端の値が無視されるのに対して、両端を半分ずつ反映しましょう、とも見られます。
※上のプログラムをコピーし、numint_dai.cに名前変更、
※//★の行に注意して修正すると、手っ取り早い。
※もちろん、「慣れる」には打ち直すのがよい。
// numint_dai.c
#include <stdio.h>
#include <math.h>
#define f(x) ((x)*(x)) // ★追加
int main(void)
{
int i,n;
double x,fx,d,u,dx,sum;
n=1000; // 分割数 // ★1000に戻した?
d=0; // 積分の下限
u=4; // 積分の上限 // ★修正
dx=(u-d)/n; // 分割の1区間
sum=0; // sumはΣの値の計算
for(i=0;i<n;i++) // 分割数だけ回す
{
x=d+i*dx;
sum=sum+f(x); // ★式修正、printf削除
}
printf("解析解: %15.12f\n",(u*u*u-d*d*d)/3);
printf("数値積分(短冊):%15.12f\n",sum*dx);
printf("数値積分(台形):%15.12f\n",(sum+(f(u)-f(d))/2)*dx);
return 0; // ★↑3行:表示の修正
}
$ gcc -o numint_dai numint_dai.c
$ numint_dai
解析解: 21.333333333333
数値積分(短冊):21.301344000000
数値積分(台形):21.333344000000
$
プログラムはΣの部分をi=0〜n-1のforで繰り返しつつ求めたsumをもとに、最終的な計算はprintfに数値を渡す段階で行っています。
求めているのは
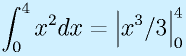
です。
ここで、新しいキーワードが増えました。
#define f(x) ((x)*(x))
これは、この先プログラム中に「f(?)」の形が出てきたとき、「((?)*(?))」に置き換えるように、という指示です。とりあえず、xが仮に書いてありますが、「x」の部分も書き換える、という意味しかありません。
これまでのプログラムでは積分したい関数は1回しか書かなかったので、直接書いていましたが、今回は台形積分の計算でもう2回使います。
関数を変えてみたいときに合計3回書き換えると面倒なだけではなく、書き間違いの可能性もあります。
そこで、f(?)と書くだけでいいようにしてしまいます。
その結果、「f(u)」は「((u)*(u))」に、「f(d)」は「((d)*(d))」にそれぞれ置き換えられます。
ちなみに、しつこく括弧が書いてあるには訳があります。
#define f(x) x*x → f(a)はa*a、 f(a+1)は a+1*a+1=2a+1
#define f(x) ((x)*(x)) → f(a)は((a)*(a))、f(a+1)は((a+1)*(a+1))
と、括弧がないと予期せぬ結果が起きやすくなります。
その側の括弧も、f(x)がx+3のような場合に重要になります。
括弧をつける癖をつけておきましょう。
なお、このdefineは
#define U 4
のように、()なしでも使え、その場合は U が出るたび、4に置き換えられます。
(UUには影響しません)
プログラムの上の方の u, d, n などはこの#defineで書くこともできます。
(ちなみに、見た目の区別のため、#define を使うときは、#defineを使った、という区別のため、大文字を使うことが一般です。それに従えばF(x)としたほうが無難です。)
もう、説明不要だと思いますが、 f(d)が上の式のf[0]、f(u)がf[N]にあたります。
試してみましょう
- 上のプログラムのまま、結果の精度の違いを見比べる。
- お約束でnを変えてみる。
- 積分範囲を0〜4から-4〜4にしてみる。
すると差が出ない。0〜4は単調増加の関数なのに対して、-4〜4にすると増減する。
増減する関数は短冊でも案外なんとかなる(不足とはみ出しが適当に帳消ししやすい)ため。
もっと端的には、この場合は f(d)=f(u)なので計算上一致するはず。
- 関数を変えてみる。
参考:
短冊と台形の違いは、f[i]と、計算に使うべき値を適当に減らしたことで無視されてしまった、f[i]〜f[i+1]の値を「どう推測したか」の違いでもあります。
短冊は0次関数(一定値)、台形は1次関数(直線)で考えたものです。この先、2次、3次と増やしていくとより精度は上がりますが、短冊と台形ほど近くはなく、計算も面倒になっていきます。
シミュレーション
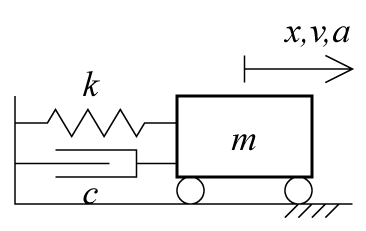 |
| バネとダンパによる振動 |
数値積分と同様に、シミュレーションもプログラムでつくれます。
ここでは、表計算ソフトで題材にした、バネとダンパ
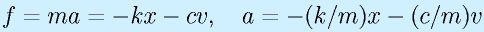
をもう一度やってみます。
// simu1.c
#include <stdio.h>
#include <math.h>
int main(void)
{
int i,n,nd;
double x,v,a,m,c,k;
double dt,end,iv;
m=1.0; // シミュレーション対象パラメータ
c=0.5;
k=1.0;
x=1.0; // xの初期値
v=0.0; // vの初期値
dt=0.001; // 計算区分
end=10; // 終了時間
iv=0.1; // 表示間隔
n=(int)(end/dt); // 計算繰返数
// "(int)"は「整数にする(切捨)」という指示。
nd=(int)(iv/dt); // 表示周期
for(i=0;i<n;i++) // 繰り返し
{
a=-(k/m)*x-(c/m)*v;
x = x+v*dt;
v = v+a*dt;
if(i%nd==0) // nd回に1回表示
{
printf("time:%6.3lf x:%6.3lf v:%6.3lf\n",i*dt,x,v);
}
}
return 0;
}
これまでのプログラムより、少し長くなっているように見えますが、準備部分が増えていて、forのループ部分はあまり変わりません。
実行すると、
$ gcc -o simu1 simu1.c
$ simu1
time: 0.000 x: 1.000 v:-0.001
time: 0.100 x: 0.995 v:-0.098
time: 0.200 x: 0.981 v:-0.190
time: 0.300 x: 0.957 v:-0.275
time: 0.400 x: 0.926 v:-0.354
time: 0.500 x: 0.887 v:-0.425
time: 0.600 x: 0.841 v:-0.489
:
time: 9.300 x:-0.079 v:-0.041
time: 9.400 x:-0.083 v:-0.031
time: 9.500 x:-0.086 v:-0.021
time: 9.600 x:-0.087 v:-0.012
time: 9.700 x:-0.088 v:-0.003
time: 9.800 x:-0.088 v: 0.006
time: 9.900 x:-0.087 v: 0.014
$
という結果が出てきます。
プログラムのポイントを以下に説明します。
- このプログラムの調整部分は、
m,c,k:シミュレーション対象の特性を指定
x,v:シミュレーション開始時の位置と速度を指定(初期条件)
dt:計算間隔Δtを指定
end:何秒経過後までを計算するかを指定
iv:何秒ごとに結果を表示するかを指定
です。
- 何回繰り返し計算するかは、end/dtで決まります(たとえば、0.1秒ごとの計算を5秒までするなら、5/0.1=50回)。これは小数(実数)の値ですが、「回数」は「整数」です。
そのため、「以下の値を整数とする」をいう意味を持つ「(int)(.....)」で、結果の変更をしてから、nに代入しています。
- 表計算では10000回程度の繰り返しが実用的には限度ですが、プログラムではより多くの繰り返し、別の見方では時間を細かく、より長い時間で計算できます。
しかしそれをすべて表示してしまうとあまりに細かくなりすぎるため、間引いて表示したほうが無難です。
間引くには、数値積分のところのテクニック、if(i%???==0) を使えます。
シミュレーション結果を表示する上では「○回に一回」よりは「○秒に一回」のほうが実用的です。そこで、それを「iv」で指定し、それが何回分かを「/dt」で計算しています。
- forループでは、aを求め、x,vの計算をしています。
(x,vの式の順序を入れ替えると結果に微妙な違いが生じます。)
シミュレーションプログラムを作る上で重要なのは、「対象を表す式」「条件」です。
対象が決まれば式は決まりますが、条件の与え方は複数あります。
どういう結果がほしいかによって、「指示したい条件」を指定するようにし、その他必要な値は計算で作り出すようにするのが、あとあと間違いの少ないプログラム作りにつながります。
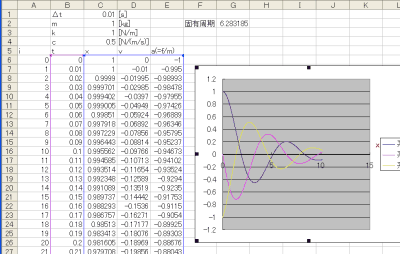 |
| バネとダンパによる振動 |
さて、結果を見比べてみます。
:
time: 1.700 x: 0.118 v:-0.674
time: 1.800 x: 0.052 v:-0.649 xが初めて
time: 1.900 x:-0.011 v:-0.619 負になるのは
time: 2.000 x:-0.072 v:-0.585 1.9秒くらい
:
time: 3.100 x:-0.440 v:-0.066
time: 3.200 x:-0.445 v:-0.019 xのマイナスの
time: 3.300 x:-0.444 v: 0.025 局地は-0.445
time: 3.400 x:-0.440 v: 0.067 あたり
:
time: 9.800 x:-0.088 v: 0.006
time: 9.900 x:-0.087 v: 0.014 10秒あたり
右のグラフと見比べると、傾向は同じようです(でなければおかしい)。
ここで、表計算の時の計算誤差で問題になった、c=0にしたときを見てみます。
本来は、xの揺れ幅は大きくなるはずはありません。が、
time: 0.000 x: 1.000 v:-0.001
time: 3.100 x:-1.001 v:-0.041
time: 6.300 x: 1.003 v:-0.018
time: 9.400 x:-1.004 v:-0.024
と、わずかずつ増えています。これでも表計算の時よりは、計算が細かくなった分だけ、ましになっています。
そこで、計算間隔をdt=0.00001秒(10マイクロ秒)にしてみます。時間が1/100細かくなったので、計算回数は100倍に増えますが、この程度ならすぐに答えが出ます。
time: 0.000 x: 1.000 v:-0.000
time: 3.100 x:-0.999 v:-0.042
time: 6.299 x: 1.000 v:-0.016
time: 9.399 x:-1.000 v:-0.026
振幅は増えなくなりました。
3.1秒のところで0.999となっているのは、3.1秒のそば(3.13あたり)で1.000になっているけど表示がとばされているだけ、3.1のときに0.999だったということです。
もう一つ、後半は時間が「9.399」のように、「9.400」のようなきりのいい数字にはなっていません。
これは、ndが10000ではなく、実は9999になっていることで起きた問題です。
本来、0.1/0.00001=10000のはずですが、0.1も0.00001もコンピュータ的にはきりのいい数字ではなく、その割り算の結果で、わずかに10000には満たず、(int)によって切り捨てられて、9999になってしまっています。
ただの(int)(iv/dt)だと切り捨てられてしまうため、(int)(iv/dt+0.5)とすると、四捨五入になって、無事10000になります。
※なぜ0.5を足して切り捨てすると四捨五入に?
やってみよう
課題
表計算の最後の課題とすっかり同一条件でやってみましょう。
振り子は、振り子の向いている角度θ(真下で0,真横で±π/2[rad])について、
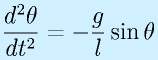
または、
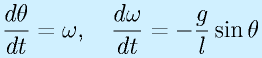
(単に角速度ωを用意して、分解しただけ)
という関係が成り立ちます。
この振り子の運動をシミュレートしてください。
なお、振り子の初期角度は「80+学籍番号下一桁[deg]」(80〜89)、振り子の長さは「3+学籍番号百の位」(4or5)でつくってください。
計算の時間間隔(dt)はお任せ、ただし、結果は「0.1秒(くらい)間隔、10秒間の計算結果」を「時刻、角度」の組で表示するようにしてください(角速度などが表示されても可、単位もお任せ)。
なお、まえのレポートの結果と比較してみるとよいでしょう。
異なる場合は、どちらかがなにか違います。
※「θ、ω」は変数名に使えないため、theta, omega などを使用。
※角度はdegからradに変換しないといけない。[rad]=[deg]/180.0*M_PI;
※例:theta=85.0/180.0*M_PI;
課題番号r05にて12/7までに提出
ヒント:
- 先ほどのプログラムをコピーして名前をpend.cなどに変え(振り子は英語でpendulum)、プログラムの「物理的な部分」を変更していきます。「シミュレーションを行う方法」の部分はそのままにしておきます。
- まず、変数を変えましょう。x,v,a,m,c,kはこの問題では使わない文字です。
たとえば、theta,omega,domega,l,g にでもしましょう。(各加速度は特に文字がないため、omegaの微分という意味でdをつけたomegaにしてみた)
- パラメータ、初期値を設定しましょう。
- 時間間隔、シミュレート時間を決めましょう。
- "a=.."に変えて"domega=?????;"を上の式をもとに書きましょう。
- "x=..", "v=.." はそのまま対応するもので、"theta=theta+???*dt; omega=omega+???*dt;" に変更。
- printfの表示を決めましょう。表示するときに[deg]で出したければ、theta等は[rad]なので変換が必要。"/M_PI*180"で[rad]→[deg]になります。
結果例:(l=3.123, g=9.80, theta0=90[deg], omega(t=0)=0, dt=0.0001)
※この通りの形式で表示する必要はなく、上記の通り、時刻と角度(この例の最初の二つの数値)が最低限あればよい。
※自分でプログラムをつったら、まずは、l,g,theta初期値をセットして、同じような値が出るかを確認するとよい。
表計算ソフトとの連携
プログラムで処理をする利点は、大量な計算、いろいろと条件で判断するような計算が容易になることですが、その一方で結果をグラフにして見やすくしたり、処理するための実験データを入力したりするには面倒です。
そこで、グラフ化やデータの扱いについては表計算に任せてみましょう。
計算結果を表計算でグラフ化
計算結果を表計算ソフトに入れることは簡単です。
まずやってみましょう。
// simucsv.c
#include <stdio.h>
#include <math.h>
int main(void)
{
int i,n,nd;
double x,v,a,m,c,k;
double dt,end,iv;
m=1.0; // シミュレーション対象パラメータ
c=0.5;
k=1.0;
x=1.0; // xの初期値
v=0.0; // vの初期値
dt=0.001; // 計算区分
end=10; // 終了時間
iv=0.1; // 表示間隔
n=(int)(end/dt); // 計算繰返数
// "(int)"は「整数にする(切捨)」という指示。
nd=(int)(iv/dt+0.5); // 表示周期
printf("time[s],x[m],v[m/s]\n"); // ★追加★
for(i=0;i<n;i++) // 繰り返し
{
a=-(k/m)*x-(c/m)*v;
x = x+v*dt;
v = v+a*dt;
if(i%nd==0) // nd回に1回表示
{
//printf("time:%6.3lf x:%6.3lf v:%6.3lf\n",i*dt,x,v);
printf("%6.3lf, %6.3lf, %6.3lf\n",i*dt,x,v);
// ★printfを修正★
}
}
return 0;
}
プログラム自体は、シミュレーションのところのバネダンパのシミュレーションのプログラムそのものです。
ただし、「★」の付いているところだけ修正してあります。
ここの「,」(カンマ)は必ず半角で入れてください。
(ので、前のプログラム simu1.c をコピーして修正した方が早い:フォルダ上でCtrl-C Ctrl-Vしてsimucsv.cに名前変更もしくはVisualStudio上で名前をつけて保存)
さて、実行すると、
$ gcc -o simucsv simucsv.c
$ simucsv
time[s],x[m],v[m/s]
0.000, 1.000, -0.001
0.100, 0.995, -0.098
0.200, 0.981, -0.190
0.300, 0.957, -0.275
0.400, 0.926, -0.354
0.500, 0.887, -0.425
0.600, 0.841, -0.489
:
9.500, -0.086, -0.021
9.600, -0.087, -0.012
9.700, -0.088, -0.003
9.800, -0.088, 0.006
9.900, -0.087, 0.014
$
と表示されます。変わったことは、最初に足したprintfの表示と、あとの修正でやたらと表示が質素になって見た目はわかりにくくなりました。
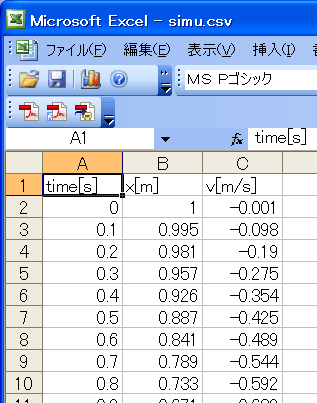 |
| CSVファイルをExcelで開いたところ |
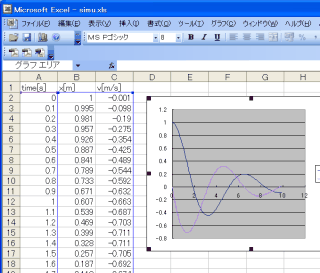 |
| グラフにしてみた |
ここで、
$ simucsv > simu.csv
$
としてください(これも全部半角、">"の右に注意。間違ってsimucsv とか simucsv.c とかすると、それらのファイルが消えてなくなります。".csv"が重要)。
さっきは画面に表示されたのが、出てこなくなります。
これは「リダイレクト」といって、printfで本来画面に出てくるはずのものを、画面ではなく、>の先、ここではsimu.csvに書き出す、という操作です。
(TeraPadやメモ帳などで開いてみると中身が見えます)。
できたファイルをフォルダで確認すると、Excelのらしいアイコンが付くので、ダブルクリックして開いてみましょう。
すると、Excelが起動し、さっき画面に表示されていた値がきれいにセルに入ります。
あとは以前と同じで、数値の範囲を選択して、グラフにしてみればOKです。
このように、
- Excelにもっていきたい数値を「,」で区切ってprintfする。
- 「実行ファイル > なんとか.csv」とすることで、結果を「.csv」ファイルにいれる。
- Excelで開く
とすれば値を持って行くことができます。
これはExcelに限らず、普通の表計算ソフトなら使える手です。
この、カンマで区切られた数値を入れた.csvなファイルを「CSV(Comma separated value)」ファイルといいます。一般的なファイル形式の一つで、数値群を扱うソフト、たとえば表計算ソフトの他、グラフ専用のソフト、計測装置なども入出力できる形式です。
で、それをプログラムから直接出させたわけです。
「>」をつかうリダイレクトは、Cygwinを含むUNIX関係のOSや、MacOSXの端末、Windowsのコマンドプロンプトなど、あちこちで使えます。使えないときは、プログラムで直接ファイルに書き出す、という操作が必要になりますが、とりあえず、この講義では避けておきます。
C言語の参考書にはふつうは載ってますので参考にしてみてください(printfのかわりにfprintfを使うようになる)。
表計算からデータをもってくる
表計算ソフト(や、CSVを出力するその他のプログラム)から、C言語のプログラムに値を持ってくることもできます。
使い道としては、CSVのデータを直接プログラムで処理したり、表計算ソフトなどでシミュレーション条件をいくつも決めた上で、C言語のプログラムに各条件でシミュレーションさせ、さらに結果を表計算に戻す、といったことも考えられます。
さて、そのためには、文字で書かれたファイルの内容を解釈しなければなりません。
しかし、このためのプログラムは、今までの数値計算とはまた別のC言語的知識(ファイルの読み込み、文字列操作)が必要となり、またプログラムも長いものとなります。
そこで、CSVファイルを読み込む部分は予め用意しました(ある意味、printfなども、標準的に用意されているもの)。それをつかって試してみましょう。
1:CSVファイルを用意する。
CSVファイルは、表計算で最小自乗法のときのデータをそのまま使います。細かい操作はこのページも参考にしてください。
- 最小二乗法実習データのページで「学生番号の下三桁を半角数字で」入力し「生成」ボタンを押す。
- 枠内に出てきた結果の「データ数,2?,」〜「2?,...」(人によってデータの数は変わります、たぶん)の範囲をマウスで選択してCtrl-C(メニュー→編集→コピー)。
以前は一行目を使いませんでしたが、今回は1行目も必要です
- Excelを開き、A1セルのところでCtrl-V(貼り付け)。 同じく、以前はA2、今回はA1
- 貼り付けたところの右下にでる小さなアイコンを左クリックし、「テキストファイルウイザードを使用」をクリック。
- 「元データの形式」で「カンマやタブ...」を選んで「次へ」
- 「区切り文字」で「カンマ」のみにチェックを入れる(最初スペースに入っているのは外す)
「データのプレビュー」で数値の間に線が入っていることを確認。
- 「完了」を押す→数値が入る。
- 「ファイル」→「名前をつけて保存」→「ファイルの種類」を「CSV()」にして、「lmsdata.csv」で保存。ファイルはcygwin/program フォルダに置くこと。
このとき2回ほど「この形式で保存していいか?」と念を押されるけど気にせずOK。
2:csv.cをとってくる。
(デスクトップの)「マイコンピュータ」→
(ネットワークドライブ)「Users(S:)」→
「Kumagai」フォルダ→
「Computer」フォルダを開いてください。
ここにある、csv.cを自分のcygwin/program フォルダにコピーしてください。
3:テストのプログラムを動かしてみる。
// csvtest.c
#include <stdio.h>
#include "csv.c" // ".c" に注意
// CSVファイルを読み込み値を得る LoadCSVとValueを含んでいるファイル
int main(void)
{
LoadCSV("lmsdata.csv");
printf("B1:%lf\n",Value(EXB,1));
printf("C2:%lf\n",Value(EXC,2));
printf("A1:%lf\n",Value(EXA,1));
return 0;
}
$ gcc -o csvtest csvtest.c
$ csvtest
ファイル 'lmsdata.csv' のサイズ:629
ファイルを読み込みました
ファイルの行数:29
B1:28.000000
C2:14.769000
セルA1は数値と認識できません
A1:0.000000
$
このcsv.cには、CSVファイルを読むためのプログラムが入れてあります。
#include することで、それを自分のプログラムに取り込むことができます。
「LoadCSV("ファイル名.csv");」 はcsvファイルを読み込みます。
エラーがあればエラーが表示され、問題なければ、「ファイルの行数:」と表示がでます。
「Value(EX?,?)」は読み込み済みのcsvファイルの特定のセルに当たる数値を取得します。
セルを表す「A1」などの「A〜Z」を「EXA〜EXZ」で、行番号を数字で指定します。
例:セル「C5」はValue(EXC,5)
なお、元のファイルに存在しないセルを指定したり、あっても数値以外が書き込まれている場合(ここまでの操作通りなら、セルA1は「データ数」という数字ではない文字)、メッセージを表示して、値はゼロになります。
4:最小自乗法のプログラムを作ってみる。
// lms.c
#include <stdio.h>
#include "csv.c" // ".c" に注意
// CSVファイルを読み込み値を得る LoadCSVとValueを含んでいるファイル
int main(void)
{
int n,i;
double x,y,sx,sy,sxx,sxy;
double D,a,b;
LoadCSV("lmsdata.csv");
sx=sy=sxx=sxy=0;
n=Value(EXB,1); // B1セルから
printf("データ数は%d\n",n);
for(i=0;i<n;i++)
{
x=Value(EXB,2+i); // i=0...n-1, データは2行から 2+i=2,3,4...
y=Value(EXC,2+i);
sx=sx + x;
sy=sy + y;
sxx=sxx + x*x;
sxy=sxy + x*y;
}
printf("SX: %lf SY: %lf SXX: %lf SXY: %lf\n",sx,sy,sxx,sxy);
// 上の行はなくても支障はない.
D=n*sxx-sx*sx;
a=(n*sxy-sx*sy)/D;
b=(sxx*sy-sx*sxy)/D;
printf("y=%lf x + %lf\n",a,b);
return 0;
}
$ gcc -o lms lms.c
$ lms
ファイル 'lmsdata.csv' のサイズ:629
ファイルを読み込みました
ファイルの行数:29
データ数は28
SX: 408.074000 SY: 3619.859000 SXX: 7818.105476 SXY: 68657.904847
y=8.499985 x + 5.401294
$
最小自乗法の説明そのものは、以前の解説を参照してください。
計算は
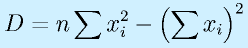
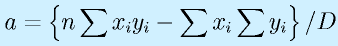
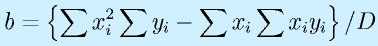
です。このプログラムでは、計算に使う
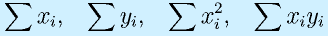
をそれぞれ、sx, sy, sxx, sxy という変数にして、最初にゼロを入れ、データの数だけforで加えています。
データの個数は1行目、B2のところにありますので、それを使っています。
以前の表計算でやったときの結果と見比べ、同じ値が得られたか確認してみましょう。
やってみよう
- 先週の振り子の課題もCSVで出力させてみる。
グラフにしたとき、以前提出したレポートと同じようなグラフがかけるかどうか?
乱数試行
乱数とはさいころを振って出る目のような、ある範囲で何が出るかわからない、という数字です。
厳密な計算をするときには不要ですが、
- ランダムな現象をシミュレーションしたいとき
- 部品などに製造上のばらつきが出ることを想定して、その影響を調べたいとき
- ゲームなどで、「運」の要素を加えたいとき
などに、コンピュータ上でも比較的つかわれます。
ここでは、「さいころ」を題材に、コンピュータの乱数を試してみます。
さいころを10回振ってみる
本当の意味の乱数は、なんの関係もなく毎回の値が出てくるものですが、C言語で使う乱数は一般に「疑似乱数」と呼ばれている、ある数式で計算される値です。
見た目はランダムに見えますが、厳密には、非常に長い周期を持った繰り返しの数列です。
ただ、たいていの場合は、乱数としてみて、あまり問題はおきません。
乱数を使うには、ただ「rand()」とします。「rand()」が使われるたび、異なる乱数が得られます。
// rand.c
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
int main(void)
{
int i,r;
srand(1225); // 「乱数の種」を固定値で指定
//srand(time(NULL)); // 「乱数の種」を現在時で指定
printf("RAND_MAX=%d\n",RAND_MAX);
for(i=0;i<10;i++)
{
r=rand() % 6 + 1;
// randは0〜RAND_MAX, % 6 することで 0〜5に
// +1することで1〜6にする。
printf("%d ",r);
}
printf("\n");
return 0;
}
$ gcc -o rand rand.c
$ rand
RAND_MAX=2147483647
2 1 3 5 6 2 6 6 3 3
※乱数なので状況で表示が変わる可能性大
$
乱数を得るための関数「rand()」は、0〜RAND_MAX までの数値の範囲でランダムに値を出します。
このRAND_MAXという値は、コンピュータやOSなどによって変わることがありますが、さしあたって非常に大きい数値です。
今回はさいころとして使うため、ほしい数値は1〜6です。そこで、
- rand()で得た値を % 6、6で割ったあまり、にする。→0〜5のいずれか。
- +1して1〜6にする
という手順で、1〜6の乱数にしています。
もちろん、rand()のうち、0と、6〜RAND_MAXが出た場合は使わない、という手もありますが、その場合は捨てる部分がほとんどで、さいころ1個分でものすごい労力が必要になります。
なお、厳密には、このさいころには偏りがでます。
0を含めてRAND_MAXまで出る種類はRAND_MAX+1=2147483648種類の数値がでることになります。
これは357913941×6+2なので、さいころにするときに4種の目が357913941回、2種が357913942回でることになります(%6+1なので、前者が3〜6、後者は1,2)。
厳密には偏りですが、実際のさいころよりは遙かに高精度なので気にする必要はありません。
(一方で、微妙な周期性が問題になることはあり)。
プログラムの先頭のほうの「srand()」は「乱数の種」と呼ばれる、初期値設定するものです。
乱数に初期値?というのも変ですが、前述の通り、周期性のあるものなので、スタート地点が設定できます。
ランダム性を重視するなら、たとえば現在時刻(time()である起点からの秒数が得られる)のような、実行時で変化するような値を種として使います。
その一方で、「ランダムだけど、再現性のある確認をしたい」という場合は、敢えて特定の適当な数字を指定します。
(srandを使わない場合は、自動的に1がつかわれたりするようです。)
上のプログラムは1225を種にしているので、何度実行しても表示される乱数の順序は変わりません。
1225を1224に変えて再コンパイルすれば、別の順番で表示されますが、それも2回目の実行で変化ありません。
コメントにしてある、srand(time()); にすれば、実行ごとにかわるでしょう。
(ただし、1秒以内に2回実行すると同じになる可能性がある)
いずれにせよ、擬似的ですが、見た目それっぽい乱数が得られます。
物事の起きる確率を実験してみる
実際に、乱数をつかって、コンピュータの中で実験をしてみます。
正しいさいころは、それぞれの目が出る確率は1/6です。
n回さいころを振ったら、n/6回、特定の目が出るはずです。
これを試してみましょう。
// rand2.c
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
int main(void)
{
int i,ok,ng,r;
srand(1225); // 「乱数の種」を固定値で指定
ok=0; ng=0;
for(i=0;i<100000;i++)
{
r=rand() % 6 + 1;
if(r==3)
{
ok++;
}
else
{
ng++;
}
}
printf("OK:%d 回 NG:%d 回 OKの率:%12.8f %%\n",
ok,ng,(100.0*ok)/(ok+ng));
return 0;
}
$ gcc -o rand2 rand2.c
$ rand2
OK:16639 回 NG:83361 回 OKの率: 16.63900000 %
※乱数なので状況で表示が変わる可能性大
$
このプログラムでは、変数 i のforループによって、何回、さいころを振るかを決めています。
その上で、さいころの目の値 r が3と等しければ「if(r==3)」、変数okに1を加えます(ok++;)。
等しくなければ、変数ngに1を加えます。
ループ終了後、結果を表示します。
ここで、okの率(r==3になった率)は、okを、ok+ng(=ループ数)で割ったものになります。
例によって、「整数/整数」だと結果が切り捨ての整数になるため、最初に%に換算するための100.0をかけてしまっています。
(特に、確率ものの場合は、普通、1未満になるので、ゼロになってしまうことが多い)。
結果は、期待通りなら、16.666...%になるはずですが、微妙に差がでます。
この差は、前述の乱数の偏りというよりは、ランダムだからこそ生じた偏りです。
srandをtime()で行ったり、別の数字に変えてみると、16.66より多くも少なくも変わります。
もう少し条件を複雑にしてみる
さいころ1個だと実験するまでもなく、予想数値がわかるので、すこし面倒にしてみます。
「さいころを2個振って、その合計が5になるのは?」
// rand3.c
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
int main(void)
{
int i,ok,ng,r1,r2; // ★変更
srand(1225); // 「乱数の種」を固定値で指定
ok=0; ng=0;
for(i=0;i<100000;i++) // ★適当に大きな数<大きすぎると終わらない
{
r1=rand() % 6 + 1 ; // r1=1〜6 ★ここ2行も変更
r2=rand() % 6 + 1 ; // r2=1〜6
if(r1+r2==5) // ★変更
{
ok++;
}
else
{
ng++;
}
}
printf("OK:%d 回 NG:%d 回 OKの率:%12.8f %%\n",
ok,ng,(100.0*ok)/(ok+ng));
return 0;
}
$ gcc -o rand3 rand3.c
$ rand3
OK:11130 回 NG:88870 回 OKの率: 11.13000000 %
※乱数なので状況で表示が変わる可能性大
$
先ほどのプログラムと変わったところは、冒頭の変数を用意するところ、さいころを振るところ、条件です。
条件を「if(r1+r2==5)」と、「2個の和が5と等しければ」に変わりました。
さて、見たところ、11%くらいですが、実際の期待値も考えてみます。
さいころを2個振ると、それぞれ1〜6がでますが、合計が5になる組み合わせは
(1,4)(2,3)(3,2)(4,1)
の4通りです。全体では6通り×6通り=36通りの組み合わせが等しく出る可能性があるため、
4/36=1/9=11.111..%
が想定される値です。
というわけで、それらしい値が得られました。
このように、「考えればわかるけど、本当に考えたことが正しいか」「考えてもわからなさそう」というときに、おおざっぱにチェックできるのが、コンピュータで乱数、の便利なところです。
なお、今回の程度のチェックでは、実際には、「全組み合わせをチェック」することもでき、その方が精度良く結果がわかります(さいころ3個で6×6×6=216通りにしかならない)。ただ、「さいころを20個ふって合計が○○になる」といった場合は、すべての組み合わせが6の20乗になるため、チェックしきれません。そういうときに非常に効果があります。
乱数の課題
rand3.cあたりを改造して、以下のようなプログラムをつくり、 レポートr06 で、プログラムとその実行結果(今まで通りのセット)を提出して下さい。
問題:
さいころを3こ振って、合計が10以下となる確率を求めてください。
ヒント:
- さいころを3個ふるようにしてください。<r1,r2に加え、r3とか
- 合計が10以下を数えてください。「10以下」はプログラムでは「<=10」と表現します。
- たぶん、半分くらい。
このページ、ここで終了。
熊谷正朗
[→連絡]
東北学院大学
工学部
機械知能工学科
RDE
[| ]
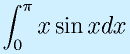
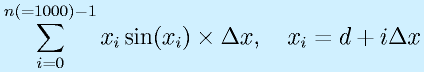
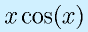 の積分を0〜πでしてみましょう。
の積分を0〜πでしてみましょう。
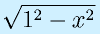 の積分を-1〜1でしてみましょう。
の積分を-1〜1でしてみましょう。

![\sum_{i=0}^{N-1}f[i]\Delta x=\Delta x\sum_{i=0}^{N-1}f[i]](eqn/prognum.bhtml.eqn5.gif)
![\sum_{i=0}^{N-1}\{f[i]+f[i+1]\}\Delta x/2=(\Delta x/2)\sum_{i=0}^{N-1}\{f[i]+f[i+1]\}](eqn/prognum.bhtml.eqn6.gif)
![]()
![f[0]+2f[1]+2f[2]+\cdots+2f[N-1]+f[N]=f[0]+2\sum_{i=1}^{N-1}f[i]+f[N]](eqn/prognum.bhtml.eqn8.gif)
![(\Delta x/2)\{f[0]+2\sum_{i=1}^{N-1}f[i]+f[N]\}=\Delta x\{\sum_{i=1}^{N-1}f[i]+(f[0]+f[N])/2\}](eqn/prognum.bhtml.eqn9.gif)
![\Delta x\{\sum_{i=1}^{N-1}f[i]+(f[0]+f[N])/2\}&=&\Delta x\{\sum_{i=0}^{N-1}f[i]-f[0]+(f[0]+f[N])/2\}\nonumber\\&=&\Delta x\{\sum_{i=0}^{N-1}f[i]+(f[N]-f[0])/2\}](eqn/prognum.bhtml.eqn10.gif)