9/13 ぷち0:力試し
Q1:
下記の行列の積をもとめよ
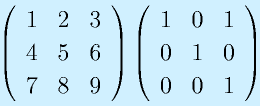
Q2:
下記の行列の固有値を求めよ
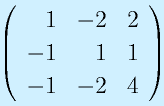
A1:
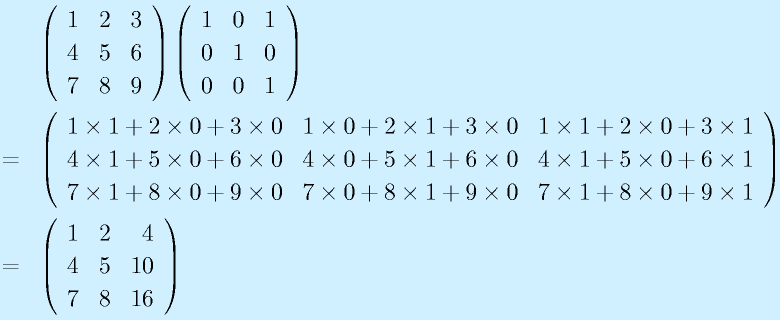
A2:
つかう数学:計算例の一番下で解説すみ。
10/12 ぷち1:固有値固有ベクトル
Q:
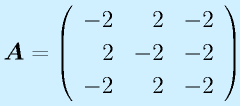
の固有値と対応する固有ベクトルを求めよ。
まず、固有値を求める。
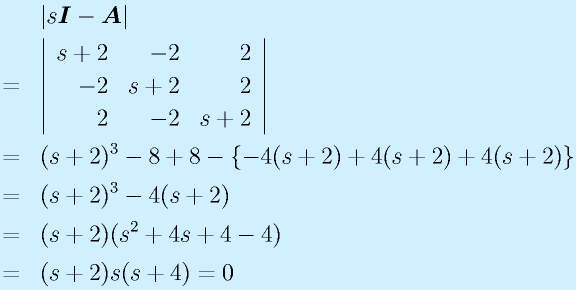
よって、固有値は0,-2,-4である。
次に、個々の固有値に対応する固有ベクトルを求める。
![]()
s1=0:
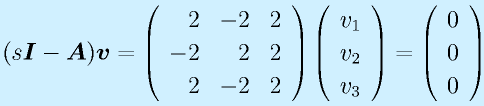
よって、
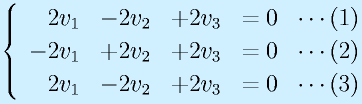
となる。(1)と(3)は同一式、また、(1)+(2)式により、v3=0が得られ、(1)にもどすとv1=v2となる。よって、たとえばv1=1とおくと、s1=0に対応する固有ベクトル、
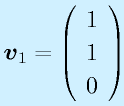
を得ることができる。
なお、
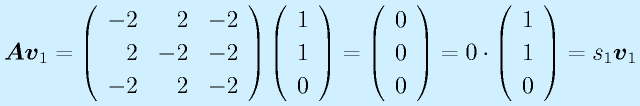
であり、固有値、固有ベクトルの関係式
![]()
を満たすことが確認される。
※v1=v2=v3=0とすると、そもそもの固有ベクトルの定義に反することに注意。
※固有ベクトルはすべての要素が0になるものが不可であって、一つの要素が0といった場合は問題ありません。。
s2=-2:
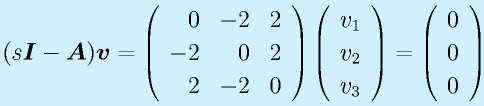
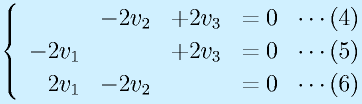
(4)よりv2=v3、(5)よりv1=v3、ついでに(6)よりv1=v2である。よってたとえばv1=1とおくと、
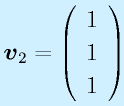
を得ることができる。Av=svの関係は各自確認すること。
s3=-4:
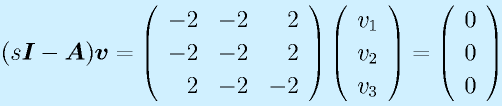
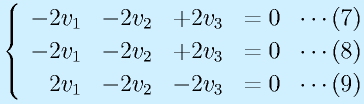
(7)式と(8)式は同一、(8)式+(9)式により、v2=0が決定する。(8)式にもどすと、v1=v3であり、v1=1とすると、
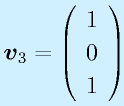
を得ることができる。Av=svの関係は各自確認すること。