アナログ回路の基礎
[| ]
最終更新: 2018/01/09 17:44:00
オペアンプで始めるアナログ回路
前ふり
一般に、電子工学系の教科書をみると、抵抗コンデンサや各種法則がおわると、次はトランジスタによる増幅の話が始まります。
トランジスタとは、電流を増幅してくれる半導体部品の基礎中の基礎ですけど、それでセンサ信号の処理回路をつくろうとすると、設計に手間はかかるし、部品もいろいろと必要になります。
(※一番やっかいなことは、センサはゼロボルトから、または負まで直流で増幅する必要があるが、トランジスタの簡単な回路は交流の増幅のみだったりする)
そこで、いきなり集積回路、ICになっている「オペアンプ(演算増幅器)」と呼ばれるものを使います。
ICというと、急にやっかいになった気がしますが、本来、ICとは「よく使う特定の機能」や「バラ部品でつくると大きくなり過ぎるもの」を1個のパッケージに小さく収めたもので、「使いやすく」なっています。もちろん、その分、1個1個は複雑になっていますが、同じものを自分で組み上げるのに比べたら、という意味です。
ここで使うオペアンプはその点、動作は簡単で使いやすく、バラ部品で同じ機能を果たすのに比べたら劇的に回路が簡単になります。知っておいて損はありません。
オペアンプとは
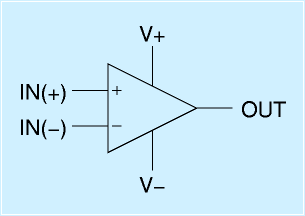 オペアンプは「オペアンプ」(Operational Amplifier)と呼ばれる、増幅機能をもった回路です。そのため、必ずしもICの形をしているとは限りませんが、オペアンプというICも多く市販されていて、普段はそれをつかいます。
オペアンプは「オペアンプ」(Operational Amplifier)と呼ばれる、増幅機能をもった回路です。そのため、必ずしもICの形をしているとは限りませんが、オペアンプというICも多く市販されていて、普段はそれをつかいます。
オペアンプは一般に電源端子を2本、入力端子を2本、出力端子を1本持っています(さらに調整用などの端子を持つことあり)。そこで、一般に右に示すような右向きの三角形に線を生やした図を、回路図では使います。
- 端子 V+ V-:オペアンプを動作させるための電源をつなぎます。電源が無ければ動きません。なお、時と場合によっては、V+,V-ではなく、VCC, VEE と表記されること、+15 -15 と具体的に書かれることなどがあります。
- 端子 IN(+) IN(-):信号の入力端子です。正と負の入力があります。それぞれの端子の電圧を Vin+/Vin-、VP/VN と表記することがあります。
- 端子 OUT:信号の出力端子です。その端子の電圧を Vout Vo と表記することがあります。
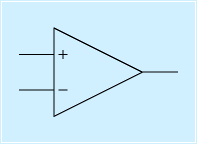
さて、オペアンプ、電源が無ければならないのは当たり前なので、回路図を書くときはしばしば省略されます(回路図の隅の方に、別途電源供給の指示を書くなど)。また、記号の形状から、OUTもわざわざ表記する必要はありません。さらに、入力も、記号の中に+−が書いてあるので、それで十分です。
そのため、一般には右図のような形で書かれます。この講義でも特に明示する必要がない限りこう書きます。
なお、この+と−の印はとても重要です。回路を書きやすくするため、オペアンプの記号も左右に向きを変えたり、上下を反転させることがあり、+−がないと、入力が逆になってしまうためです。
蛇足:めったに上向けたり下向けたりはしません。また普通は右向きに統一します。
なお、実際のオペアンプのICでよくあるタイプは、
- 足が8本で2個のオペアンプが入っていて(2*3)、2本が電源(共通)
- 足が14本で4個のオペアンプが入っていて(4*3)、2本が電源(共通)
- 足が8本で1個のオペアンプが入っていて、2本が電源、そのほか微調整端子など
というパターンです。使う数によって選定します。
蛇足:1個に多くはいっているほうがいくつか利点があります。が、どうしても回りに抵抗とかコンデンサをつけるため、窮屈になることがあります。
オペアンプの特性
オペアンプの特性を一言で言うと、
「入力端子の電圧差(電位差)を非常に増幅して出力する」
です。式で書くと、
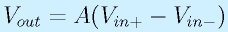
となります。Aは電圧増幅度といい、一般的なオペアンプで、1000倍(10^3)〜100万倍(10^6)と大幅な増幅をします。
この極端に大きな増幅能力を、敢えて限定して使うことで、その余力で増幅の安定性を高めるような使い方をします。
実在のオペアンプはいろいろな制限があります。
- 増幅率が大きいとはいえ、限りはある。
- 中身も回路なので、入力端子には電流が流れる。
- 出力できる電流には限度がある。
- 出力できる電圧に限度がある。たとえば、電源として、+15[V]、-15[V]を与えると、出力は一般的には -13〜+13[V]程度の範囲に限定される(2[V]削れる)。特殊なものでも、+15, -15 を越えることはできない。
ですが、回路を解析するとき、いちいち気にしていられないので、以下のような仮定を置きます。
- 増幅率は∞。
- 入力端子に電流が流れない。
- 出力電流はいくらでも流せる(吐出し/吸い込みとも)。
- 電圧の限度も考えない。
これを理想オペアンプといいます。理想と現実のギャップは一般論として問題になることが多いのですが、オペアンプはこの理想オペアンプに近づけるように設計されているので、前2項目については、普段はほとんど気になりません。後者は、回路にあったオペアンプを選定することになります。
このようなオペアンプを使うと簡単に?各種回路が作れます。以下ではそれらについて見ていきます。
増幅回路1
ここでは電気信号の処理の基本中の基本、増幅回路を見てみます。
反転増幅回路
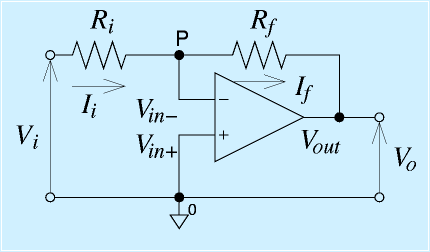 オペアンプを使った増幅回路で一番基本となる、反転増幅回路を見てみます。
オペアンプを使った増幅回路で一番基本となる、反転増幅回路を見てみます。
反転増幅回路は文字通り反転しつつ増幅、つまり、単に大きな電圧になるのではなく、正負の極性が反転します。次に非反転増幅をやりますが、まずは簡単な反転増幅から。
右の図のような回路を考えます。入力電圧Viを増幅して、Voを出力します。
ここで、オペアンプは入力端子にほとんど電流が流れないため、入力端子からP点に抵抗Riを通して流れてくる電流Iiと、オペアンプの−端子と出力端子をつないでいる抵抗Rfを流れる電流Ifは等しくなります。
このことを念頭に、式を立てます。なお、図中に記したV??は、各点の基準電位(▽0)からの電圧です。
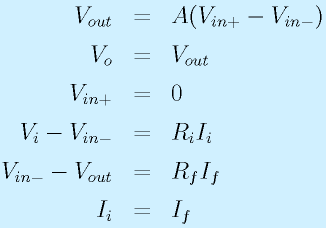
ここで、Aは電圧増幅度です。
まず、最初の3式より、
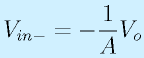
また、後半3式より
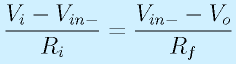
となります。これを整理すると、
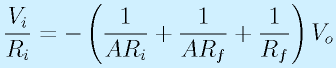
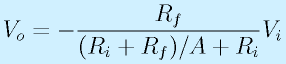
ここで、オペアンプの増幅度Aは無限大とみなせるので、
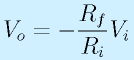
となります。
つまり、この回路では、2本の抵抗の比で、電圧の増幅率(利得、ゲイン)を決定できます。
さてここで、オペアンプを使った回路の重要な特徴を見ておきます。
特徴1:
この回路は常に出力の安定を保つような動作をしています。なにかの拍子に(たとえば、オペアンプの電源の変動や後ろにつなぐ回路の特性)で出力電圧がわずかに上がったとします。そうすると、それに釣られてP点の電圧も上がります(これもまた内分回路の1つ)。そうすると、オペアンプの−入力端子の電圧が上がるため、オペアンプの出力は下がり、打ち消されます。逆に、わずかに下がったとすると、上げる方向に動作します。
これは出力が−端子に抵抗を介してつながっていることによる動作で、負帰還(ネガティブフィードバック)と呼ばれています。制御工学でもでてくる概念です。
オペアンプは負帰還をかけているときはこのような動作になります。
特徴2:
オペアンプで負帰還がかかっていて、正常動作している場合は、つねに−入力が+入力に一致するように出力電圧が決まります。ずれていると、それが大きく増幅されて出力され、帰還抵抗を通じて−入力に届くためです。この状態は一見すると+端子と−端子が電流は流れないもののつながっている(ショートしている)ように見えます。そこで、これを バーチャルショート (仮想短絡)と呼びます(本によってはイマージナリショートと記載)。今回の回路のように、Vin+端子がGND(0V)に接続されている場合は特に仮想接地と呼びます。この仮想接地は、演算や変換をするときの基本になります。
非反転増幅回路
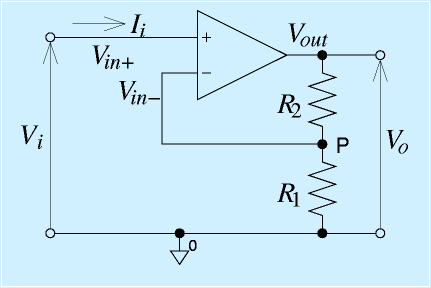 次に、非反転増幅回路を見てみます。
次に、非反転増幅回路を見てみます。
非反転増幅回路は右の図のような回路を使います。
P点の電圧(=Vin-)は、VoutをR1とR2で分圧したものであることに着目。
まず、
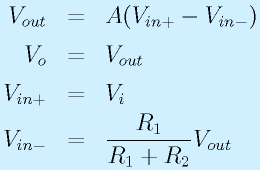
の各式が成立します。適宜連立させると、
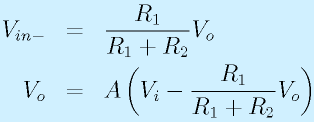
なので、
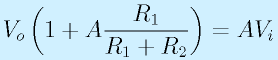
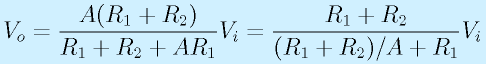
ここで、Aを∞とすると、
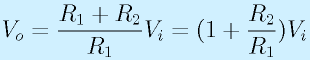
となります。つまり、(1+R2/R1)の倍率で入力電圧が増幅されてでてきます。
もしくは、さっきの仮想短絡の考え方を適用すると、単に、
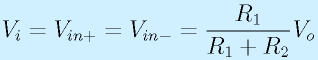
から直接求まります。
この非反転増幅回路はとても便利な特徴があります。それは回路の入力がオペアンプの入力そのもの、つまり、直前の回路から電流が流れてこないという点です(入力インピーダンスが高い)。これは前の回路に負担をかけないという利点があります。センサのわりと多くは電流を引き出すような使い方をすると出力電圧に影響が出ます。そういうとき、この非反転増幅をつかいます。
先ほどの反転増幅は、入力と、仮想接地した点の間に抵抗Riが入っているので、Iiの電流が流れてしまいます(入力インピーダンスRiという)。
唯一の難点は、1倍未満がつくれないことです。増幅なのに1倍未満が必要かというと、電流が流せない回路と電流を要求する回路の間にはさんで「電流を増強」する場合には、たまにそういうことがあります。そのときは、前の回路にもよりますが、分圧した上で増幅ということもやります。
抵抗の選定
これらの回路はあくまで「抵抗比」で増幅率が決まります。
では、どんな抵抗を使っても良いのでしょうか?
たとえば、10倍の非反転増幅を行うときに、1[Ω]と10[Ω]をつかったとします。
入力に1[V]かけると出力は-10[V]ですが、このとき、各抵抗には、Ii,Ifとして1[A]流れることになります。直前の回路に悪いばかりか、そもそも、10[V]で1[A]流せるオペアンプは特殊な部類(パワーオペアンプ)が必要になります。
これら回路では、基本的に電流は流す必要がほとんど無いため、より大きな抵抗を選定すべきです。ただ、実在のオペアンプでは、入力端子に多少は電流が流れてしまうため、極端に大きな抵抗も選べません。
おおざっぱな目安としては、バイポーラ型オペアンプ(という種類があります)でRf=10[kΩ]程度、FET型オペアンプでRf=100[kΩ]程度がよいでしょう(後者のほうが電流が流れにくい)。
次に抵抗値の選定です。抵抗は、好きな値の抵抗が入手できるわけではありません。一般に入手しやすいのは以下の値です。
10,11,12,13, 15,16,18,20, 22,24,27,30, 33,36,39,43, 47,51,56,62, 68,75,82,91
×0.1, 1, 10, 100, 1000, 10000, 100000
(1[Ω]〜10[MΩ])
この数字の並びをE24系列といいます。半端な数字が並んでいるように見えますが、数字が1つ進む毎に概ね1割増しです。
つまり、増幅率を決めるときはこれらから作れる比となります。
ただし、一般には制約にはなりません。だいたいは「10倍くらい」といって回路を設計するので、細かい値を気にしてもしょうがないです。細かい調整は、センサそのもの特性の補正と込みで、コンピュータ上でやります。
どうしても、という場合は、抵抗の直並列つなぎ、可変抵抗(半固定抵抗)などを使います。その場合は抵抗の精度も気にする必要があります。
なお、そこそこまじめに増幅回路などを作るときは、金属被膜抵抗(通称1%抵抗)を使います。これは温度による変化も少なく、安定した増幅回路を作ることができます。
どうでしょう? 回路を設計するというと難儀しそうですけど、電圧を数倍する回路だけで言えば、抵抗2本で決めるだけです。これから出てくる回路の多くは、これらの応用です。
演算回路1
加算回路
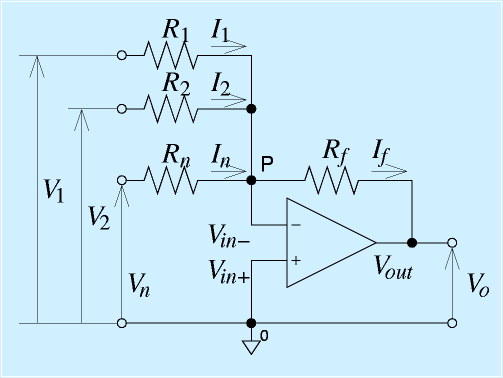 複数のセンサの出力を合成したり、ある信号に、電圧のゲタを履かせたり(=単純に1V加えるなど)するときに必要になるのが、加算回路です。
複数のセンサの出力を合成したり、ある信号に、電圧のゲタを履かせたり(=単純に1V加えるなど)するときに必要になるのが、加算回路です。
加算回路は右のような形をもっています。簡単に気づくとおもいますが、これは反転増幅回路の入力が単に増えたものです。これがどういう風に動作するか考えてみましょう。
今回は最初から仮想接地を使います。仮想接地のため、P点は0Vと考えます。
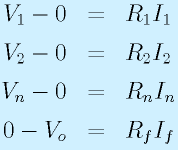
また、キルヒホッフ第一の法則より、

これらをまとめると、
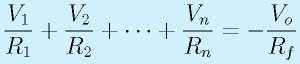
よって、
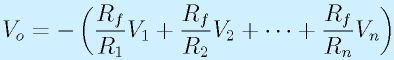
となります。すべて同じ値の抵抗を使うと、
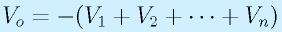
です。
この回路は複数の入力電圧を適当に抵抗比で重みをつけながら加算することも可能です。
なお、非反転で同じようなつなぎ方をすることはできません。
加減算回路
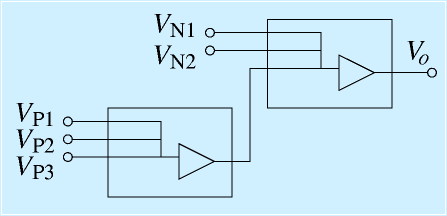 先ほどの加算回路は加算といいつつ、反転も入っています。
そこで、右の図のように2個つなぐと加算と減算をまとめていろいろ入力できます。
VPの側の入力からは2回反転するので、正負そのまま、VN側は反転します。あとは抵抗値を適宜選ぶことになります。
先ほどの加算回路は加算といいつつ、反転も入っています。
そこで、右の図のように2個つなぐと加算と減算をまとめていろいろ入力できます。
VPの側の入力からは2回反転するので、正負そのまま、VN側は反転します。あとは抵抗値を適宜選ぶことになります。
なお、単なる減算については、あとで「差動増幅回路」という差を取る回路がでてきますので、それを使います。
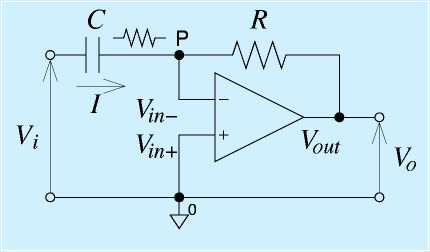
積分回路
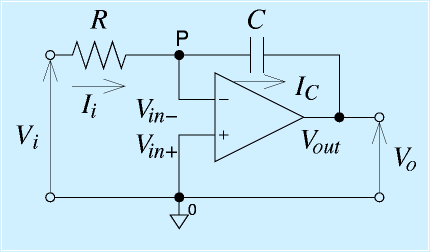 反転増幅回路の抵抗を一本、コンデンサに変えると積分回路がつくれます。
反転増幅回路の抵抗を一本、コンデンサに変えると積分回路がつくれます。
右図の回路では、
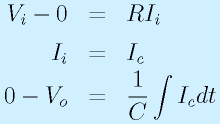
が成立します。反転増幅と違うところは、電流を積分すると電荷、電荷をCで割るとコンデンサの端子電圧です。
これを解くと、
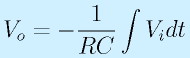
となり、入力電圧を積分する回路になります。
実用上は、コンデンサに並列に大きな抵抗を入れることがあります。本来積分はどんどんたまってしまうものですが、抵抗が並列に入っていると、適当に電荷が抜けて飽和しなくなります(もちろん、積分からずれます)。または、コンデンサに並列に電子スイッチを取り付けて、コンデンサを空にする仕掛けをつけます。
微分回路
 コンデンサと抵抗の位置を逆にすると微分回路を作ることができます。
コンデンサと抵抗の位置を逆にすると微分回路を作ることができます。
右図において、
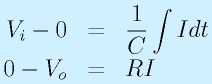
なので、
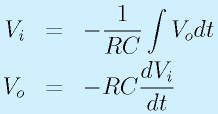
となります。
ただし、実用上、これをそのままつかうとひどいことになります。微分というのはその性質上、ノイズのような激しく変化するものを拡大します。そのため、コンデンサと直列に適当な抵抗を入れて、微分として動作する周波数を低く抑えます。
以上のように、それほど難しいことなく、加減算や微分積分回路がつくれます。
オペアンプが「演算増幅器」とよばれるのは、このように演算回路に使いやすいという意味もあると言えます。こういった回路を大規模に組み合わせてつくったものを「アナログコンピュータ」といいます。微分方程式などを実際に解くことができます。
増幅回路2
ここで先の基本的な増幅回路の延長で、やはり良く使われる増幅回路を中心に示します。
ボルテージフォロワ
 増幅回路の主な役目の一つは電圧を大きくするという意味の増幅です。
もう一つの意味が、「電圧は変えないけど、大きな電流出力に耐えられるようにする」増幅です。
専門的には「(出力)インピーダンスを下げる」とも言います。
多くのセンサや受動部品(抵抗、コンデンサ)を組み合わせた回路は、それに続く回路で電流を吸ってしまうと特性に影響を受けます。そのため、なるべく電流を流すこと無く、電圧だけを後ろに伝えることが重要です。ですが一般的な用途では電流を吸ってしまう回路が多いため、その間で電流だけ増やす必要があります。
増幅回路の主な役目の一つは電圧を大きくするという意味の増幅です。
もう一つの意味が、「電圧は変えないけど、大きな電流出力に耐えられるようにする」増幅です。
専門的には「(出力)インピーダンスを下げる」とも言います。
多くのセンサや受動部品(抵抗、コンデンサ)を組み合わせた回路は、それに続く回路で電流を吸ってしまうと特性に影響を受けます。そのため、なるべく電流を流すこと無く、電圧だけを後ろに伝えることが重要です。ですが一般的な用途では電流を吸ってしまう回路が多いため、その間で電流だけ増やす必要があります。
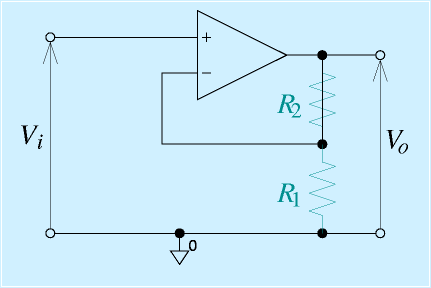
この目的で使われるのがボルテージフォロワです。
回路はとても簡単で、右図に示すようにオペアンプの出力と−入力を接続しただけです。
これは、見方によっては、非反転増幅回路の一種です。非反転増幅では、出力電圧は
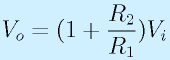
で得られました。ここで、ボルテージフォロワの接続では、R2=0(直結)、R1=∞(無接続)に相当します。すると
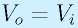
が成り立ちます。
なお、本によっては「ボルテージホロワ」と書いてあります(長いこと「ほろわ」ってなんだろ、と疑問に思っていましたが、ある日「follower」(follow+er)だと気づいて納得しました。)。
また、オペアンプにとって、この接続はつらい(発振しやすい)使い方で、特殊なオペアンプではこの接続での動作を保証していないことがあります(普通は大丈夫)。
差動増幅回路
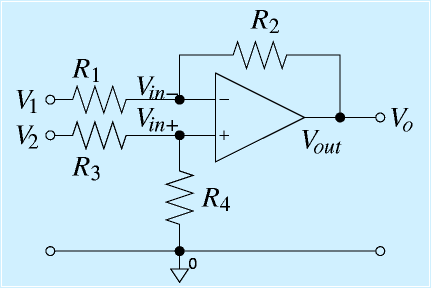 差動増幅回路は2つの電圧の差をとって増幅する回路です。演算と言うよりは増幅に分類されています。
差動増幅回路は2つの電圧の差をとって増幅する回路です。演算と言うよりは増幅に分類されています。
差動増幅回路は右の図に示すように、オペアンプに抵抗を4本接続して作ります。
以下、動作を見ていきましょう。
まず、─入力端子の電圧を求めます。これは反転増幅回路と同じように考えて、
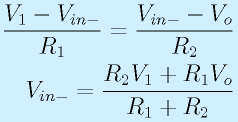
となります。+入力端子は、単純にV2を分圧したものなので、
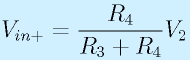
です。仮想短絡が成り立っており、
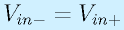
なので、
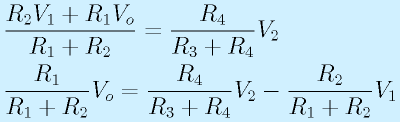
となります。
ここで、簡単のため、R1=R3, R2=R4とおくと(実際の回路でも普通はそうします)
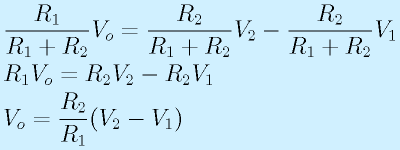
となり、 [V1とV2の差をとって増幅する回路] になります。
 この差動増幅回路は文字通り差をとることに使えますが、実際のセンサ用途では発展型である次のインスツルメンテーションアンプが使用されます。
この差動増幅回路は文字通り差をとることに使えますが、実際のセンサ用途では発展型である次のインスツルメンテーションアンプが使用されます。
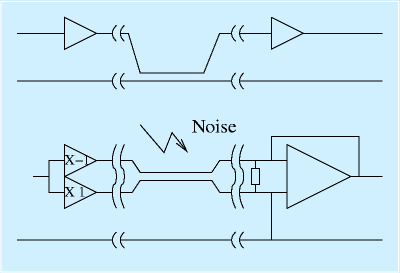
ですが、差動増幅には、もう一つ、信号の送受信という主な使い道があります。
右図に概略を示します。
普通、電気信号を伝えるためには、基準となる線(GND)と、具体的に伝える信号をセットにします(右図上)。安いマイクの端子や、テレビとビデオをつないだり、ゲーム機とテレビをつなぐ赤白黄の同心円のプラグは良く見ると電極が2個あり、外側(根本)の面積の大きい方が一般にはGND、中心(先端)の電極が信号です。
ところが、異なる電化製品をつないだ場合に、様々な原因により、電圧信号が正しく伝わらず、不要な信号(ノイズ)が信号線に入り込むことがよくあります(電圧が比例して落ちるだけ、は平和な部類)。外から入ることもありますし、本来は固定のはずのGNDが乱れることもありますし、複数の信号を同時に送る場合はそれらが相互に混入(クロストーク)することがあります。
音なら聞こえる雑音になりますし、映像だと多少乱れたりします。これは、距離が長くなればなるほど、ひどくなります。
そこで、信号の線を2本にする方法が使われる場合があります(右図下)。2本の信号線の一方は、送るべき電圧をそのままに、もう一方の線は「×−1」して送ります。これを差動増幅回路で受取り、もとの信号に戻します(この図の場合、信号は最終的に2倍になっています)。
これは、そういう雑音は、「近接する、同じ性質の線には、同じように入る」という傾向が強く、雑音をnとすると、Vおよび-Vを送信した場合に受け側ではV+n, -V+nを受信、この差をとると2Vとなって、雑音がキャンセルされます。
そのため、高級なオーディオ、体育館で使うような(=線がものすごく長い=ノイズが入りやすい)マイクなどでは、この基準+信号2本で送る方式、差動伝送、平衡伝送がつかわれています。形は多少異なりますが、ネットワークのケーブルなども、この方式です。
なお、一見すると、この方法、GNDがいらなさそうですが、受け側のオペアンプはあくまで自分の電源電圧の幅しか受け入れられません。そのため、両者の基準は「ほぼ」合わせておく必要があります。
インスツルメンテーションアンプ
 上述の差動増幅回路は大きく二つの問題点があります。
上述の差動増幅回路は大きく二つの問題点があります。
- 入力抵抗が(オペアンプ本来やセンサ類に対して)低い=電流が流れる
- 入力抵抗がアンバランス(両入力が非対称)
そのため、センサなどに使うには問題が出ることがあります。
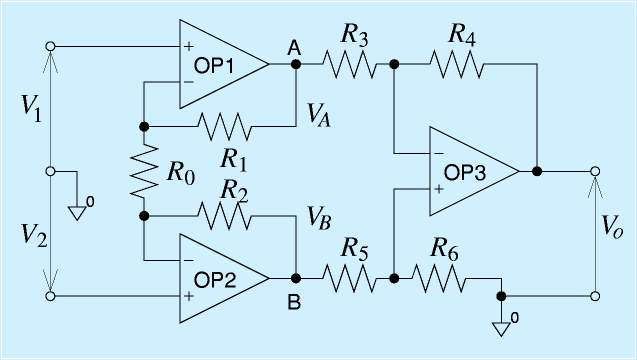
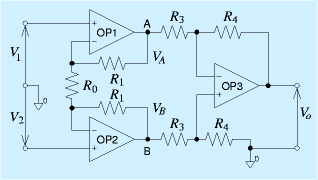
それを改良した物に、インスツルメンテーションアンプ(Instrumentation:計測 amp)があります。
これは右図のような回路をしています。オペアンプが3個もありますが、部分毎に見てみます。
まず、OP3についてみると、A,B端子間の差動増幅になっています。これらの端子はオペアンプOP1,2の出力端子に直結なので、上で述べたような、入力端子の問題の影響は基本的にありません(電流が流れても電圧が変わらないことになっている)。そのため、出力電圧Voは、R3=R5、R4=R6の条件の下で、
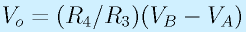
となります。
さて、本体のOP1, OP2について考えます。この回路でも仮想短絡を前提とすることができます。
そのため、両オペアンプの+入力端子と−入力端子は同電圧と見なせます。
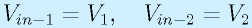
ここで、点Aと点Bの間の経路を考えます。点Aから抵抗R1,R0,R2を通る点Bまでの経路は、OP1, OP2の入力端子には電流が流れないことから、各抵抗に同一電流が流れます。そのため、
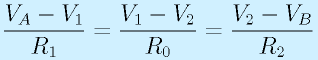
が成り立ちます。よって、
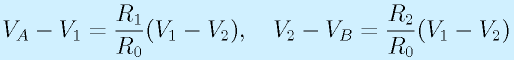
この2式の辺々を加えると、
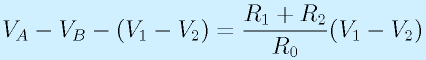
よって、
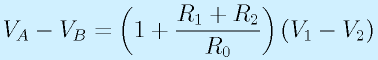
となります。
 以上、まとめると、
以上、まとめると、
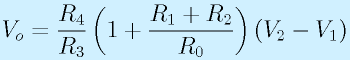
となります。なお、一般には、R1=R2と選びます。これまでの抵抗の統一と合わせると右図のようになります。
この回路の特徴は
- 両入力とも、オペアンプ直結の高入力抵抗なので、微弱な出力のセンサ類に向く。
- 一回路で増幅率を稼ぎやすい。
- 抵抗R0を可変すれば増幅率を大きな範囲で可変できる。
などです。同じインスツルメンテーションアンプには、オペアンプ2個、抵抗4本のみで構成する回路もあり、そちらのほうが低コストにはなりますが、上記の2,3番目の利点は持ちません。
センサが、「差を取る」必要があり、かつ電流が流せない場合には、何も考えずにこの回路を採用してみるといいでしょう。
なお、理想オペアンプでは、非反転増幅回路2個をただの差動増幅につないでも似た結果が得られますが、実在回路の場合は、電圧の飽和(出力が電源いっぱいになってそれ以上でなくなる)のしやすさで大きな違いがあります。
電流−電圧変換回路
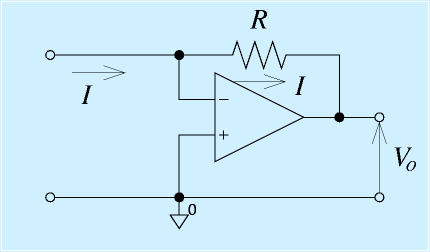 センサの中には、その出力が電流のものがあります。たとえば光系のセンサは、光量に比例した電流が出力されます。これを電圧に変換し、必要に応じて増幅するものに、電流電圧変換回路があります。
センサの中には、その出力が電流のものがあります。たとえば光系のセンサは、光量に比例した電流が出力されます。これを電圧に変換し、必要に応じて増幅するものに、電流電圧変換回路があります。
回路図を右図に示します。反転増幅回路から抵抗を一本とった形になっています。
このとき、入力端子から電流Iが流れ込むと、仮想接地によって、Vin-端子は0V、なので、
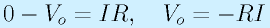
という簡単な式になります。電流値を抵抗値で倍数した物が出力にでてきます。
なお、直前の電流を出力する回路は、「GND(0V)に向って電流を流す」仕様になっている必要があります。
次に扱う電流出力アンプは対応していません。
電流出力アンプ(定電流回路)
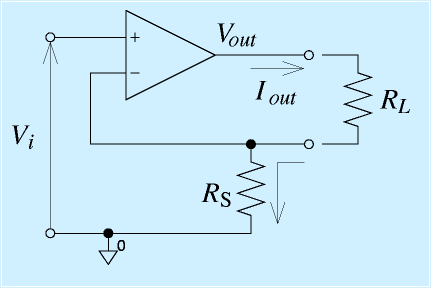 相手が電子回路の時には、電流出力で信号を渡すことはあまり多くありません。まれに信号の送受で使われることがあります(電圧は途中の抵抗で減りますが、電流は分岐しなければ減らないため)。電子回路の中では電流源はときどき使われますが(オペアンプ自身の中にもいくつかあります)、普通は一定の電流です。
相手が電子回路の時には、電流出力で信号を渡すことはあまり多くありません。まれに信号の送受で使われることがあります(電圧は途中の抵抗で減りますが、電流は分岐しなければ減らないため)。電子回路の中では電流源はときどき使われますが(オペアンプ自身の中にもいくつかあります)、普通は一定の電流です。
ところが、機械との兼ね合いを考えると、電気→力の変換をする代表的なものである、コイル、電磁石、およびその派生であるモータなどは、電流と力が比例するため、電流を調整する必要があります(簡易的には電圧調整でも問題ありませんが)。
そこで必要になるのが、電流出力アンプ(定電流回路)です。
定電流回路を右図に示します。形は非反転増幅回路に似ていますが、考え方が違うので、別物として考えます。
これまでの回路は出力がなにもつながっていなくても動作しますが、これに関しては出力がつながっていなければ動作しません。そこで、出力に負荷抵抗RLがつながっていると考えます。
負荷抵抗の性質などにも影響を受けますが、仮想短絡が働いていると考え、−入力端子は、Viと同じ電圧とします。
ここで、抵抗RLの大きさなどは考えずに、オペアンプのVoutからRLを通して、電流Ioutが流れるとします。
流れた電流は、この回路に戻ってきますが、オペアンプの入力には流れないため、全部、抵抗RSに流れます。
この、RSの両端に生じた電圧RSIoutが、オペアンプの─入力端子の電圧となります。よって、
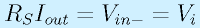
が成り立ち、
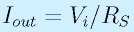
となります。つまり、入力電圧に比例した電流を負荷に流すことができる回路になります。
なお、出力電圧は、「この電流が流れるように」自動的に決まります(RsIout+RLIout+その他要因)。たとえば、モータは回転数が上がると逆起電力という電圧が生じるため、一定の電圧をかけていると徐々に電流が減ります。この回路を使うと、その分も込みで出力電圧が調整され、電流が指定通りになるように機能します。
この回路の注意点は、
- 仮想短絡が成立するように場合によっては回りにいろいろ工夫がいる。
- 出力電圧は負荷抵抗RLによって変る。とくに、出力を解放する(抵抗無限大)と最大出力になるので、回路を切る/接続する可能性がある場合は要注意。
- 負荷は電源にもGNDにも直接接続できないこと(フローティング=浮いている)という。
電磁石、モータなどは一般に問題は少ない。
- 普通のオペアンプでモータなどを動かすことは出力が足り無すぎて不可能。
大出力のパワーオペアンプを使うか、オペアンプのパワーアップ回路(出力ブースト回路)を追加する。
などがあります。電源やGNDに直結したい場合には、別の工夫をする必要があります(電源につなぐのは案外簡単、GNDに繋ぐのは全く別の回路が必要)。
演算回路2
これまでは、入力と出力にある種の比例関係がある、素直な特性の回路を扱ってきましたが、この節では現実にはなくてはならない、いろいろと小細工?するための回路を示します。
検波・絶対値回路
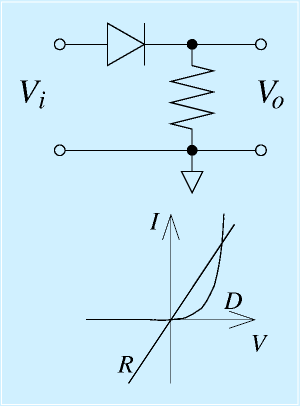 信号を処理する場合に、信号の正の部分だけほしい、もしくは、絶対値がほしい、という場合があります。
信号を処理する場合に、信号の正の部分だけほしい、もしくは、絶対値がほしい、という場合があります。
たとえば、マイクなどから入ってきている信号の大きさを検出したい場合、単に平均値をとるとゼロになってしまいますが、正の部分だけをとって、もしくは絶対値をとってから平均化すると、信号の大きさに比例した信号がえられます。
(AMラジオもある特定の周波数の電波の強弱で音が伝えられてくるため、このような処理をします。)
この目的で、一番簡易的に用いられるのは、右に示すような回路です。
ここで、三角に棒が一本ついたような記号が初登場しましたが、これはダイオードという半導体部品の一種です。
ダイオードは、三角の向いている方向には電流を流し、逆向きにはほとんど流さないという特性を持ちます。
これをグラフにしたのが、右図の下です。横軸に電圧、縦軸に電流をとり、加える電圧と流れる電流の関係をグラフにします。
抵抗の場合は、E=RIなので、電圧と電流は比例するので直線になります。
ダイオードの場合は、電圧が流れない方向にかかっている場合(電圧負)、電流はほぼゼロです。
流れる方向に電圧がかかると、ある程度電圧があがったところで急に電流が流れ始めるようになります。
理想的には正になったらすぐに流れてほしいのですが、実際にはこのような特性になり、この流れ始めるあたりの電圧を「順方向降下電圧」と呼びます。一般的に入手できるシリコンダイオードで0.6〜0.7[V]程度、低めのもので0.4[V]程度などですが、ダイオードの種類や流す電流によってこの降下電圧は変ります。
さて、正の部分だけをおおざっぱに得るにはこの回路で十分ですが、この順方向降下電圧分目減りすることや、電流によって特性がかわることなどもあり、正確な計測にはつかえません。そこで、オペアンプを併用した回路をつかいます。
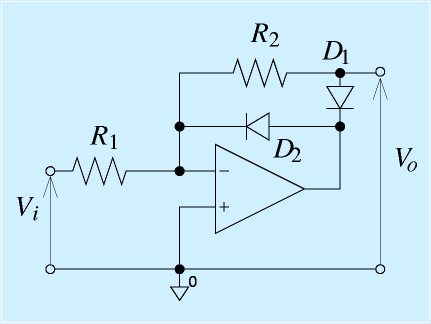 右図にその回路を示します。反転増幅回路にダイオードが2本追加されています。
右図にその回路を示します。反転増幅回路にダイオードが2本追加されています。
まず、単純な反転増幅回路の場合は、入力Vi>0の場合は出力Vo<0となり、Vi<0の場合はVo>0となります。
この回路において、Vi>0が入力された場合、R1を通って流れ込んだ電流は、D2は逆向きなので、R2に流れます。出力になにもついていない(もしくは、ほとんど流れていかない)場合は、その電流は、D1を通ってオペアンプの出力端子が吸い込みます。
これによって、反転増幅回路と同じような動作となり、Vo=-(R2/R1)Viとなります。
逆に、Vi<0が入力された場合、オペアンプ−入力端子から、R1を通って入力側に電流が流れていきます。その電流は、正方向なのでD2を通って、オペアンプから流れてくることができるため、仮想接地が成り立ちます。この状態で、オペアンプの出力はD2の順方向降下電圧だけあり、Voに外部からむりに正の電圧が加えられない限りはD1は逆電圧がかかった状態になるため電流が流れません。その結果、仮想接地の0[V]にR2を通じて出力をつないだようになります。
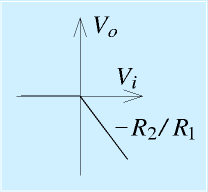 以上まとめると、
以上まとめると、
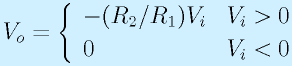
となります。この回路を直線検波回路と言います。
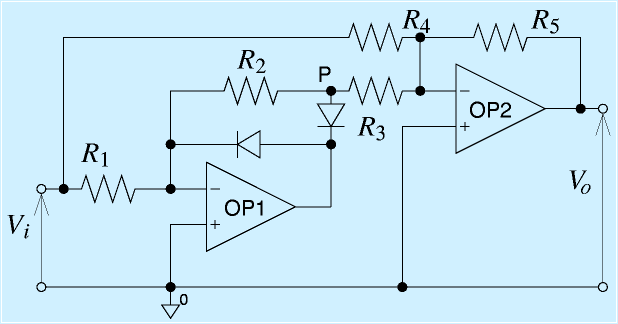 これを応用すると、絶対値回路を作ることができます。
右のような回路を構成し、R1=R2=R3=R, R4=R5=2Rとします。
これを応用すると、絶対値回路を作ることができます。
右のような回路を構成し、R1=R2=R3=R, R4=R5=2Rとします。
まず、入力ViからOP1を経てP点に至る回路は先ほどの直線検波回路です。R2=R1なので、
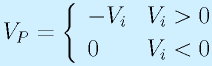
です。つぎに、ViおよびP点からOP2を通して出力Voに至る回路は、以前やった加算回路です。
この回路は、, R4=R5=2R3と仮定しているので、
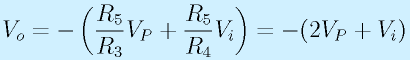
となります。
以上、組み合わせると、
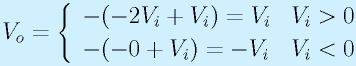
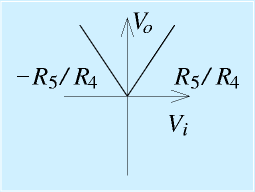
となります。これは

に他ならない、絶対値を求める回路になります。
 ここでは、R5=R4=2R3と置きましたが、R4=2R3のまま、R5を変えると、
ここでは、R5=R4=2R3と置きましたが、R4=2R3のまま、R5を変えると、
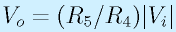
となります(加算回路部分より明らかです)。
フィルタ回路
実際にいろいろな信号を扱っていると、不要な信号を取り除きたくなることがあります。
不要な信号といっても千差万別で対処法も様々ですが、周波数で要不要がわけられるとき、フィルタと呼ばれる回路を使用することができます。
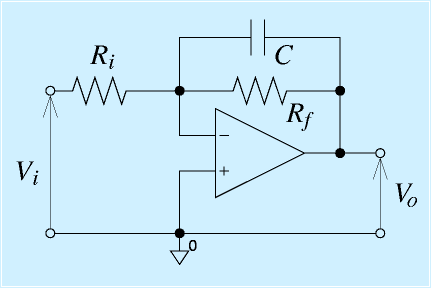 右図はローパスフィルタと呼ばれる、周波数が低い成分だけを通し、周波数が高くなるほど信号が小さくなるような回路です(もっとも初歩的な構成)。
右図はローパスフィルタと呼ばれる、周波数が低い成分だけを通し、周波数が高くなるほど信号が小さくなるような回路です(もっとも初歩的な構成)。
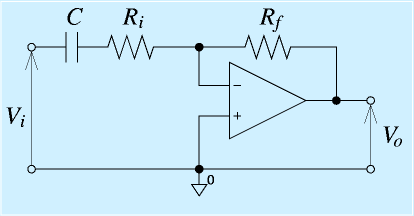
反転増幅回路のオペアンプの出力と入力−をつなぐ抵抗Rfに、コンデンサCを並列に接続しています。
コンデンサが無い場合の電圧増幅率は(Rf/Ri)です(符号略)。
さて、コンデンサは、その電流の流れやすさが周波数によって変わるという説明を以前しました(→参照)。その、抵抗に相当するような値(インピーダンス)は(1/2πfC)で表されることを示しました。
抵抗RfとコンデンサCの並列つなぎを考えると、周波数が十分低い場合、(1/2πfC)がRfに比べて大きくなるため、並列つなぎしたものの抵抗はほぼRfになります。そのため、周波数が低い場合は、この回路の増幅率はRf/Riです。
一方、周波数が十分高い場合、(1/2πfC)がRfに比べて小さくなるため、並列つなぎ全体で(1/2πfC)になります。つまり、増幅率は(Rf/2πfC)になります。これは周波数が10倍になると、増幅率が10分の1になることを意味します。
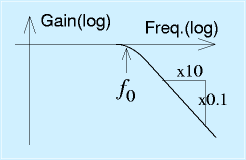 以上を周波数ごとに計算し、両対数でグラフに増幅率gainと周波数freqでプロットすると、右図のようになります。
ほぼ一定の増幅率の区間と、周波数10倍で出力10分の1になる区間の境界のあたりの周波数f0は、計算上、(1/2πfC)=Rfとなる、f0=(1/2πRfC)になります。これをカットオフ周波数とよびます。
以上を周波数ごとに計算し、両対数でグラフに増幅率gainと周波数freqでプロットすると、右図のようになります。
ほぼ一定の増幅率の区間と、周波数10倍で出力10分の1になる区間の境界のあたりの周波数f0は、計算上、(1/2πfC)=Rfとなる、f0=(1/2πRfC)になります。これをカットオフ周波数とよびます。
 逆に入力にコンデンサをいれると、周波数の高い成分を通し、低い成分を減衰させるハイパスフィルタを作ることができます。今度は、抵抗Riとコンデンサのインピーダンス(1/2πfC)の直列つなぎになります。
逆に入力にコンデンサをいれると、周波数の高い成分を通し、低い成分を減衰させるハイパスフィルタを作ることができます。今度は、抵抗Riとコンデンサのインピーダンス(1/2πfC)の直列つなぎになります。
ローパスフィルタのときと同じように、周波数によってRiと(1/2πfC)のどちらが大きいかを考えると(直接接続の場合は、大きい抵抗の抵抗値が支配的)、その特性が得られます。
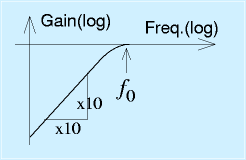 右図はハイパスフィルタの特性です。カットオフ周波数はf0=(1/2πRiC)となります。
右図はハイパスフィルタの特性です。カットオフ周波数はf0=(1/2πRiC)となります。
ローパスフィルタの主な使い道は、ノイズ除去です。一般に、ノイズとされる不要な雑音信号は周波数が高いところに存在します。ロボットに搭載するようなセンサは一般に1[kHz]も反応しないのですが、モータが出すノイズやその他電磁波などは多くがそれよりも周波数が高いところに存在するため、ローパスフィルタを適宜いれれば解決できます。
一方、ハイパスフィルタは主に直流成分を除去するために使用します。センサの出力を数百〜数万倍と大きく増幅したい場合、センサの出力に最初から1V足されたような状態で出力されていると、それも一緒に増幅してしまうことになります。また、オペアンプは実際に使うと出力のゼロ点が若干ずれることがあり、これも問題になることがあります。このような常に加わっている直流の電圧を除去する場合、これまでの方法を使うなら、差動増幅などをつかって引きます。
ですが、この信号の出力で直流分、すなわち静止状態の信号や、周波数の低い=ゆっくりした変化がいらない場合は、このハイパスフィルタをいれてそれらを除去して増幅することができます。
このような増幅の代表例は音声信号です。人間に聞こえる周波数は低くても20[Hz]なので、増幅するときに低い周波数をカットしてもかまいません。また、特定の周波数の計測と限定されていれば、それ以外は除去できます。
このローパスとハイパスを適宜組み合わせると、ある周波数範囲だけを通すバンドパスフィルタがつくれます。
今回の回路では周波数を10倍にすると、増幅率が10分の1や10倍になる傾斜です。これは一見すると大きな変化に見えるかもしれませんが、実際につかうとかなりヌルい特性です。そのため、回路を工夫して、周波数10倍で100分の1、千分の1といった急激な減衰を得る回路もあります。
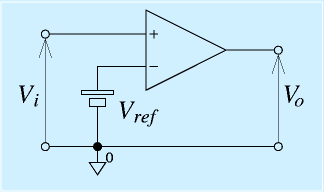
コンパレータ(比較回路)
 これまでの回路は、連続的な値を連続的に処理してきました。しかし、センサ回路をつくるとき、ときとして白黒をはっきりつける必要があります。たとえば、「ある温度を超えたら動作」とかです。
これまでの回路は、連続的な値を連続的に処理してきました。しかし、センサ回路をつくるとき、ときとして白黒をはっきりつける必要があります。たとえば、「ある温度を超えたら動作」とかです。
このような場合に使用する回路がコンパレータです。
回路はこれまでで一番簡単です。オペアンプの+入力に入力電圧をかけ、−入力端子に何らかの比較対象となる電圧Vrefを与えます。ここでは電源を書いていますが、オペアンプの入力は電流が流れないため、たとえば抵抗で分圧したものでもかまいません。
この回路では、入力端子の差を大きく増幅して出力する、というオペアンプの特性上、入力がVrefより大きいと出力は最大値に振り切り、入力がVrefより小さいと最小値に振り切ります。
たとえば、実在のオペアンプを±12[V]で動作させた場合、大きいと出力は10[V]程度、小さいと-10[V]程度になります。
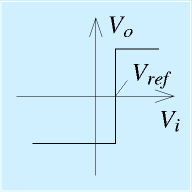 この入出力特性をグラフにすると右図のようになります。
この入出力特性をグラフにすると右図のようになります。
なお、通常のオペアンプでもコンパレータとして使えますが、一般には専用の「コンパレータ」というICを使います。これはオペアンプによるコンパレータに比べて高速応答すること、デジタル回路との接続がしやすいことなどの利点があります。
 コンパレータはその要求に忠実に答えます。ところが、入力に微妙なノイズが乗っていたりすると、入力とVrefが近い場合(たとえば入力が徐々に増えてVrefを超える場合)に出力が激しく変化することになります。
たとえば、「温度がある程度さがるとヒータをオンにする」ような回路では、このぎりぎりのところでヒータが激しくオンオフして、その切り替え部分にもヒータにも良くありません。
コンパレータはその要求に忠実に答えます。ところが、入力に微妙なノイズが乗っていたりすると、入力とVrefが近い場合(たとえば入力が徐々に増えてVrefを超える場合)に出力が激しく変化することになります。
たとえば、「温度がある程度さがるとヒータをオンにする」ような回路では、このぎりぎりのところでヒータが激しくオンオフして、その切り替え部分にもヒータにも良くありません。
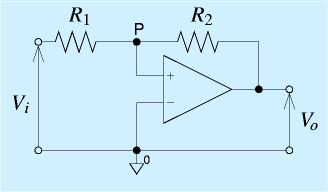
そのようなときに使うのが、右に示すヒステリシスコンパレータです。一見すると反転増幅回路に見えるのですが、よく見ると入力端子が逆になっています。つまり、−端子がGNDに接続され、+端子に入力と出力が抵抗を介してつながっています。
この回路を具体例で見ていきましょう。たとえば、R2=5R1だとします。また、オペアンプの出力は±10[V]とします。
- 入力が徐々に上昇する場合を考えます。出力は-10[V]に最初なっていて、入力が徐々にあがり、+端子が0を超えると、基準をこえて出力が10[V]になります。入力Viが0[V]ではこのラインに到達せず、2[V]になって初めて、+端子が0[V]になります。つまり、入力が2[V]を超えると、出力が-10→10[V]になります。
- 今度はそこから徐々にViが下がります。同じように考えると、入力が-2[V]になってやっと出力が10→-10[V]になります。
つまり、ただのコンパレータに比べて、抵抗比できまるところまで粘ります。逆に、一度切り替わってしまうとちょっと入力が戻ったくらいでは再度切り替わりません。
この回路を使えば、ノイズでこまごまと切り替わることは一般になくなります(この切り替え幅より大きいノイズがくるとこまりますが)。
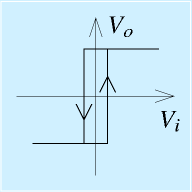
これをグラフに表すと右図のようになります。特徴は、矢印がついているように、電圧の上昇時と下降時で異なる特性をもつことです。
このような行き帰りの違う特性をヒステリシスといい、この回路をヒステリシスコンパレータといいます。
このヒステリシスは現実の世界にはいろいろありますが、制御対象としたり、センサとしては一般に嫌われる特性です。
身近な例では、寒くなってきたときに、しばらく夏服で粘りますけど、あるところまでいくと衣替えして冬服に。その後ちょっと暖かくなっても夏服にはもどしません。逆に、冬が終わりある程度まで暖かくなると(冬服にした温度よりは高い)、夏服に切り替えると思います。これも一種のヒステリシスです。
まとめ
アナログ回路はその回路図集だけで本がかるく数冊できるほど、いろいろな種類がありますが、我々が計測や制御を行う場合には、概ね、ここで示したような回路の組み合わせで済むことが一般的です。
対象となる信号の大きさ、どこまで増幅したいか、どう処理すればよいかを考え、それぞれの部分に切り離し、ここで扱ったような回路を導入し、各部の定数を決める。その上で半田付けして作り上げます。
回路を設計するというと難しそうに聞こえますが、実は、ワンパターンに回路のブロックを選んで、数字を決めるだけの簡単な物、くらいに思っておくといいでしょう。
ただ、アナログの場合は作り方などによってもその性能が変わるため、きっちり性能を出そうとするといろいろと難儀することも確かで、「やってみなけりゃわからない」ところが多いのが難点です。
このページ、ここで終了。
熊谷正朗
[→連絡]
東北学院大学
工学部
機械知能工学科
RDE
[| ]
 オペアンプは「オペアンプ」(Operational Amplifier)と呼ばれる、増幅機能をもった回路です。そのため、必ずしもICの形をしているとは限りませんが、オペアンプというICも多く市販されていて、普段はそれをつかいます。
オペアンプは「オペアンプ」(Operational Amplifier)と呼ばれる、増幅機能をもった回路です。そのため、必ずしもICの形をしているとは限りませんが、オペアンプというICも多く市販されていて、普段はそれをつかいます。 さて、オペアンプ、電源が無ければならないのは当たり前なので、回路図を書くときはしばしば省略されます(回路図の隅の方に、別途電源供給の指示を書くなど)。また、記号の形状から、OUTもわざわざ表記する必要はありません。さらに、入力も、記号の中に+−が書いてあるので、それで十分です。
そのため、一般には右図のような形で書かれます。この講義でも特に明示する必要がない限りこう書きます。
さて、オペアンプ、電源が無ければならないのは当たり前なので、回路図を書くときはしばしば省略されます(回路図の隅の方に、別途電源供給の指示を書くなど)。また、記号の形状から、OUTもわざわざ表記する必要はありません。さらに、入力も、記号の中に+−が書いてあるので、それで十分です。
そのため、一般には右図のような形で書かれます。この講義でも特に明示する必要がない限りこう書きます。![]()
 オペアンプを使った増幅回路で一番基本となる、反転増幅回路を見てみます。
オペアンプを使った増幅回路で一番基本となる、反転増幅回路を見てみます。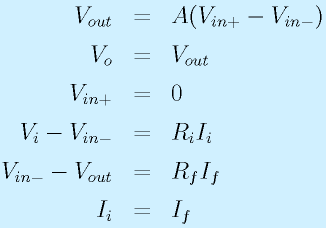
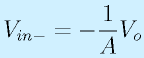
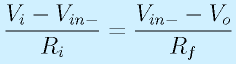
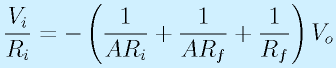
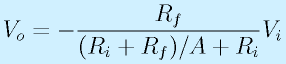
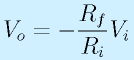
 次に、非反転増幅回路を見てみます。
次に、非反転増幅回路を見てみます。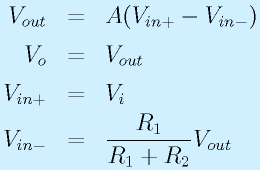
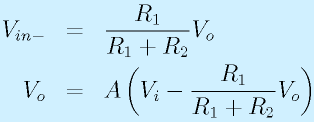
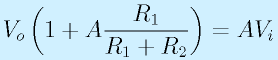
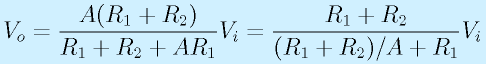
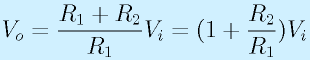
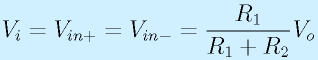
 複数のセンサの出力を合成したり、ある信号に、電圧のゲタを履かせたり(=単純に1V加えるなど)するときに必要になるのが、加算回路です。
複数のセンサの出力を合成したり、ある信号に、電圧のゲタを履かせたり(=単純に1V加えるなど)するときに必要になるのが、加算回路です。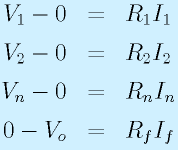
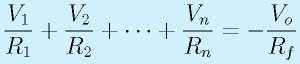
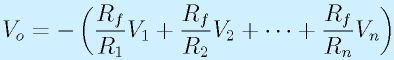
 先ほどの加算回路は加算といいつつ、反転も入っています。
そこで、右の図のように2個つなぐと加算と減算をまとめていろいろ入力できます。
VPの側の入力からは2回反転するので、正負そのまま、VN側は反転します。あとは抵抗値を適宜選ぶことになります。
先ほどの加算回路は加算といいつつ、反転も入っています。
そこで、右の図のように2個つなぐと加算と減算をまとめていろいろ入力できます。
VPの側の入力からは2回反転するので、正負そのまま、VN側は反転します。あとは抵抗値を適宜選ぶことになります。 反転増幅回路の抵抗を一本、コンデンサに変えると積分回路がつくれます。
反転増幅回路の抵抗を一本、コンデンサに変えると積分回路がつくれます。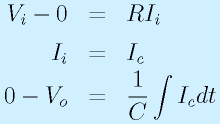
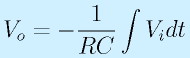
 コンデンサと抵抗の位置を逆にすると微分回路を作ることができます。
コンデンサと抵抗の位置を逆にすると微分回路を作ることができます。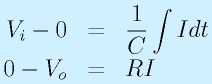
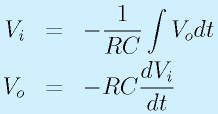
 増幅回路の主な役目の一つは電圧を大きくするという意味の増幅です。
もう一つの意味が、「電圧は変えないけど、大きな電流出力に耐えられるようにする」増幅です。
専門的には「(出力)インピーダンスを下げる」とも言います。
多くのセンサや受動部品(抵抗、コンデンサ)を組み合わせた回路は、それに続く回路で電流を吸ってしまうと特性に影響を受けます。そのため、なるべく電流を流すこと無く、電圧だけを後ろに伝えることが重要です。ですが一般的な用途では電流を吸ってしまう回路が多いため、その間で電流だけ増やす必要があります。
増幅回路の主な役目の一つは電圧を大きくするという意味の増幅です。
もう一つの意味が、「電圧は変えないけど、大きな電流出力に耐えられるようにする」増幅です。
専門的には「(出力)インピーダンスを下げる」とも言います。
多くのセンサや受動部品(抵抗、コンデンサ)を組み合わせた回路は、それに続く回路で電流を吸ってしまうと特性に影響を受けます。そのため、なるべく電流を流すこと無く、電圧だけを後ろに伝えることが重要です。ですが一般的な用途では電流を吸ってしまう回路が多いため、その間で電流だけ増やす必要があります。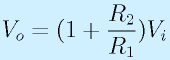
 差動増幅回路は2つの電圧の差をとって増幅する回路です。演算と言うよりは増幅に分類されています。
差動増幅回路は2つの電圧の差をとって増幅する回路です。演算と言うよりは増幅に分類されています。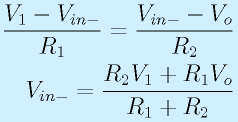
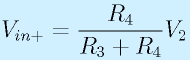
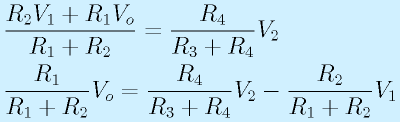
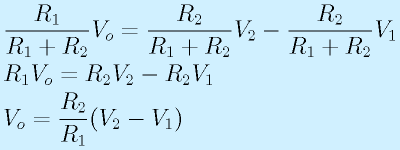
 この差動増幅回路は文字通り差をとることに使えますが、実際のセンサ用途では発展型である次のインスツルメンテーションアンプが使用されます。
この差動増幅回路は文字通り差をとることに使えますが、実際のセンサ用途では発展型である次のインスツルメンテーションアンプが使用されます。 上述の差動増幅回路は大きく二つの問題点があります。
上述の差動増幅回路は大きく二つの問題点があります。
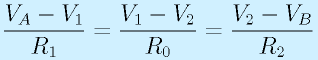
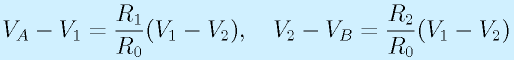
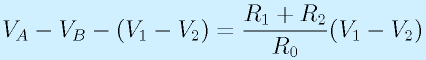
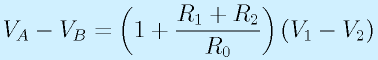

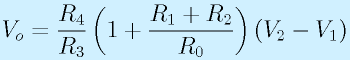
 センサの中には、その出力が電流のものがあります。たとえば光系のセンサは、光量に比例した電流が出力されます。これを電圧に変換し、必要に応じて増幅するものに、電流電圧変換回路があります。
センサの中には、その出力が電流のものがあります。たとえば光系のセンサは、光量に比例した電流が出力されます。これを電圧に変換し、必要に応じて増幅するものに、電流電圧変換回路があります。 相手が電子回路の時には、電流出力で信号を渡すことはあまり多くありません。まれに信号の送受で使われることがあります(電圧は途中の抵抗で減りますが、電流は分岐しなければ減らないため)。電子回路の中では電流源はときどき使われますが(オペアンプ自身の中にもいくつかあります)、普通は一定の電流です。
相手が電子回路の時には、電流出力で信号を渡すことはあまり多くありません。まれに信号の送受で使われることがあります(電圧は途中の抵抗で減りますが、電流は分岐しなければ減らないため)。電子回路の中では電流源はときどき使われますが(オペアンプ自身の中にもいくつかあります)、普通は一定の電流です。 信号を処理する場合に、信号の正の部分だけほしい、もしくは、絶対値がほしい、という場合があります。
信号を処理する場合に、信号の正の部分だけほしい、もしくは、絶対値がほしい、という場合があります。 右図にその回路を示します。反転増幅回路にダイオードが2本追加されています。
右図にその回路を示します。反転増幅回路にダイオードが2本追加されています。 以上まとめると、
以上まとめると、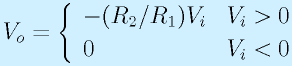
 これを応用すると、絶対値回路を作ることができます。
右のような回路を構成し、R1=R2=R3=R, R4=R5=2Rとします。
これを応用すると、絶対値回路を作ることができます。
右のような回路を構成し、R1=R2=R3=R, R4=R5=2Rとします。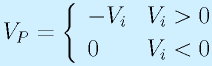
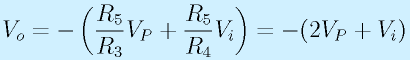
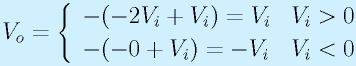
 ここでは、R5=R4=2R3と置きましたが、R4=2R3のまま、R5を変えると、
ここでは、R5=R4=2R3と置きましたが、R4=2R3のまま、R5を変えると、 右図はローパスフィルタと呼ばれる、周波数が低い成分だけを通し、周波数が高くなるほど信号が小さくなるような回路です(もっとも初歩的な構成)。
右図はローパスフィルタと呼ばれる、周波数が低い成分だけを通し、周波数が高くなるほど信号が小さくなるような回路です(もっとも初歩的な構成)。 以上を周波数ごとに計算し、両対数でグラフに増幅率gainと周波数freqでプロットすると、右図のようになります。
ほぼ一定の増幅率の区間と、周波数10倍で出力10分の1になる区間の境界のあたりの周波数f0は、計算上、(1/2πfC)=Rfとなる、f0=(1/2πRfC)になります。これをカットオフ周波数とよびます。
以上を周波数ごとに計算し、両対数でグラフに増幅率gainと周波数freqでプロットすると、右図のようになります。
ほぼ一定の増幅率の区間と、周波数10倍で出力10分の1になる区間の境界のあたりの周波数f0は、計算上、(1/2πfC)=Rfとなる、f0=(1/2πRfC)になります。これをカットオフ周波数とよびます。 逆に入力にコンデンサをいれると、周波数の高い成分を通し、低い成分を減衰させるハイパスフィルタを作ることができます。今度は、抵抗Riとコンデンサのインピーダンス(1/2πfC)の直列つなぎになります。
逆に入力にコンデンサをいれると、周波数の高い成分を通し、低い成分を減衰させるハイパスフィルタを作ることができます。今度は、抵抗Riとコンデンサのインピーダンス(1/2πfC)の直列つなぎになります。 右図はハイパスフィルタの特性です。カットオフ周波数はf0=(1/2πRiC)となります。
右図はハイパスフィルタの特性です。カットオフ周波数はf0=(1/2πRiC)となります。 これまでの回路は、連続的な値を連続的に処理してきました。しかし、センサ回路をつくるとき、ときとして白黒をはっきりつける必要があります。たとえば、「ある温度を超えたら動作」とかです。
これまでの回路は、連続的な値を連続的に処理してきました。しかし、センサ回路をつくるとき、ときとして白黒をはっきりつける必要があります。たとえば、「ある温度を超えたら動作」とかです。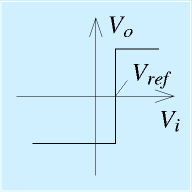 この入出力特性をグラフにすると右図のようになります。
この入出力特性をグラフにすると右図のようになります。 コンパレータはその要求に忠実に答えます。ところが、入力に微妙なノイズが乗っていたりすると、入力とVrefが近い場合(たとえば入力が徐々に増えてVrefを超える場合)に出力が激しく変化することになります。
たとえば、「温度がある程度さがるとヒータをオンにする」ような回路では、このぎりぎりのところでヒータが激しくオンオフして、その切り替え部分にもヒータにも良くありません。
コンパレータはその要求に忠実に答えます。ところが、入力に微妙なノイズが乗っていたりすると、入力とVrefが近い場合(たとえば入力が徐々に増えてVrefを超える場合)に出力が激しく変化することになります。
たとえば、「温度がある程度さがるとヒータをオンにする」ような回路では、このぎりぎりのところでヒータが激しくオンオフして、その切り替え部分にもヒータにも良くありません。 これをグラフに表すと右図のようになります。特徴は、矢印がついているように、電圧の上昇時と下降時で異なる特性をもつことです。
これをグラフに表すと右図のようになります。特徴は、矢印がついているように、電圧の上昇時と下降時で異なる特性をもつことです。