09/05/11 抵抗、電圧、分圧
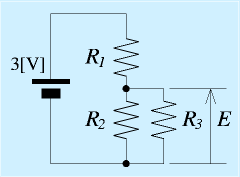Ｑ：右の図において、抵抗R1=200, R2=100[Ω]のとし、R3を以下の抵抗値としたときに、抵抗R2,R3の両端に発生する電圧を求めよ。
・R3=∞
・R3=100[Ω]
・R3=99900[Ω]
Ａ：
○ R3=∞の場合：
無限大というのは、接続していないのと同じなので、この場合はR1,R2による分圧回路になります。
分圧比率は200:100なので、分圧の計算より
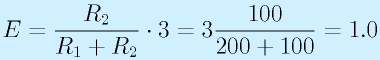
よって、1.0[V]となります。
なお、回路を流れる電流から求める場合、電流は 3/(200+100)=0.010[A]、よってE=0.010*100=1.0[V]となります。
マークは 0-1-0-0-0。
○ R3=100[Ω]の場合：
まず、R2とR3の並列合成抵抗R23を求めます。
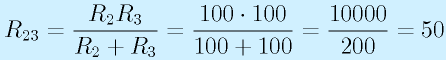or
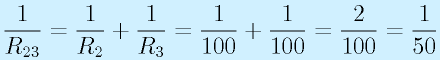
よって、R2,R3の合成抵抗は50[Ω]です。
この50[Ω]とR1=200[Ω]の分圧回路になります。
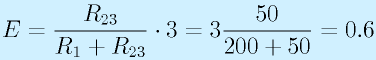
よって、0.6[V]となります。
マークは 0-0-6-0-0。
○ R3=99900[Ω]の場合：
まず、R2とR3の並列合成抵抗R23を求めます。
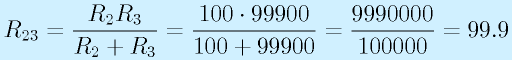
よって、R2,R3の合成抵抗は99.9[Ω]です。
この99.9[Ω]とR1=200[Ω]の分圧回路になります。
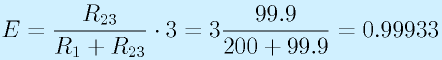
よって、0.9993[V]となります。
マークは 0-0-9-9-9。
解説：
単純な計算ですが、R3の値の変化で電圧が変ることが確認できます。
講義のとき、「分圧」で、「後ろに電流が流れていかないような場合、後ろの抵抗値が十分大きい場合」に、適当な比率の電圧をつくることができると話しました。R3=∞は本当になにも無い理想状態で、200:100なので、1/3の1.0[V]になります。
しかし、後ろに、100[Ω]という、分圧回路を作るための抵抗に匹敵するようなものがぶら下がると、電圧が0.6[V]まで下がります。後ろの回路が純粋な抵抗なら、あらかじめ調整することもできますが、一般にはそう簡単ではありません。
で、ぶら下がる抵抗が 99900[Ω]、約千倍のときは、0.9993[V]と、誤差が1/1000[V]程度に収まります。どのくらいの精度が必要かにもよりますが、一般に、電子回路の精度で0.1%というのは、かなり高い部類で、まあ、100倍もあれば、それほど困らない1%精度くらいにはなります。
さて、では、２番目のケースのように100[Ω]をつなぎたい場合、R1=2, R2=1[Ω]にすればいいのでしょうか？
その場合、R1,R2に流れる電流は1[A]ほどになります。常識的に考えたら、これはかなり無駄な電力です(熱になるだけ)。
そういうときにはまじめに回路をつくることになります(実質的に、出力1.0[V]の電源回路をつくることになる)。
09/06/15 オフセットつき増幅
Ｑ：出力電圧Voが、入力電圧Viによって
と得られるような回路を設計せよ。その際、2[V]等の直流電源を使用してよい。
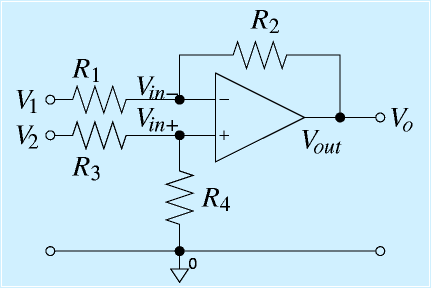Ａ：ヒントでしつこく「引いて増幅」と言っていたように、引く＆増幅の回路を選択します。
ずばり、「差動増幅」回路を使うことができます。
右図において、R1=R3, R2＝R4とすれば、
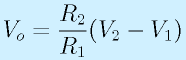
です。なので、R2(R4)/R1(R2)=10 にし、V2=2[V]とします。すると、
となるので、V_1をV_iとすればＯＫです。現実的には、R1=10[kΩ], R2=100[kΩ]程度に選定します。
ただし、要件として、回路図として完成させること、端子や「V1, V2」を残しておかないこと（あくまで入力をViとすること）を求めており、それに反した場合は減点、また、抵抗値としてR2の抵抗値が10kを大幅に下回る場合は減点しています。
Ａ２：別解１
加減算回路をつかうこともできます。が、オペアンプも２個になり、回路も面倒になるので、よい設計、ではなくなります。
Ａ３：別解２
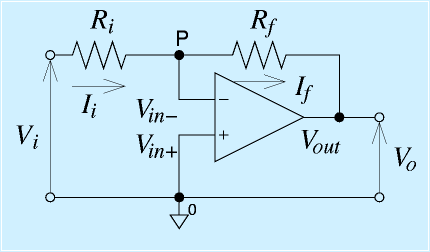
ただの反転増幅回路を使う方法もあります。
右図、反転増幅回路で、Vin+をGNDではなく、適当な電圧Vrにつなぐとします。
その際、仮想短絡により、
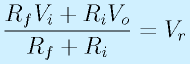
となります。これを解くと
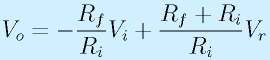
となり、10倍にするには、Rf=10Riとします。
1.1Vr=2.0[V]になるような電源を用意すれば、目的の増幅ができます。
この方法は、
１：抵抗２本でできる
２：Vrはオペアンプ(-)端子のみにつながっている＝電流は流れない(c.f.↑Ａではただの差動増幅で電流が流れる)ので、可変抵抗で分圧した電圧でよい＝簡単に調整可能な電圧
という特徴があり、案外、調整が前提なセンサ信号の処理とかで便利です。
ただ、あとで何の回路かわかりにくくなるので、試作回路向きではありません。
よくみると、差動増幅回路のプラス側を固定したもの、とも見えます。
Ａ４：別解３
プチテストの解答の中にあった「理論上は可能な」方法です。
なので、「Viから2V引いて」「-10倍の反転増幅」することにして、
Vi--[-2V]--反転増幅(10倍)
と、-2Vの直流電圧源を直列に接続してしまいます。
回路図の上では可能ですが、この[2V]は増幅回路や入力される信号とはまったく独立して2Vを保つ必要があります。
たとえば、電池はそのような性質をもっていますが、ジャスト2Vの電池はありませんし、適当な電池を抵抗で分圧して使うわけにもいかず、実現は面倒です。
（この目的ではありませんが、絶縁型電源回路、なるものをもちいて、電圧の下駄を履かせる、という手法自体は、実用的に存在しています。）
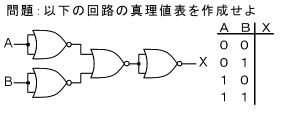
090718 真理値表を求める
 |
 |
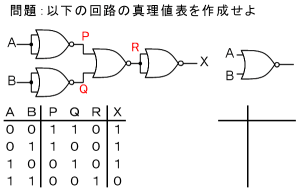Ａ：
入力のすべてのパターンに対して、Ｘがどうなるかを確認していくだけの問題です。
途中の配線にも適当な記号を付け、それらを入力から順に落ちついて追っていけば簡単に求まります。
ちなみに、これはNORをド・モルガンすると、NANDになることを示しています。