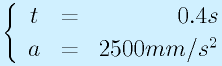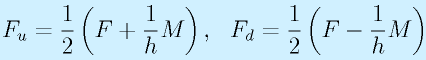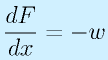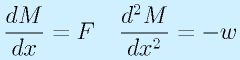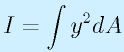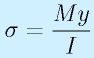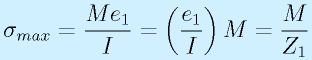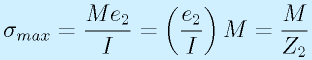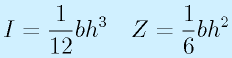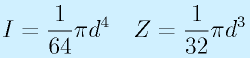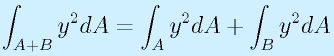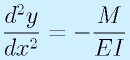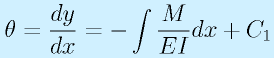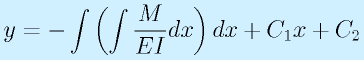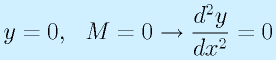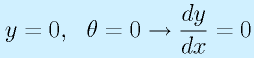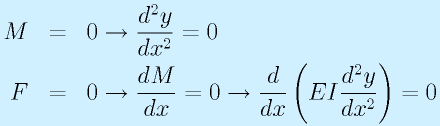機械的な検討
[| ]
最終更新: 2018/04/17 19:24:12
ロボットの構造を考える
 |
| 直交座標型ロボット1 |
 |
| 直交座標型ロボット2 |
 |
| SCARA型ロボット |
 |
| 車輪移動型搬送ロボット |
まず、検討するロボットの仕様をもう一度確認します。
- 物体は直径40[mm]×高さ40[mm]、質量400[g]
- 搬送の領域は直方体空間とし、幅300~2000[mm]、奥行100~2000[mm]、高さ100~300[mm]
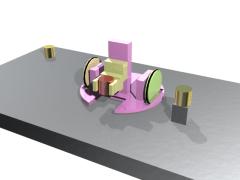
ものを運ぶ機構として、簡単なものに右図のようなものがあります。
(これらはあくまで構造が分かるようにした模式図なので、このまま実用になるものではありません)
図の解説:
- 灰色の台が物体を運ぶ空間のスペース。本来は、ここに搬送物をさらに取り扱う機器類があったりする。
- 金色の円筒(2個)は物体搬送の始点と終点。1個は台の上に直に、もう1個は小さな箱の上に乗っている(=高さが高い位置)
- ロボットの構造部において、
青の部分:土台として据え付ける場所。強度は十分あると考える。
紫の部分:リンク0(→ロボット基礎工学:マニピュレータ)=ロボットの基礎部分、ただし車輪移動ロボットに限り、ロボットの車体
薄橙の部分&黄緑の部分:リンク1とリンク2(車輪ロボットは車輪)
黄色の部分:リンク3、エンドエフェクタ(物体を把持する部分)
それぞれのロボットの解説
(動画にはWindowsMediaVideoの再生環境が必要です)
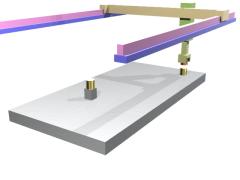
- 直交座標型ロボット1
長手方向に直動の駆動ユニットをおき、その上に柱を立てて横にはりをだし、もう一方の水平方向の動きをつくる。
最後に上下の直動ユニットで手先を上下させる。
もし、対象に対して、真上からのアプローチが必要ない場合、むしろ水平からのアプローチが必要な場合は、垂直の柱部分に上下動のアクチュエータをいれ、3つめを奥行き方向のアクチュエータとしたほうが、構造的には簡素化する。
当然、奥行きの深い用途には向かない。
直交1 400x300 (2018/04/17, 768,889 bytes)
直交1 640x480 (2018/04/17, 1,386,489 bytes)
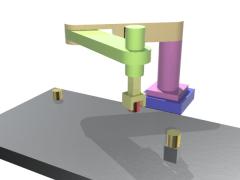
- 直交座標型ロボット2
工場内全体を動くクレーンなどに見られる機構で、リンク1のはりを両端で支持するためにある程度の長さまでは実用的に使える。
身近なところではUFOキャッチャーがこの型。
強度は出しやすいが、レールが左右に2本必要なので、その並行度や、斜めになることなく動かすための工夫など、片持ち構造に比べて気を遣うこともある。
直交2 400x300 (2018/04/17, 682,489 bytes)
直交2 640x480 (2018/04/17, 1,165,689 bytes)
- SCARA型マニピュレータ
※SCARA=Selective Compliance Assembly Robot Arm
水平方向にしか曲がらないマニピュレータの先に上下動する部分をつけた構造。
直動ではなく、回転関節を使うため、構造的にシンプルである。
また、直交座標型に比べて比較的コンパクトになる。
ただし、手先位置の計算には三角関数が必要となる(コンピュータが計算するので問題は皆無)。「手の届く範囲」の検証にも注意が必要である(特に、関節を曲げられる角度範囲)
また、結局片持ちなので、遠くまで届かせるには、強度が問題になってくる(ただし、軸がすべて垂直軸であり、多軸のマニピュレータに比べると関節トルクで加重を受けない分だけたわみにくい)。
このSCARA型というタイプは、産業用の生産設備などでかなり使われている。
SCARAマニピュレータ 400x300 (2018/04/17, 583,289 bytes)
SCARAマニピュレータ 640x480 (2018/04/17, 986,489 bytes)
- 車輪移動型搬送ロボット
移動対象の周囲が平坦で、かつ、比較的広範囲で搬送する必要があるときは、車輪移動型がコンパクトに、低コストに実現できる。
基本的に地面に接地しているため、把持のアームを変にのばしたりしなければ安定性も高い。
移動方法も様々な経路がとれる。
ただし、車輪が滑ると位置がずれることが最大の弱点。そのため、路面にラインを引いてそれをたどったり、周囲の物体、マークなどを認識して補正するための仕掛けが必要。
ラインをたどる手法は古くから実用化されている。
電源については、ある程度動きが限定されるなら有線供給が考えられるが、一般には充電池を使う。工場などで使用するには、自動での充電手段が必要となる。
車輪型搬送 400x300 (2018/04/17, 887,289 bytes)
車輪型搬送 640x480 (2018/04/17, 1,620,089 bytes)
上記ロボットのモデル/モーションデータ(Shade 10.5) (2009/04/21, 1,557,621 bytes)
この方法で全部OKという方法があればいいのですが、やはり目的に応じて「より適切な」構造があります。
実際の工場でも、単に1直線上を運ぶだけなら、直動のモジュールを2個組み合わせて、水平動+垂直動をつくって運びます(軽いものならエアシリンダーなども使われる)。
多少複雑な移動経路が必要だったり、条件(良品/不良品)で仕分けたりするときには、動作をプログラムしたSCARA型ロボットが使われていますが、コスト的には高くなります。
実際の現場では「任意の運搬」が必要ということは普通はありません。その意味で、現実離れはしていますが、指定の領域で搬送を行うロボットを考えてみましょう。
今後、そのロボットのアイデアに基づいて、力の見積や、強度計算、制御方法などを考えていきます。
レポート1
別途指定された空間でものを運搬できるロボットを上の4例をもとに検討してください。
検討結果は、なるべくリアルに(構造が分かるように&寸法比が正確なように)、図面やイラストの形にまとめてください。
その際、検討の経過はノートにまとめておくこと。今後のレポートの下地になります。
なお、「実際につくるわけ」ではないので、それほど無謀なアイデアでなければ、かまいません。
その結果、計算値があり得ないことになるかもしれませんけど、それもまた経験です。
ただし、一度選んだら、この講義の終了まで責任を持ってもらいます。
ロボットに作用する力1
ロボットに直接的に作用する力
ロボットに作用する力は数え上げればきりがありません。
目立つところでは各部に作用する重力があり、その重力が片持ち・両持ちはり構造のロボットにのしかかり、曲げモーメントになります。
曲げモーメントは軸受けに働く力になったり、モータで駆動するトルクになったり、なにより「構造的に壊れないのか?」というチェックに必要だったりします。
まずは、ロボットの内部の細々とした力のやりとりではなく、おおざっぱに「外から見て分かる」直接的に作用する力を考えてみます。
ロボットに作用する力で直感的に思い当たるのは以下の3種類です。
- 各部に働く重力:
地球上では、言うまでもなく、ものには重力が作用します。
搬送する対象はもちろん、ロボットを構成する各部品にも発生します。
ロボットの構造によっては、搬送対象に働く重力よりも、ロボット自身の自重のほうがずっと重荷になることもあります(たとえば、「お姫様だっこ」は鍛えてないと普通はできない:自重ぶんだけ抱えて運べない)。
- 作業対象に作用する(させる)力:
運ぶだけなら、おもに重力、慣性力ですが、組立ロボットや機械加工ロボットの場合、押しつけたり引っ張ったりするための力が別に必要になります。
下向きの組み付けであれば、ロボットの(部分の)自重が使える可能性が高く、自分を支えられるだけの強度出力があれば十分ですが、上向きに押しつけようとすると自重+押しつけ力が必要となります。
そのため一般には上向きに押しつけるような組立は避けたほうがいいでしょう。
横向きの場合はケースによります。
- 慣性力:
ものを加速的に動かす場合には慣性力が作用します。
並進の動きに対しては、いわゆる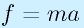 の力が、回転軸周りには
の力が、回転軸周りには のトルクが作用します。
のトルクが作用します。
移動するためには加減速が必要で、それなりに俊敏な動きをするには大きな加速度が必要となります。
それと関連して、力×速度=動力も重要な要素です。そのため、「俊敏な」は二重に影響してきます。
以下では、以上のうち、重力と慣性力について考えていきます。
これらを求めるには、ロボットの質量(重力、慣性力)、慣性モーメント(慣性力)、運動パターンの見積が必要となります。
概略の計算方法
まず、重力の計算の方法ですが、
重力による力=mg (mは質量、gは重力加速度)
なので、さしあたりロボットの質量を見積もる必要があります。
逆に、ロボットの各部の質量さえ決まれば、おしまいです。
つぎに慣性力ですが、
慣性力=ma (aは加速度)、=I d2θ/dt2 (Iは慣性モーメント,d2θ/dt2は角加速度)
なので、並進については質量と加速度、回転については慣性モーメントと角加速度を見積もる必要があります。
慣性モーメントについてはロボットの各部の概略の質量が分かれば、「多めに=安全側」そこそこ手軽にに見積もることは可能です。
加速度、角加速度については、別途、運転の「速度パターン」を想定して計算(決定、仮定)する必要があります。
さて、「ロボットの各部が決まれば質量は求まる」は確かなのですが、大きな問題点があります。
「ロボットの質量」→力、トルク→モータの出力決定、構造材の強度計算→ロボットの構造や材質決定→「ロボットの質量」
ある意味、決まらないのです。
最悪のケースでは「重いから強化したら、また重くなった」というスパイラルに陥ります。
そういうときは、どこかで「えいや」と決めてしまう、構造や材料を工夫しておなじ質量でもより強度を増したり、同じモータでも動きやすくする、そもそもロボットの構造を改める、といったことが必要になります。
いずれにせよ、これらの計算を繰り返し行えることがロボットの設計には必要です。
慣れると、直感で「こんなもん」と決めて、その上で「OKかどうか」のチェックのために計算しますが、足りなければ壊れ、多すぎれば無駄でむやみにコストが高くなる、という危険性は常にあります。
質量の見積
 |
| 角パイプの質量 |
質量の見積はおおむね二つに分けられます。
- 構造材←強度設計などにより決定される
- 駆動装置などのメカ部品(モータ、減速機、回路、バッテリーなど)←部品選定(カタログに質量は記載されている)
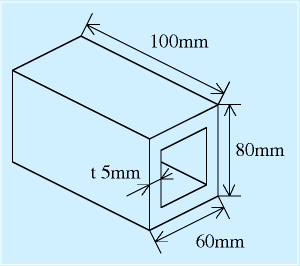
後者は部品を決めたらきまるので、前者の構造材について右の図をもとに試算してみます。
例:角パイプ
長さ100mm、断面は縦80mm、横60mm、肉厚は5mm。
※本来はSIで計算すべきだけど、この計算だけは昔ながらのcm単位が便利※
断面積=8x6-7x5=48-35=13cm2
体積=13x10=130cm3
ここで材質をアルミ系(アルミやジュラルミン)とすると、密度は約2.7g/cm3なので質量350g/長さ100mm程度、鉄系の7.9g/cm3とすると、1kg/長さ100mmとなる。
この程度の長さなら大きな違いに見えないかもしれませんが、長さ1メートルのアームなどをつくろうとすると、10kgになってしまい、かなり重くなります。もちろん、鉄を使うなら、普通はこんなに肉厚にすることはないので、非現実的な例ではあります。
なお(1)、この角パイプ断面を横長ではなく縦長に置いている理由は分かりますよね?
なお(2)、案外見落として罠になるのが「ねじ」です。ネジの質量は1個1個は小さくとも、数が多くなるとバカになりません。
慣性モーメントの見積
 |
| 慣性モーメントの計算 |
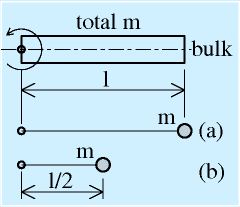 |
| 腕部品の慣性モーメント計算 |
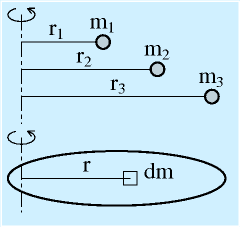
慣性モーメントの計算の定義式は、右の図のような質点の集合や剛体(連続体)に対して、
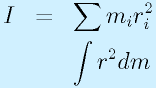
となります。回転軸からの距離の2乗を部分の質量にかけたものの総和です。
ロボットの慣性モーメント見積としては、
- 構造材(はりなど)→連続体と考える
- モータ、減速機などの部品→質点とみなす
でよいでしょう。もちろん、モータや減速機にも大きさはあり、ロボット内で相対的に大きさを占める場合は、連続体として見積もる必要があります。
なお、それらの部品の個々の重心周りの慣性モーメントがIg、質量がmで、回転軸からの距離がrgなら、
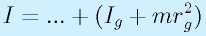
と加えればOKです(逆に、質点と見なす場合はこのIg=0と見なしていることになる)。
右の連続体(直方体形状、長さl、質量m、太さは無視)で計算してみます。計算式にある微少部分の質量dmは、軸からの距離方向rの微少区間drの質量と考えると、(dr/l)mになるので、
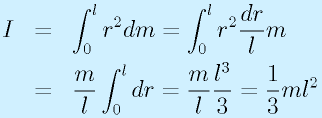
と計算できます。
あえて手を抜いて、この棒を一つの質点としてみてみます。
まず、単純に重心位置、すなわち軸からl/2のところにあるとすると、
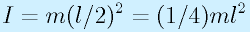
となり、本来の(1/3)ml^2よりも多少小さくなります。誤差と見なせなくもないですが、安全の観点からすると問題です。
一方、質量が、一番遠いところに集中していたと考えると、ml^2になります。これは3倍大きい値なので安全ですが、過剰すぎる可能性があります。この程度の簡単なものははしょらずにちゃんと計算した方がいいでしょう。
なお、慣性モーメントはあちこちに典型的な形の計算法が記されています。これを、先の重心周り→距離ずらしの式で動かしながら加算していくのが現実的には簡単です。
また、3次元CADを使うと、素材を指定すると複雑な形でも一発で質量共々出してくれたりします。
メカの見積
 |
| モータの設置位置(1) |
 |
| モータの設置位置(2) |
直感やこの先の計算で大まかな必要トルク(力)、速度が求まったとします。
そこから、また別の計算に基づいてモータや減速機の選定を行います。
選定により、最低限、カタログから質量(重量と書いてあることが一般的)が得られます。
- ロボットの全体質量にはただ加える
- 慣性モーメントはmr^2で加える
さて、この軸からの半径、を決めるにはモータの設置場所も決めなければなりません。
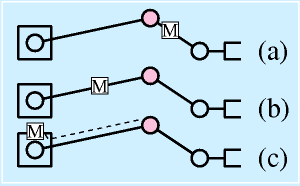
右の図のように、モータの位置はいろいろ置き場所が考えられます。
腕型のロボットにおいて、ピンクで示した肘の関節を駆動するモータはどこに置けばいいでしょうか。
(a)関節の先 (b)関節の手前 (c)ロボットの根本
関節の先に置くと、根本から遠くなると同時に、単純に肘関節で駆動すべき質量、慣性モーメントが増えるため、不利です。腕を高速化する際には根本にモータなどを置いて、ベルトなどで関節まで動力を伝える方法がありますが、この場合、動力を伝える機構の設計が増えます。
とくに多自由度の場合は複雑化し、逆にガタなどで精度が落ちる可能性もあり、(c)がベスト、とも言えません。
よほどスペース的に無理、などでなければ、(a)だけは避ける、が基本です。
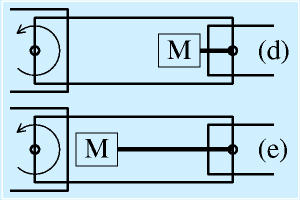
同様に、おなじ(a)関節の手前 に置くとしてもモータを
(d)前の関節の直後に置く (e)駆動する関節のそばに置く
の選択があります。単純には、前の関節の駆動にかかわる慣性モーメントを減らすために(e)が無難ですが、これも短いとはいえ動力伝達が必要なので要注意です。伝達機構の搭載のために質量や慣性モーメントがやたらと増える設計をしたら無駄ですので。
加速度の見積
慣性力を求めるには、あと加速度が必要です。
加速度は目標とする運動=速度パターンを決めれば、そこから計算できます。
ここでは台形加減速を例に実際の計算をしてみます。
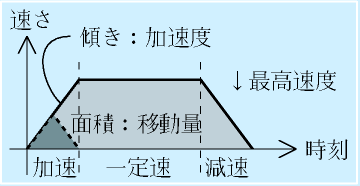
台形加減速は、運動させるときに、速度や角速度を右図のような、時間−速度グラフで台形状になるような運動です。
最初に一定加速度(角加速度)で加速し、その後一定の最高速度をとり、最後に一定加速度で減速します(加速時と減速時の加速度は等しくなくともよいが、ここでは等しいとする)。
この台形の底辺の長さが運動に要する時間、台形の面積が総移動量になります。
なお、移動距離が短い場合は最高速度まで上がらない三角になります。また、この運動は直線運動でも回転の運動でも同様に使われます(ただし、回転で台形加減速すると、手先の速度も加減速するものの、手先座標の運動は台形にはならない)。
実際に計算してみます。
加速部分のみを考えて、加速度a(角加速度ならd^2θ/dt^2)で加速したとすると、時間がt経過したところで速度はat、移動距離は(1/2)at^2になります。
たとえば、200mm移動したところで最高速度1000mm/sになるような運動を仮定すると、
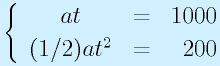 →
→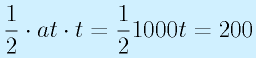 →
→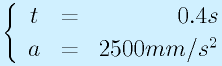
となります(aは重力加速度の約1/4)。
この数値をつかって、2000mm移動することを考えます。
最初と最後の200mmは加減速に使われ、各々0.4sかかります。
中間の一定速度部分は1000mm/sで残りの1600mmを移動するので1.6sかかります。
よって、合計で2.4sが必要になります。
単純に等速なら2sとなりますが、加減速のためにより長く時間がかかります。
よって、往復動作をロボットにさせようとすると、単純に距離/1往復あたりの時間で出した速度よりも性能が必要になります。
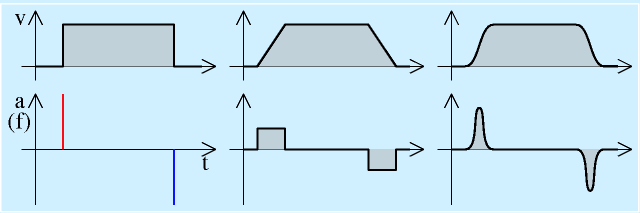 |
| 加減速の種類と加速度 |
さて、この加減速の意義、種類について、右の図で見てみます。
最初の例は加減速動作なしです。ただし、動作制御の「加減速」は「意図的に調整された加減速」を意味し、それがなくとも、当然現実には加減速があります。
この場合、速度の微分値としての加速度は、計算上は無限大になります。
実際に無限大にはなり得ないので(駆動力は無限ではない)、制御の遅れなどの問題を起こしつつ、装置の限界で加速することになります。
次の例は台形加減速です。この場合、傾き一定の区間が、加速度一定の区間となり、装置に要される慣性力はこれに比例した力となります。
最後の例は、より滑らかな関数を使った例です。2次関数(以上の多項式)をつないだものや、正弦波関数を用いたものがあります。当然、上記のような計算はより複雑になります。
この両者の違いは、加速度の波形に出てきます。ロボットなどにいきなり加速度をかける、ということはいきなり慣性力をかけるということです。車でたとえればいきなりアクセルやブレーキを踏むことに相当し、乗り心地が悪くなります。
機械にいきなり力をかけたり抜いたりすることは、一般には振動の原因になりますし、もしも装置にガタがあると、いきなりぶつけることになります。
台形加減速があれば、加減速操作がないのよりはずっと無難ですが、より滑らかな加減速が要求される場合もあります。
なお、同じ時間で同じ速度まで加速しようとすると、当然滑らかにしたほうが、ピークの加速度=ピークの力は高くなります(加速度の面積が速度になる=細長くなるため)。
レポート2
前回のレポートで検討したロボットに対して、ロボットの各部に作用する力を検討してください。
ロボットの概略図の上に矢印などで図示すると共に、その具体的な説明と大きさを述べてください。
大きさについては、算出方法を必要な仮定と共に述べてください。
最終的に、とんでもない計算結果になるかもしれませんが、あまり気にせず、「計算してみること」の意義を優先して、やってみます。
今回実現不可能な数値がでたら、次におなじ設計をしなければいいので。
ロボットに作用する力2
前節では、ロボット全体におおざっぱに作用する力を見てみましたが、ここでは、ロボット設計時に考える必要がある、局所的に作用する力を2種類考えてみます。
摩擦力
システム全体を見たときに「ない方がいい摩擦力」と「必要な、大きければ大きい方がいい摩擦力」があることは容易に想像がつきます。
- 必要な摩擦力: 車輪、物体の把持
車輪で走行するためには、車輪(タイヤ)と路面の間の摩擦力が必要
ものをハンドなどで把持する(つかむ)には摩擦力が必要
- ないほうがいい摩擦力: 機構の運動するところ
摩擦があると、駆動のロスとなる。(伝達効率の低下、発熱など)
逆可動性(出力側を動かしたときにアクチュエータが回るか)が悪化/無くなる
逆可動性は耳慣れないかもしれません。
普通に駆動するときは、モータを回して腕が動けばいいだけに思えますが、何かあったとき、たとえば停電で電源が落ちた、非常停止した、という場合に、自分では動かなくなったロボットを外力で動かすためには、この逆可動性が必要です(研究用ロボットの分野ではわりと重視される)。
※もちろん、電源を切った瞬間に腕が落ちるというのも困るということもあり、その場合は逆可動性を敢えてなくすか、逆可動性は活かしつつ、電磁ブレーキをつかって、電源が落ちるとブレーキするようにします(外力で動かしたいときはブレーキだけ解除)。
実際にロボットを開発するとき、摩擦は見落としがちでありながら、全体の性能にかなり影響するので、以下、詳細を見てみます。
摩擦力の検討
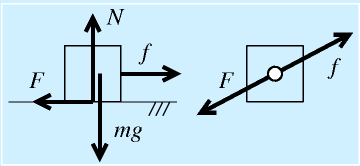 |
| 摩擦力のモデル |
摩擦力F(の最大値)は以下の式で表されます。
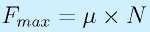
μ:摩擦係数((静摩擦係数、動摩擦係数)
N:垂直抗力(面から垂直に作用する力)
摩擦力で重要な点は、
- 動こうとすること、動きを押さえる方向に働く
(静止物については、外力をかけているのと逆向き、運動中の物体については速度と逆向き)
- 静摩擦については、上式の計算値はあくまで「最大値」
(外力をかけていなければ、摩擦力はゼロ。最大値以下の外力であれば外力と同じ、外力のほうが大きいと、摩擦力は上式)
ということです。よく考えれば当たり前ですが、いくら摩擦係数と垂直抗力から値が求まるからといって、その値が常に作用していたら、止まっているものも動き出してしまいます。
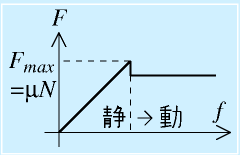 |
| 静摩擦と動摩擦 |
摩擦力には相対速度ゼロのときに働く静摩擦と、こすって運動しているときに働く動摩擦があります。
一般に、動摩擦のほうが静摩擦よりも小さく、一定の力がかかっているものが滑り出したら止まりません。
右の図は静摩擦と動摩擦の関係を表しています。
徐々に力fをかけていくとすると、静止しているうちはfと逆向きに、fと同じ大きさの静摩擦力Fが生じます。
大きさとしてはF=fです。
ただし、静摩擦の限界(=μN)に達すると(f-Fの外力によって)動き始めてしまいます。
すると、Fは動摩擦力に移行し、最大値Fmaxよりも下がり、動摩擦係数×Nになります。
また、摩擦の方向も運動の逆方向になります(力の方向を変えずに動かしている場合は方向に変化がありませんが)。
次に、典型的な摩擦力の例を示します。
| モデル図 | 説明 |
|---|
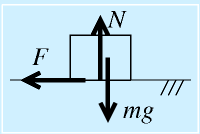 |
水平面上に物体がある場合。
垂直抗力は重力による、面の反力(厳密には、物体の面にも路面にも双方に垂直抗力は働く)。
最大の静止摩擦力は
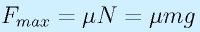
となる。動摩擦力の場合も式の形は同様。
|
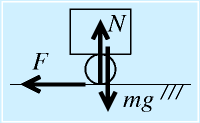 |
車輪に関わる摩擦。
車輪と路面の間に発生する摩擦力は、上記と同じ。
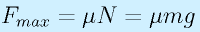
駆動輪の場合は、車輪を回す力がFmaxを超えなければ、安定して推進できる(超えて動摩擦になるとドリフト状態)。
従動輪の場合は、車輪が自由に回る、つまりf=0に相当するので、進行方向の摩擦力は本来生じない(軸受けの抵抗などを無視すれば。また、軸方向には摩擦力は生じうる)。ただし、物体が転がるときには「ころがり摩擦」と呼ばれる僅かな摩擦力が生じる(普段はほとんど無視できる)。
車輪移動ロボットを加速度aで加速しようとすると、加速の慣性力はmaとなり、滑らないためには
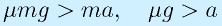
となる。よって、ロボットの加速度はμ(とg)によって制限される。
ちなみに、μは乾いていれば1.0を超える場合もあるが、潤滑すると0.2を切る。
|
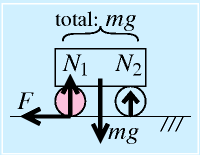 |
車輪が複数有り、駆動は一部の車輪のみの場合。
車輪に生じる垂直抗力は、その合計値が、自重mgになる。
しかし、車輪で駆動する場合、上記計算の摩擦力は、駆動輪の垂直抗力分のみになる。
左図では、N2は関係なく、N1だけになる。
そのため、実現できる加速はμgには及ばない(N2の分目減りしている)。
つまり、「駆動輪にかかる自重」が非常に重要になる。
|
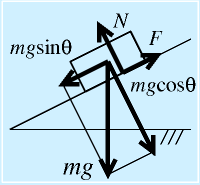 |
斜面における摩擦力。
典型的な問題。斜面の水平からの角度をθとすると、
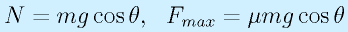
なので、これが坂を下る方向の重力分力よりも小さければ滑らない。
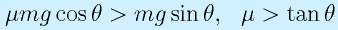
車輪で坂を登るという場合も同様である(mgcosθは駆動輪のみの垂直抗力の計算になり、mgsinθはそのままであることに注意)。
ただし、移動体の場合はこれに加減速に必要な慣性力も加わるので要注意。
|
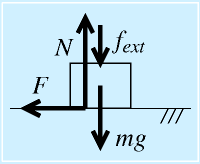 |
押しつけ力による摩擦力の向上。
摩擦係数には限度があり、自重ではまかなえない摩擦力を必要とする場合に、自重に加えて外力でさらに押しつけることが解決策となる。
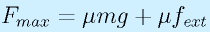
たとえば、F1のレースカーは羽根をとりつけることで、流体力学的に路面に押しつける力fextを発生させて、摩擦力を増し加減速やカーブでの遠心力等により耐えるようにしている。
ロボット競技として有名な相撲ロボットやマイクロマウスでも、ファンを取り付けて路面を吸引したり(車体下部の圧力を下げて大気圧で押しつけるとも言える)、強力な磁石で床面の鉄板に吸い付けたりして、摩擦力を増やしている。
|
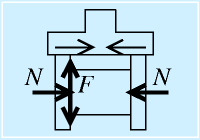 |
ハンドの場合。
両側から、力Nで挟むとすると、摩擦力は、
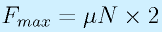
となる。両側から挟む場合、その力は等しいはずで、両サイドで×2となる。
ただし、μには限度がある(ハンドと対象物両方で決まるもので、対象物に依存する)。
また、Nも壊れやすいものなどの場合にあまり大きくできない場合がある。
そのため、実際の仕様に基づいて精査し、左右からのはさみではなく、下からの掬い上げのような、摩擦に直接頼らない方法を検討する必要もあり得る。
|
このように、摩擦力の一部の例だけでも多様で、パターン化も困難です。
- 静摩擦は垂直抗力×静摩擦係数が「最大」でその他の滑らせようと作用している力に逆向きに。
- 動摩擦は運動の方向と逆向き(減速する向き)に垂直抗力×動摩擦係数
という原則をもとに、都度、考えた方がいいでしょう。
現実的な設計では、静摩擦と動摩擦を行き来するような状況は避けるべきです。
あくまで、静摩擦で十分耐えられるか、十分に小さい摩擦力にして抵抗を避けるか、のどちらかを求めるべきです。
可動部の軸受けに作用する力
ロボットを形作るとき、ひとかたまりであるリンク(剛体)を回転や直動の関節でつないだ構造になります。
広い意味では、車輪移動ロボットの、車輪を支える軸と、それを本体に押さえるための軸受け部分も回転関節の一種です。
このような回転関節を支える場合には、一般に軸受けが用いられ、特に滑らかな回転が必要な場合はボールベアリングなどが用いられます。
当然、ロボットにかかる荷重は、この軸受けが支えることになります。
軸受けには許容加重があり、当然、設計するときの選定基準です。
つまり、軸受けに作用する力の見積もりも必要です。
それと同時に、設計の選択肢があるときには、軸受けの負担を小さくするように設計する必要があります。
ここでは、車軸とSCARA型ロボット的な回転関節の軸受けを例に、具体的な計算方法を紹介します。
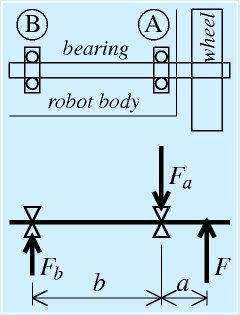 |
| 車輪移動ロボットの車軸 |
車輪移動ロボットの車軸:
ロボットの駆動輪を支持する場合は、車輪に固定した軸をベアリングなどで支えます(従動輪なら車輪にベアリングを入れればよい)。
この車軸を支えるベアリングにかかる荷重を検討します。
右図のように、車軸をロボット車体内のベアリングA,Bで支えます。
車輪には、車体を支えるための力(床からの抗力)Fが作用し、これによって、ベアリングA,Bに力Fa,Fbが作用しているとします。
また、ベアリングと車輪の間隔を図のようにa,bと定めます。
力のつり合いから、
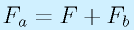
A点周りでのモーメントのつり合いから、

これらを解くと、

となります。
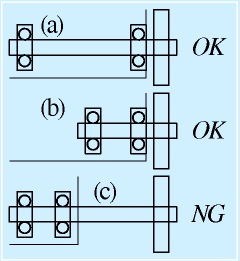 |
| ロボットの車軸:設計案の可否 |
この結果を検討します。大きさは、Fa>F>Fbとなり、Faが大きいことが分かります。
また、どのくらいFより大きくなるかは比率a/bによります。
つまり、車輪よりのベアリングは、支持している荷重より大きな力が作用します。
また、aを小さくすることで、その割り増し分を低く抑えることができます。
逆に、aを大きく、bを小さくすると、Faがかなり大きくなる可能性があります。
そのため、右図のうち、(a)と(b)は妥当な案と言えますが、(c)は明らかにベアリングへの負担が大きく、よほどの事情がなければ採用しない方がいい案です。
もちろん、数字の上では、(b)より(a)のほうがAにかかる力は小さくなりますが、全体的に大きくなる=質量がかさんでコスト高になる=可能性が高いので、計算で確認して、ほどほど、が現実的と言えます。
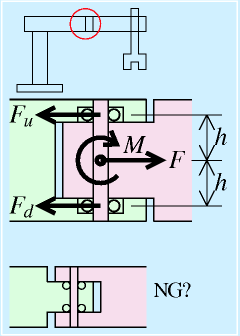 |
| 水平関節ロボットの関節軸 |
SCARAロボットの関節のような水平旋回関節:
水平関節型ロボットの関節のいいところは、関節を駆動するためのトルクに、ロボットの腕にかかる重力が含まれないことです。
トルクは腕の運動のみのため(つまり慣性力のみ)だけを想定すれば良く、比較的小さくて済みます。
一方、対象物、関節から先の腕の自重などは、関節のメカで支えます。
この検討をしてみます。
右図のように、根本に近い側(薄緑)で、先端側(ピンク)を挟むように構成します。
シャフトは先端側に対しては固定していて、そのシャフトを根本側でベアリング支持するとともに、何らかの機構で駆動します。
先端を引っ張る方向に力F、自重等により、腕を下に曲げる方向に働くモーメント(材力のモーメントと同義)をMとします。実際には、これに腕を下に下げる方向(軸方向)の主に重力による力が作用しますが、とりあえず無視します。
このFとMを軸受けにかかる力FuとFdで支えます。
釣り合いより、
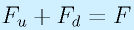 (力のつり合い)
(力のつり合い)
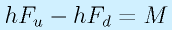 (モーメント、中点周り)
(モーメント、中点周り)
ここで、軸受け間の長さを2hとしています。
これを解くと、
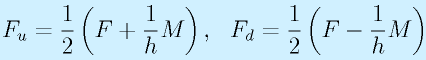
となります。
一般にこのFはあまり大きくはなりません。水平方向に押しつけたり、振り回すことによる慣性力が主要因です。
一方、Mは明らかに影響が大きそうです。
そのため、Fdはマイナスになる可能性は大きいでしょう。つまり、図とは逆に右方向に押す力です(なにか物を自分で上下で持ってみればすぐに分かりますが)。
さて、このFu,Fdを低減するにはどうすればいいかと言えば、Mを小さくするか、hを大きくするかです。
前者は軽量化によって、後者はなるべく軸受けの間隔を広くすることで対応します。
もっとも、軸受けの間隔はロボットの腕の縦幅以上にはなりません。その中で軸受けをなるべく離します。
そのため、下のように、「先端側で上下から挟む」形は同じ外形寸法でもhが小さくなるので、避けた方がいいでしょう。
ただ、このほうが駆動系を納めやすいことも確かで、必ずしもNGとは言えません(上の案は緑色の薄い部分に駆動系も入れなければならない)。
先ほど無視した、鉛直方向(軸方向)の重力などによる力は、もちろん、設計上は無視できません。
とくに、ボールベアリングはあくまで軸に直角方向の加重を支える設計で、軸方向の荷重にはアンギュラ軸受けなどでないと耐えられませんし、限度があります。
そのため、鉛直方向の荷重については、別途スラストベアリングなどを併用して支える必要もあり得ます。
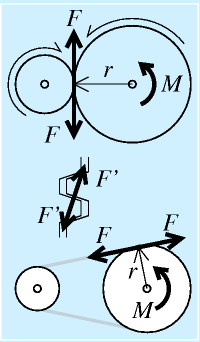 |
| 駆動系の軸に作用する力 |
駆動系の軸にかかる荷重:
最終的に、何かを動かすための軸のほかにも、動力の伝達系の軸にも荷重がかかります。
右図のように、歯車や、ベルト(もしくはチェーン)でトルクMを伝えようとする場合、歯車のかみ合い部や、ベルト(プーリの接線方向とベルト張力)には力Fが作用します。
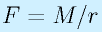
これはトルクと、歯車やベルトの半径によります。
歯車がどこかに飛んでいかないようにするためには、この荷重も軸受けで支える必要があります。
図中には明記していませんが、この力Fがそのまま軸にかかります。
伝達するトルクMがさほど大きくなければ、ほとんど問題にはならないと思いますが、念のために確認はしておいたほうがいいでしょう。
なお、これらの力はむしろ、歯車やベルトの強度のチェックに用いられます。
歯車の場合は、歯面が斜めになっているので、全体的に見て計算したFよりも、多少大きなF'の力が歯面にはかかっています(普通の歯車だと、あまり大きくはならない。圧力角20度で6%増し)。
以上のように、主に力のつり合いの計算で、軸受けに作用する力は計算できます。
ちなみに、荷重をより受けやすくするために…ベアリングを3個以上にすれば?という案はアリですが、その場合、今度は組み立て精度が悪いと軸そのものが回らなくなる超過拘束の状態になりかねないので要注意です。
ロボットの材料
ロボットをつくるためには、当然、何らかの材料を用意しなければなりません。
ロボットの機構部品は、多くの場合それほど多くの選択肢がありません。
たいていの場合は、それぞれの部品メーカが良かれと思う材料でつくっています。
(一般に小型で大出力・高耐力のものほど、特殊で高級な材料が使われる)
ここでは、自ら設計する、ロボットの構造部分などで使用する材料について見ていきます。
材料選びの観点
材料を選ぶに当たっては、主に以下のような観点が重要です。
基本的にすべてに万能という素材はなく(あれば、世の中のものはそれになっているはず)、「多長多短」の特性を見て、譲れないところは譲らず、妥協するところは妥協して選びます。
- 強度:
言うまでもなく、構造材では強度が重要。
不足すれば破壊する。ただし一般に、残りの性質が似たような材料では強度が高いほど高価である。
- 価格:
試作、少量の場合はさほど問題にならないが、大きなものだったり、製品としてつくることを考えると、価格は重要な要素となる。
- 加工性:
一般に材料に対して追加工を行うため、「加工のしやすさ」は、加工に要する時間、加工代金や精度に関わってくる。
単純に堅い材料ほど加工が大変なようにも思えるが、柔らかい材料は「高精度な」加工が難しかったり、樹脂材料では加工時に切削熱で柔らかくなったり融けたりするものも多い。
- メンテナンス性・耐食性:
長期間使用するものの場合、材料の劣化のしやすさと、その劣化防止のための手間が重要となる。
たとえば、材料としては総合的には良好な鉄系の材料は、錆びる。
錆び防止のためにメッキや塗装を行うが、それにも限度があり、ペンキの塗り直しなどが必要となる場合があるほか、傷が付くとそこから錆びることもある。
工作機械など、むき出しの必要性がある場合は油膜で覆うなどのメンテが必要である。
- 供給形態:
その材料は、どういった形で入手できるのか、ブロック材か板かパイプか、という点も事前の確認が必要である。
当然ながら、設計に影響する。
材料によっては薄板は入手できない、というものもある。
- 入手性:
優れた材料であっても、入手性が悪ければ(買いにくい材料であれば)、使いがたい。
そもそも特殊で入手が難しい場合、巨大なロット単位でなければ買えない場合、などがある。
一般に、入手性が悪い材料は、少量を購入しようとすると高く付く。
加えて、納期も重要である。標準在庫品は数日で手元に届くものが多いが、特殊形状のものなどは受注生産で時間がかかる場合も多い。
- 手触り:
構造材としては考慮する必要はないが、外装に使用する場合はある程度考慮すべきである。
金属材料全般に冷たく、かつ、少しでも角があると(角そのものは丸めていても、後に何かで傷ができた場合なども)さわったときに怪我をする危険性もある。
特に、量産ものではない一品ものや試作の場合には、入手性が一番のネックになることがあります。
ロボットの基本構想ができた段階で、早めに材料の調達手段をチェックする必要があります。
ロボット系で主に使われる材料
ロボット系では主に、以下のような材料が見られます。
金属系材料:
- 鉄系:鋼、鋳鉄、ステンレス(物性はいわゆる鉄とはかなり異なる)
- アルミ系:アルミ、ジュラルミン
- 黄銅(しんちゅう)系:快削黄銅
- 特殊な金属:マグネシウム合金、チタン、チタン系合金
樹脂系材料(いわゆるプラスチック):
- アクリル、塩ビ
- ABS
- MCナイロン
- ポリカーボネート
- その他、エンジニアリングプラスチック(エンプラ)
以下でもう少し、詳細に触れます。
材料の形態
設計する上では、材料の供給形態を知る必要があります。
設計すると言うことは、その先の加工方法を指定することにもつながりますが、そのとき、材料の形状とミスマッチした設計をすると、加工の手間が極端に多くなることがあります。
当然、加工に要する時間(生産性)や加工コストにつながるほか、材料の無駄につながります。
そのため、使おうと思った材料に、適切な形状、寸法のものがあるかどうかを知り、最大限それを加工せずに使うように設計を行うべきです。
以下、代表的な材料の形態を列挙します。
- ブロック(直方体)→削り出し用
- 板材→プレス、打ち抜き、レーザー加工など
- 丸棒、丸パイプ→旋削
- 角柱、各パイプ、アングル、チャネル→(切削)、切断、穴あけ程度
基本的に、すべての材料ですべての形態、寸法があるわけではなく、またあっても購入単位が制限される(長さ100mmで買えるか、定尺=2,000mmなど単位になるかなど)ので、事前に確認が必要です。
金属系材料
- 鉄系材料(主に鋼材):
- ポピュラーな材料である。
- 一般の鋼材はかなり安価。
- 強度は高め(組成によってかなり変わる)だが、密度が高く、重い。
- 一般に錆びる(ステンレスは「錆びにくい」)ため、防食が必要。
防食のためには、塗装やメッキ(亜鉛メッキ=トタン板, SECC板、クロムメッキ)などがある。
防食ができない場合は、表面に油をぬるなどのメンテが必要。
単体でも空気中で錆びるが、他の金属と接触させると、より錆びやすくなることがあるので要注意。
- 一般の機械でよく使われている。
- アルミ系材料:
アルミ系の材料は大きく、普通のアルミ合金とジュラルミンに分けられます。
ともに、「A○○○○」と4桁の数字で表され、数字に応じて「○千番台」と大別されます(アルミ以外に含まれる金属の組成による:性質が変わる)
アルミ:
- 1000番台:純アルミ→アルミ板、アルミ箔など
- 5000番台:Mg系合金。ただ「アルミの丸棒」といって発注すると、5000番台が届く。
- 6000番台:Mg-Si系合金。押し出しによる成形が可能で、アルミサッシなどに使われる。アングル、チャネルなどは6000番台。<押し出しでつくっているもよう
- アルミ全般に強度は低く、特に1000番台はやわらかい。手作業で工作するには疲れないが、柔らかいが故に精度の高い工作が難しく、加工時に綺麗に仕上がらない(ねばっこい材質)。
- 基本的に耐食性がある(表面に酸化膜:不動態ができる)。より耐食性をあげるため(また、表面を堅くするため)アルマイト加工が使われる。
ジュラルミン:
- ジュラルミン(A2017)、超ジュラルミン(A2024)、超々ジュラルミン(A7075)
- アルミ合金に焼き入れ後、放置もしくは多少暖めて、時効硬化で硬くする。
- アルミと比べて引っ張り強さが上がり、超々ジュラルミンでは鋼材(SS400)を越える。
ただし、縦弾性係数は変わらない=力によるたわみなどは変わらず。
引っ張り強さは塑性変形=転位の移動によるもので、ジュラは転位が引っかかるようになって強くなる。
縦弾性係数は弾性変形=結晶の歪みによるものなので、あまり変わらない、と解釈できる。
- 合金にまぜたもののため、アルミに比べて耐食性が悪化する。耐食性向上のためのアルマイトもかかりにくくなる。
- 黄銅系:
黄銅にはいくつか種類がありますが、機械工作用には「快削黄銅」がよく使われます。
鉛を添加した黄銅で、ほどよく堅くなり切削がしやすくなります。(文字通り、快く削れる素材。旋盤とかで削ると癖になる)
- アルミに比べて堅く、手頃な「堅めの」材料
- 鉄に比べては弱いが、極端に錆びることがない(すぐに表面は参加して黒っぽくくすむがそれ以上目立った腐食がない→5円玉が参考例)
- 比重は鉄より重め。
- 歯車やネジの材料になることもある。
- 特殊な合金:
主にコストなどの点で、広く使われているわけではありませんが、軽くて強い材料、としてマグネシウムやチタン系の材料が使われる場合があります。
- マグネシウム系:最近ではパソコンなど電子機器の筐体(ガワ)などに使われる場合が多いほか、(高級な)ロボットのフレームなどでも使用される例が増えている。
アルミよりも軽く(密度が低い)、通常のアルミ合金に匹敵する強度を持つ=同じサイズでより強い。
ただ、超超ジュラルミンなどとは質量当たりの強さで言えば微妙。
- チタン系:軽くて強度が高い。耐食性も高いし不燃性。また生体への適合性が高い。
材料としてはいいところだらけだが、材料の精錬(資源からチタンにすること)が難しいことと、強度故に加工が難しいことから、コストが高く、利用は限定的。
身の回りの機械に使うことは少なく、航空機のエンジンなど特殊な機械などに用いられる。
一方、身の回りでは腕時計など体に触れるものに使われることがそこそこある。
参考:
機械要素 ザ・バイブル:材料物性表
樹脂系材料
- アクリル・塩ビ(ポリ塩化ビニル):
プラスチックとしては入手性がいい。
形状としては板材やパイプなど。
両者を比較すると、
- 強度はアクリルのほうが高い。(堅く、割れることもある)
- アクリルのほうが熱に強く融けにくい。(それでも切削熱で簡単に柔らかくなり、融けてくるので切削速度などに注意)
- アクリルのほうが透明度が高い(水槽などにも使われる)
- 値段は塩ビのほうが安い
と、材料としてはアクリルのほうがよい。
とくに、樹脂材料は「融けること」が切削加工における最大の難点。
アクリル板はレーザー加工でよく切れるが、塩ビは発生するガスの関係でレーザー加工が一般に禁止されている。
- MCナイロン:
日本ポリペンコ社の商標ながら、有名な樹脂。機械にマットな風合いの青いプラスチックが使われていたら、MCナイロンの可能性が高い。
その辺のDIYなどでは買えないものの、業者経由では容易に購入できる。
加工性は良い(融けにくく、削りやすい。やや難しいとも言われるが、削った感じはいい感じだった)。
滑りやすいという特性があるため、摺動部にもつかわれる。
樹脂製歯車の材料になることもある。
板材や丸棒で売られている。
- エンジニアリングプラスチック(エンプラ):
プラスチックのなかでも比較的機械的特性のいいもの。
ABS、ポリカーボネート、ポリアセタール、ポリイミドなど。
その他
- レーザー加工:
レーザー加工は便利であるが、案外アルミが加工できない。
本学のレーザー加工機の場合、鉄板が10mmまで切断できるのに、アルミは3mmが限界(細かい穴などは2mmまで)。
特に、1000番台のアルミはほとんどNG。レーザー加工にかけるなら5000番台のアルミ板が必要。
ジュラルミンも加工能力は30%くらい落ちる(byメーカー談)。
理由はレーザーの反射。レーザーが光学系に反射して痛めるとのこと。
そのため、金銀銅もNG。
- 黄銅と超々ジュラルミンはどちらが「高い材料」か?
ある部品をつくるために、工場と相談して、切削性のよい快削黄銅を使用していた。
が、重いので、同じ部品を超々ジュラルミンでつくることを検討(やはり切削性はわりといい、普通のアルミではつくれないとのこと)。
で、見積をとってみたら、同じ寸法の黄銅の丸棒と超々ジュラの丸棒で値段が同じ(ジュラが僅かに安かった)。ジュラは高級品というイメージがあったが...。
結果、やはりジュラは高かった。1kgあたり(金属材料はよく、kgあたりの値段を考える)の金額では超々ジュラルミンは黄銅の3倍ほどの値段。ただし、密度は3分の1。
同じ体積→(重さは1/3)×(kgあたり3倍)→同じ値段
分かってみれば当たり前。ただ、これで「高い材料」といって避ける理由は無くなった。
往々にして、強度計算の結果ではなく、「形として体積が必要」という場合があるが、そのときには「kgあたり」ではなく「体積あたり」の値段が重要。
それが同じで重さが1/3で、かつ、強度もアップ。こんないい材料はない。
ただ、耐食性があまりわかってないが。
- 熊谷研のロボットの材料選び
基本的に、アルミ系。アルミ板(t1,1.5,2,3)、アルミ厚板(t5, t10, t20)、アルミの押し出しフレーム材(ヤマト製)。
アルミの車輪ホイール削りだし。
その他、ハブ状部品もアルミが多い。たまに黄銅。
ギアボックスはアルミ角パイプにベアリング穴を開けて、パイプそのものを外部ケース兼構造材に。
シャフト系は鋼材(ドリルロッド)。φ2~φ10(最大でφ20)
特に強度がいらないところは、レーザー加工を活用する前提でアクリル板。
レーザー加工を前提にすると、材料に制限はあるが、複雑形状も容易に実現でき、工場の加工の手間も削減でき、良い。ただし、断面は一度熱がかかるのと、完全に垂直にならないので、場合によっては注意。
最近、玉乗りロボットのホイール用に購入していた超々ジュラルミン棒をシャフト系材料、汎用丸棒として転用を試み。
自前ではアルミ丸棒があまり綺麗に削れず、これまで黄銅を使用していたので↑の理由から黄銅の必要が無くなった。
レポート その3
以下の材料の特性を調べ、見やすくまとめよ。
- 系統の異なる5種類以上(明確に違いがあるように、基準としてSS400を含めること)
- 名称(あれば記号番号表記)、 組成、 材料の特徴(文で)
- 縦弾性係数(ヤング率) 引っ張り強さ(引張強度) 密度 ※単位明記のこと
- 価格例(例:板厚○○mm、○○×○○mmで○○円、アングル寸法、1kgあたり他)
注)ヤフオクの価格は使用禁止(相場を無視しているため)。 通販サイトはOK
- 卒研で使いそうな材料は率先して含めること。
- 次回予定のレポート(材力計算)で使うことを想定のこと。
材料力学:部材の強度の確認
ロボット設計と材料力学
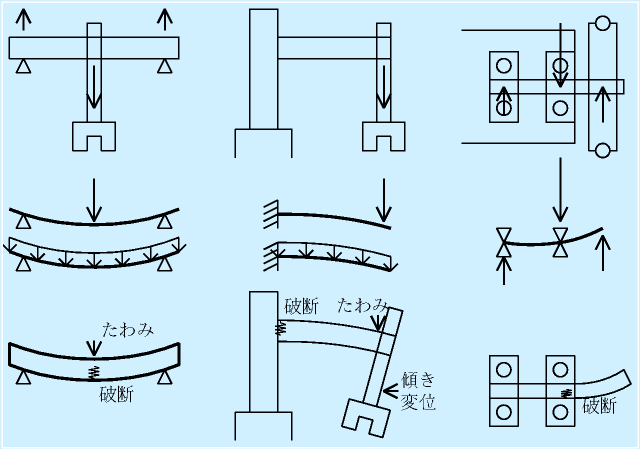 |
| ロボットの構造と材料力学 |
ロボットの構造設計において、材料力学による強度計算は避けて通れません。
もちろん、どの程度重要かは扱いに寄ります。もし、適当につくって確認するだけ、とか、感覚的に絶対大丈夫、というところは計算の必要は無く、念のための概算程度でいい可能性はあります。
一方でぎりぎりまで軽量化したい場合や不安がある場合はそれなりにまじめに計算する必要があります。
別の観点では、コストが重視される量産品ほど、ちゃんと検討する必要があるでしょう。壊れても困りますが、切り詰めて設計することができれば重量が減らせ、その結果使う部品のコストも下げられる可能性があります。
材力を適用して計算することは主に二つあります。
ともに、部材にかかる荷重・設計した形状・材料の特性によって、算出されますが、前者はすぐに思い当たっても後者は見落とすことが少なくありません。
長い部材であれば壊れなくてもたわみが目立ち、その結果、位置精度に影響が出る場合もあります。
右の図は荷重によって部材が影響を受ける例を三つ示しています。
左の例は両端支持のはりを用いた移動クレーン型、中は腕を張り出す片持ち型、右は移動ロボットの車軸部の構造です。
上は模式図、中は構造の主要部に注目した線図、下は部材に生じうる影響です。
ロボットの構造にかかる荷重は、他の部材を支えたり重い駆動装置が乗ったりすることによる集中荷重に加えて、自分自身の分布荷重を考慮する必要があります。
特に、根本に近い部品ほど、その先を支える必要があるため太い構造になり、自身の質量の影響が無視できません。
(その点、車軸は基本的に分布荷重を計算するほど重く長いことは少ない)
材料の許容(構造的、材質的)を越える力が作用すれば、もっとも曲げ応力が高くなるところから壊れます。
多くの場合は、大きな力作用している点ですが、固定端がある場合、固定端の根本には大きな反モーメントなどが生じており、それが原因でそこから破断する可能性は高くなります。
- 移動クレーン型: 支持するという点では有利な形状ですが、それでも油断すると荷重がかかっている部分のした側に負担がかかります。また長くするためにこの形態を選択することが多く、僅かな変形(率)でもたわみとしてみると大きくなることがあります。たわみはある程度計算しうるため、制御で補正することも可能ですが。なお、荷重が中央に無い場合は、程度は小さいものの、片持ちと同じ傾きの問題が生じます。
- 片持ちアーム: この図では柱の部分はたわまないほど強いと無視しています。
アームの付け根には、全体を支えるために大きな曲げモーメントが作用し、それに起因する曲げ応力で破壊する可能性があります。
とくに、「継ぎ目」は単一部材に比べると強度が落ちることも多く、ますます注意が必要です。この影響を避けるには、単一部材で左の方までつきだして、そこに釣り合い錘(単なる錘でなくても制御装置などでいい)を載せて、継ぎ目をなくす、という手もあります。
片持ちは両端支持に比べて弱くなりますが、それ以外にも「傾く影響」が出やすくなります。先端部が傾くことで、上下の位置誤差だけではなく、その先の長さ分だけ水平方向の変位が出る可能性があります。
- 車軸:
車軸は前述のように、車輪の荷重以上の力が、外側の軸受けに作用します。
そのため、単に車輪の荷重だけでは確認できず、軸受けでどの程度大きな力がかかるかを見積もる必要があります。
また、はりの構造としてはこの軸受けのところで曲げモーメントが大きくなり、そこから影響が出ます。
実際に破断まで至らなくとも、回転軸であるため少し曲がっただけでも大きな影響がでます。
加えて、静的な荷重では問題なかったとしても、何かにぶつかるなどの衝撃があると、撃力で強度を超える可能性もあります。
材力計算は次のステップで行うことができます。
- 1:荷重の見積:
前に述べたように、「ロボットの仕様、自重による集中荷重」と「自身の構造の分布荷重」によって計算されます。
後者は使用する材料や、具体的な構造設計によって計算されます。
- 2:生じる曲げモーメントの最大値の計算:
→最大曲げ応力(主に引張)の計算
→材料の強度と比較(弾性変形の範囲内か=降伏応力、耐力)
- 3:はりとしての{たわみ・たわみ角}の計算:
→変形による誤差は精度の要求を満たすかどうか(変位・たわみ角→変位)
主な計算式
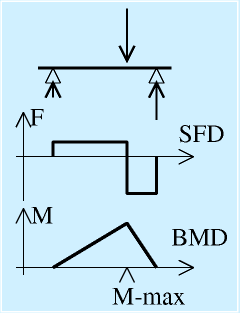 |
| せん断力線図SFDと曲げモーメント線図BMD |
詳細は材料力学の教科書等に譲るとして、ここには最低限の基本計算式を列挙しておきます。
- せん断力 F
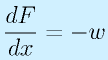
※wは分布加重[N/m]
- 曲げモーメント M
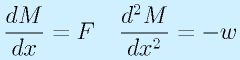
- せん断力線図(SFD)、曲げモーメント線図(BMD):右図に例示
BMDの最大となる点(M-max)で壊れなければ、問題ない。
 |
| はりの断面 |
この最大応力が、降伏応力や耐力を越えなければ問題ないのですが、実際にはそうっと荷重がかかるということはなく、瞬間的な力がかかることが一般的です。そのため、数倍の安全率は見ておいたほうが無難と考えられます。
断面2次モーメントの計算
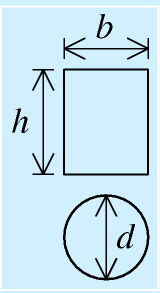 |
| 主要なはり断面 |
断面2次モーメント、断面係数ともにはりの断面を設計した段階で定義式に従えば計算できます。
ただ、実際には特殊な形状を取ることはなく、予め表にまとめられた計算式に実際の数値をいれれば計算できます(材力の教科書や機械工学便覧(「新版」〜もう古い〜ではA4巻pp25)など)。
ただし、一番の基本として、
長方形断面(幅b高さh):
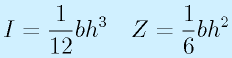
円断面(直径d):
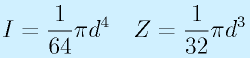
は押さえておきましょう。
力のかかる向きが不定なら対称にすればいいでしょう。ただ長さだけが必要なら丸パイプは一つの手ですが、中にいろいろ詰める場合は加工の手間を考えると角パイプのほうがよいでしょう。
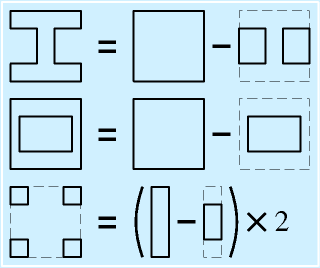 |
| 断面2次モーメントの加減算 |
かなり複雑な形状まで、既存の一覧表には例があります。
それ以上、中をくりぬいたような形状などの場合には、加減算で求めることができます。
右図はその例で、角に4本の柱があるようなケースも引き算と足し算で求めることができます。
これは、断面を二つの領域A,Bに分けると、単に
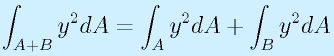
と、積分する範囲を分割できるためです。
なお、あくまで中立面が同じ位置にあることが計算の前提です。そのため、複雑な形状にするにしても、上下、左右対称にはしておいたほうがいいでしょう。
ただし、繰り返しますが、これらの計算ははりに対して単純に上(横)からの力を加えた場合です。ねじる力が生じる場合の強度は別途検討する必要があるので要注意です。
はりの変形
塑性変形でまがってしまわずとも、弾性変形の範囲で問題となる変形をする可能性があります。
とくに精度が要求される場合、関節角度などが十分な精度でも、はりがたわむことで、誤差が出て問題になり得ます。
以下、変形に関わる基本式を記載します。
 |
| 支持の違い |
最終的なたわみの曲線y(x)ははりの曲げモーメントの分布と縦弾性係数、断面2次モーメントと、その支持方法で決まります。
単純に、縦弾性係数が大きい高い材料を使えば、たわみが小さくなります(強度とはまた別であることに注意)。
断面2次モーメントは大きいほどたわみが小さくなり、強度と同様に有利になります(が、単に大きくすると結果的に重くなる危険性)。
比較的単純な支持の例を右に3つ挙げました。
- 単純支持:
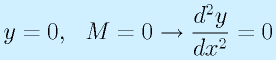
※点で荷重を支えるだけでモーメントを受けられない=0
- 固定端:
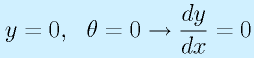
※位置と水平方向であることが固定される
- 自由端:
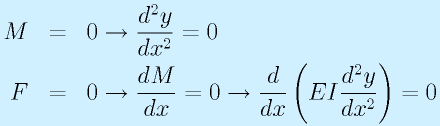
※宙に浮いている=モーメントもトルクも支えられないのでゼロ
これらはすべてy=0を前提とし、固定端も水平方向であることを前提としているので、異なる状況では修正する必要があります。
 |
| 重ね合わせの原理 |
ただし、一般には毎回微分方程式を解く必要は無く、やはり既に計算されている各種はりのたわみ角やたわみに基づいてパラメータを代入して計算すれば十分です(機械工学便覧「新版」A4 pp27など)。
このとき、複数の荷重が作用していて複雑な場合は、各々の荷重ごとにたわみ等を求めて合計する「重ね合わせの原理」を使って求めることができます。
レポート その4
検討中のロボットの中で、曲げに一番弱いと考えられる部材(移動はり、腕部、車軸等)について、以下の手順で妥当性を検討せよ。
(回答の様式は【】内を参考とする)
(1)荷重を明確にする(集中荷重、分布荷重等 ただし、妥当に簡略化する)【線図、数値】
(2)曲げモーメントが最大となる点を示し、そこでの曲げモーメントを求める【図、数値】
(3)以前の検討結果などをもとに、断面2次モーメントを求める【断面図(寸法)・数値】
(4)最大の曲げ応力(引張がわ)を求め、想定している材質の引張強度を超えてないか確認する【計算値・材料値・可否】
(5)最大のたわみを計算する【線図、数値】
以上で、メカ的な部分の検討を終え、制御とのつなぎ目に検討を進めます。
熊谷正朗
[→連絡]
東北学院大学
工学部
機械知能工学科
RDE
[| ]







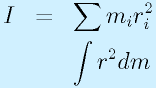
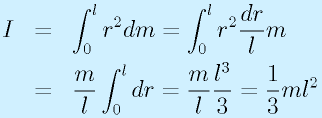


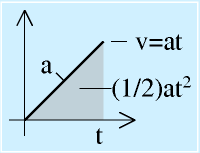

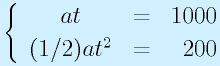 →
→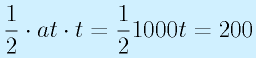 →
→