資料アーカイブ 20140708版
内容紹介
今回はメカトロのうち、メカを作るときに必要になる(かもしれない)材料の選択と材料の強さについての基礎知識です。
より身近には、なぜ、物干し竿はぎっしり詰まった棒では無く、パイプなのか、を説明づけます。
ものを作る場合には様々な材料を用います。
たとえば、玉乗りロボットを作るにあたっても材料の選択をしています。
キーとなる車輪は、当初は黄銅、現在は超々ジュラルミンを素材としています。これは、車輪を構成するローラの形状が多少複雑で、従来から当方で使っていた単なるアルミでは「柔らかいため」加工が難しい、と相談した学内工場で指摘されたことによります。それに対して黄銅、とくに快削黄銅とよばれる材料は、ある程度の強度があり、機械加工で切削しやすい(実際にやってみると、全部削ってしまいたくなるほど、さくさく快く削れます)特長があり、機械部品などの加工にも使われています(黄銅には、磨いてあれば綺麗に見えるという利点も)。ただし黄銅は密度が高く、重たいことが難点です。
軽量化には密度の軽い材料を選びます。アルミは難しいということでも、より硬いジュラルミン系は大丈夫かもということで、超々ジュラルミンに変更しました。これもまた、加工はさくさく削れます(勝手に快削アルミと言っています)。
本来は特殊な高いアルミ合金として利用がためらわれそうな超々ジュラルミンは、実は、同じ体積なら、黄銅とあまりかわらない値段です。
確かにキログラムあたりの値段は3倍程度と高いのですが、密度が1/3程度であるため、同じ体積なら重さが1/3になります。この結果、それにキログラム単価をかけるとあまり変わらないことになります。軽くて強くて(使用可能な強度は一般の鋼を超える程度)値段が同じなら、当然こちらを使います。ただ、実は、他の物の腐食が進むという現象に、あとで会うことになりました。
(実際には、銅系、アルミ系と系統の異なる素材であり、価格比は相互に変動しますので、いまもそうかはわかりません。ただ、軽い分は十分に価値があります。錘として使う場合を除くと)
往々にして、機械部品は「この大きさ・形が必要」というケースがあるため、その場合はこのような損得勘定も成り立ちます。
そのほか、ボディはそれほど強度もいらないので、アクリル板を使っています。これはレーザー加工することを前提にした設計で、箱構造を作ること無く、ネジ棒をつかって層状に積み上げる構造になっています。
下の球はボーリング球ですが、摩擦向上のためにスプレー式のゴムを塗り重ねてあります。実は、玉乗りロボットの実現の秘訣は、このゴム膜にありました(動画サイトのコメントで、スプレー式があることを教えて頂きました)。
さて、ロボットの材料を選ぶときに何を検討すれば良いか、というと、機械的特性として、強さ・密度・加工のしやすさ・材料の形・摩擦/耐摩耗性などがあげられます。
加工のしやすさは、最終的な手間コストに直結するため、重要な観点の一つです。硬いと加工が難しいのは当然として、上述のように「柔らかい」と加工が難しくなる例もあります。また、一般に少量生産の場合は切削加工で部品をつくりますが、加工前の素材と欲しい形の間に大きな差があると、加工の手間がかかり、かつ材料の大半を削りくずとして無駄にすることになります(リサイクルされるものもあるが)。
そのため、目的に合った形の材料を選ぶ必要がありますが、それと同時に仕入れることができる形状を把握し、それを前提とした設計も重要になります。
加えて、安くて強い鉄系材料には錆びるという弱点があり対策が必要ですし、水気のあるところで使う材料も選び方に注意が必要です。材料はどのような環境で使うか、も考慮対象になります。使い方、たとえば人が触るかどうか、などでも、機械的特性以外に気にすることがある場合もあります。
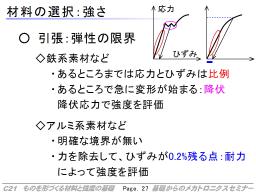
さて、材料の強さと一口にいいますが、いくつもの強さがあります。その中で、代表的な強さが、引っ張ったときに壊れるかどうかという強さと、力をかけたときにどの程度変形するかというバネ的性質の強さがあります。
壊れるかどうかの強さは2種類あります。一つは文字通り、材料がどのくらいの力で切れてしまうかです。もう一つは、一度かけた力を抜いたときに、元の形に戻るかどうかという強さです。力を抜いたときに戻る範囲の変形を弾性変形、戻らない、継続的な変形を伴ってしまう変形を塑性変形といいます。
材料を使う場合は、大半の場合はこの弾性変形の範囲で使わなければなりません。
(例外の例、自動車は事故時に敢えて塑性変形しやすいようにつくることで、衝突のエネルギーを変形のエネルギーに変換して、乗客の安全を高めます。)
いずれの材料も、その弾性の限界があります。鉄系の材料などでは、その近辺で明確な変化が現れます。材料を引っ張っていくと、あるところまでは力と伸び(応力とひずみ)が比例していますが、あるところで同じ力のまま大きな変形が起こる点があり、降伏といいます。この降伏のところを弾性の限界として評価指標にします(実際には若干の違いはある)。一方、アルミ系の材料などでは、明確な変化は無く少しずつ塑性変形が進みます。そのため、力を除去したときに0.2%の変形が残る点を、耐力と呼んで、評価に使います。ただ、この点ではすでに若干の変形は生じてしまうので、実用的には余裕を見て使う必要があります。
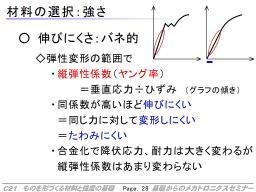
もう一つの強さは、力に対する変形の大きさです。弾性の範囲では、金属材料は、力と伸びが比例する関係にあります。
そこで、力を断面積で割った応力 と 伸びを比率で表したひずみ の比率を縦弾性係数(ヤング率)として、この特性を表します。
縦弾性係数が大きいほど、伸びにくい、つまり、バネ的に見れば強い材料になります。
材料の特性をみると、降伏応力・耐力が強い材料と、縦弾性係数が大きい材料、両方、と様々です。とくに、材料の改良のために行う、他の元素を混ぜることによる合金化では、降伏応力・耐力を大幅に改善する例がいくつもありますが、縦弾性係数はあまり変わらないようです。
このように、材料固有の強さがありますが、部材として使う場合は、断面の形状が重要になります。
棒状の物に何カ所か力がかかるような物を「はり」といってモデル化し、どのような力がかかると(1)壊れるか(降伏応力・耐力と関連)(2)たわむ(弾性変形する、縦弾性係数と関連)かを計算できます。そのときにキーとなる数値が断面2次モーメントと呼ぶ数値です。この値が大きいほど、壊れにくく、たわみにくいものになります。
この断面2次モーメントは、たとえば、
幅がbで高さがhの長方形断面の棒では(1/12)b*h*h*h
直径がdの円形断面では(π/64)d*d*d*d
のように計算式が求められています。同じ形でも、縦長に置いて使う場合と横長において使う場合は、縦長の方がこの値が大きくなります。
また、パイプ状にする場合の計算もあり、同じ断面積(=はし自身の重量に直結)では、パイプにする(中を抜く)ほうがこの数値が大きくなる=強くなります。物干し竿が丸いパイプになっているのは、一つには軽く、強くできるという意味があります。角パイプではなく丸パイプである理由はこの計算ではあまり説明がつきませんが、かける物への影響を考えると角はないほうがよく、かつ平らな面があると雨がたまったりするという問題から、と想像されます。
鉄骨などでよく目にするH型工型の形状も、同様に断面積あたりの強さは増します。
右の図中の写真は、実際に、断面2次モーメントの異なる棒に、力をかけてみたときの曲がり具合です。
単純な四角断面であれば、正方形を1とすると、横に2倍にすると、断面2次モーメントは2倍=たわみが半分になります。
縦長に2倍にすると、上の式からも分かるように、8倍になります。その結果、たわみはかなり小さくなります。
(実際には単純な断面ではないため、メーカの数値によると、1:2:7.2程度、それでもかなり縦長は強くなる)
さて、では、単に正方形の棒を2本組み合わせるとどうなるでしょうか。横に2本は単に2倍、これは当然に思えます。
縦に積んで2本の場合は、先ほどの8倍では無く、ただの2倍にしかなりません。
これは、一体の材料と、個別の材料では意味が違うことを示しています。強化が目的であれば、単に2本積み上げるのではなく、単一の材料を選び直すか、もしくは同時に変形するようにしっかり結合するか(とはいえ難しい)のような対応が必要です。
このように、材料を選んだり、断面を工夫することで、強度を上げることはできます。
ですが、限度があり、自重が増えることでデメリットが生じる場合もあります。
まずは、はりに無駄な力がかからないような設計とすべく、設計を見直した方がいいかもしれません。
参考情報:
機械工学便覧、ネットで見つかる各種計算式、材料特性情報
資料アーカイブ 20141014版
- WEB版
- PDF版(1スライド/1ページ) (2014/10/14, 3,381,596 bytes)
PDF版(4スライド/1ページ) (2014/10/14, 1,958,635 bytes)
PDF版(8スライド/1ページ) (2014/10/14, 1,677,567 bytes)
各種計算例 表計算ファイル(xlsx) (2014/10/14, 395,373 bytes)
内容紹介
今回は、メカトロの一分野なのか?という数学です。
数学はいわゆる技術ではありませんが、多くの技術の背景にあり、それを考え、説明するための道具としては非常に重要です。
そこで、普段、私自身が使う数学をほぼ全て(ジャンル的にはこれで9割以上をカバー)、実際に使うシーンをベースに紹介してみました。
そもそも、ここで紹介するメカトロで使う数学と、中高大で教育される数学はなにが違うのかといえば、(一部に表記や考え方の違いはありますが)根本的には同じものです。
ただ、教育の数学は「この先なにかで必要になったときに使えるように」汎用にかつ順序よく積み上げていくのに対して、技術ではその一部しか使いません。
数学の講義では何時間もかけて、その演算方法の基礎から「正しさ」(証明)を教えていくのに対して、技術的には適用するために原理を知り、結果を得るために計算するだけです。ある意味「ハサミは買ってきてパチンとやれば切れる VS 良く切れるハサミを作るには原理も理論も材料も必要」という「技術を使う側 VS その技術を生み出す側」と似た構図で、一般的な数学教育は「生み出す側」に「も」なれるようにするためのもので、我々は「使い方」があればいい、と言えます。
もちろん、原理をいろいろ知れば活用の世界が広がることは言うまでもありませんが、最低限使えるところまで、であれば、かなり限定されます。
そこに、いまからでも、使えそうな数学を知り、修得したり思い出したりすることの意義とチャンスがある、ということが、今回の念頭にあります。
さて、今回は使うシーンから数学を紹介する形を取りました。そのため、
- 機械の可動部の図形的な解析(ここをこの角度にするとあっちがあの位置に,的)
- 機械の可動部の速度的な解析(この軸をこの速度で回すとあっちの速度は?、的)
- 機械や回路の周波数的な反応(機械振動の検討やフィルタ回路の設計)
- 3次元空間の設計と解析(立体的な装置、動作のための数学的表記)
という四つのケースを用意し、それぞれで使う数学的な手法を紹介しています。
機械の図的な解析では、クランクスライダ機構を例にしました。
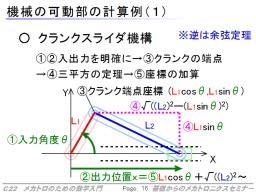
クランクスライダ機構は、右の図のように、軸の回転に伴って動く棒のクランク、なにかにガイドされて直線的に動くスライダ、それを接続するリンク(コネクティングロッド:コンロッド)からなり、それらは自由に回転する関節でつながっています。
クランクを回すことで、コンロッドで引っ張られる/押されてスライダが動きます。逆に、スライダを動かすとクランクが回ります(ただし、スライド動作だけでぐるぐる回転するかは別の問題)。
この、クランクとスライダの関係を考えてみます。
まず、座標を設定します。
各点の位置などを数値で表す基準とするため、直角な2方向の軸と、原点(座標が0,0になる)を定めます。ここでは、スライダの方向にX軸、原点はクランクの回転軸としました。
次に、三角関数を用いて、クランクの角度に伴う、端点の位置を、出します。
三角関数は直角三角形の辺の比で定義されるものですが、拡張され、このように「長さ+方向」から座標を出すことに使えます。
いろいろな計算法則がありますが、その中でも(この機構では使いませんが)余弦定理はメカ設計で使い道の多いものです(メカトロセミナーでは今回が3回目の登場)。
最後に、三平方の定理で、コンロッドの長さを斜辺、クランクのY方向位置を一辺とする直角三角形を考え、残り一辺を計算します。
この長さと、クランクのX方向位置を加えれば、スライダの位置が求まります。
上の表計算ファイルは、この計算例を含みます。各部の長さを調整することで、動き方の変化が確認できます。
今回は、クランクの回転軸から直線方向にスライダが動くようにしました。もし、スライダの動く方向が斜めだったりする場合は、(1)三平方の定理より複雑になるが直線の式と、クランク端点を中心、コンロッド長を半径とする円の式の交点として2次方程式を解く (2)そもそも、スライダにそってX軸を決め、クランクの回転軸の位置をずらす(単にスライダ端点の座標に加算) などで、求めることができます。
さて、たとえば、このクランクの軸を一定速度で回転させたら、スライダはどのように動くでしょうか。
ここで出てくるのが微分の計算です。
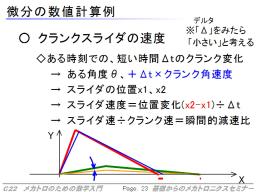
微分の考えは、「ごく短い時間での移動量をその時間で割れば、その瞬間の速度が得られる」というものです。数学的には「ごく短い時間」を極限まで短くすると、ということを考えますが、実際には「妥当に短かい」ようにすれば、微分値に相当する値を得ることができます。
スライダ位置を数式で求め、これを数学的に微分することでもスライダの速度はわかりますが、ここではより簡単な数値的な方法を紹介しました。
まず、速度を求めたいあたりの角度で、一度スライダの位置を計算します。
つぎに、「クランクの回転速度×適当に短い時間」(適当に小さい角度でも可)だけ。クランクの角度を変化させ、そのときのスライダ位置を計算します。
このスライダ位置の変化量を、その時間で割れば、それがスライダの速度になります。
また、スライダの速度÷クランクの回転速度、または、スライダの変化量÷クランクの変化角度、を計算すると、その状態における瞬間的な減速比を求めることができます。
減速器は、減速比だけ速度が遅くなると共に、力がその逆数(1/減速比)だけ大きくなる性質があります。つまり、この瞬間的な減速比が小さくなるところ、クランクを動かしてもスライダがほとんど動かなくなるところ(クランクが水平方向の2箇所)では、力が大きくなります。
それを利用してなにかを押し込む動作などに使われることもあります。
これを表計算ファイルではグラフ化してあります。たとえば、クランクを200mm、コンロッドを210mmにすると、間欠的に押し出すようなスライダ動作が得られるなど、調整することができます。一方、クランクを210mm、コンロッドを200mmにすると、グラフがおかしくなるとともに、計算値にも妙な表示がでます。これは、計算ができなかったことを意味しますが、よく考えてみれば、この長さの条件ではメカ的に動かない場所が出てきます。そのようなことも分かるわけです。
上のクランクスライダの例は、位置関係だけで(幾何学的に)決まる例ですが、速度や力の影響を目に見えて受ける運動もあります(クランクスライダも当然影響ありますが動きという点では目立たないだけ)。
たとえば、バネやダンパの含まれるものは、その代表例です。
この場合は、運動方程式や力の釣り合いを考えることになります。
たとえば、自由に動く台車にバネ、ダンパがついているところに、外から力を加えると、
外力、バネ×移動量、ダンパ×移動速度、質量×加速度(ニュートンの運動の法則)
が作用しますが、これらは、
外力 バネ×位置、ダンパ×位置の時間微分、質量×位置の(時間微分)2回
となり、力と位置と微分の式になります。このような式を微分方程式といっています。
微分方程式を直接解くには面倒な計算が必要です(解けない場合も多い)。
一方、微分の反対の積分を、数値計算で行う方法があり、それを併用すると
現在の外力や位置など→加速度を計算→積分して速度→位置
と順次求め、また、加速度の計算に使う、という繰り返しで、ある程度の結果を得ることができます。
いわゆる「シミュレーションソフト」には、内部で微分方程式を構築し、それをこのような計算で算出するものが多くあります。
さて、この微分方程式は世の中の様々な現象を表しますが、その答えとして三角関数が出てくる場合があります。たとえば、振り子の運動や、バネでものをぶら下げたときの往復振動は、正弦波の時間関数の形なります。
三角関数は三角形の辺の比という定義でしたが、それと共に、自然界の「ピュアな往復」でもあります。
そのため、様々な対象の解析手段として「正弦波を入力して、どんな結果が帰ってくるか」を調べる正弦波応答、これを様々な周波数で調べて全体的な特性を得る周波数応答が、制御やアナログ回路を始め、さまざまなところで使われています。
正弦波応答として、「線形」という特性をもつ対象(わりと多い)に正弦波を入れた場合には、同じ周期・周波数の正弦波が出てきます。
ただし、大きさと時間のタイミングは変わることがあります。
変化した大きさの比(出力振幅÷入力振幅)を増幅率といいます。タイミングのずれについては、その正弦波の一周期に対する比率で表し、一周期を360度として角度で表したものを用い、位相といいます。たとえば、波が1/4周期だけ時間が後ろにずれていたら「90度遅れ」「位相マイナス90度」といいます。
この、増幅率と位相は、実験をしたり、上記の数値計算でも求めることができますが、別の計算方法があります。
増幅率と位相を計算するために、ラプラス変換という手を使います。
これは原理などは難しい数学ですが、使うだけなら便利な道具です。
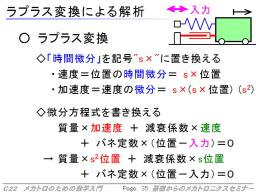
まず、微分方程式をラプラス変換します。ラプラス変換では「時間で微分する」という操作を「sという文字をかける」という操作に置き換えます。
たとえば、速度は「位置の微分」なので「s×位置」になります。加速度は「位置を2回微分」なので「s×s×位置」になります。
このようにすると、外からの入力と動作である結果の間が、微分の関係ではなく、「sで書き表した式」になります。
つぎに、sの部分を「jω」もしくは「2πfj」に置き換えます。fは周波数[Hz]で、ω=2πfは角周波数[rad/s]で、入力しようとする正弦波の周波数から決めます。
「j」は虚数単位と呼ばれるもので、「j×j=-1」となる特殊なもので、これをつけると「虚数」という数値になります。
これと通常の数値「実数」をあわせると複素数というものになります。
※数学では虚数単位は「i」ですが、工学分野では「i」が電流を表すものとして頻繁に使われるためか、「j」が代わりに使われます。
複素数は図形的な性質もあります。2次元の座標で、横軸を実数、縦軸を虚数部分とすると、2次元上に数値を置くことができます。
原点からの距離=√(実×実+虚×虚)と、その方向tan-1(虚÷実):偏角という:を求めることができます。
微分方程式をラプラス変換し、sをjω、2πfjで置き換えたものを計算します(複素数の計算方法は略)。その結果、複素数が出てきますが、これの大きさと偏角を求めると、大きさがそのまま増幅率、偏角が位相を表すという不思議な(でもちゃんと理論的には裏付けされた)関係があります。
これによって、微分方程式さえあれば、正弦波応答、周波数応答を得ることができます。
このようにして得た周波数応答は、時として、増幅率が100倍から0.01倍など広範囲に変化する場合があります。100倍にとって、0.1倍や0.01倍は取るにたらない小ささ・違いですが、一方で、「(1/10)にできる」「(1/100)にできる」といった場合には大きな意味合いを持ちます。たとえば、ノイズを除去したいという場合などに。
このように桁まで変わるような変化を表すには、対数がよく使われます。
また、対数を利用して変換する「デシベル」[dB]という値もよくつかわれ、回路や制御の分野では「ゲイン」というとこのデシベルの値をさすことが多くあります(ゲインという言葉自体は増幅率などの意味をもつ)。
ここまでは、主に、平面的なもの、単なる値の時間変化についてですが、ロボットの設計などでは、立体的なもの、複雑に運動するものを扱うために、3次元の検討をする場合がよくあります。そのときに無くてはならないものが「ベクトル」「行列」という手段です。
ベクトルも行列も使い道はいろいろありますが、立体を表すために限定すると、ベクトルは空間での位置や方向を規定するために、数値(数式)を三つセットにしたもの(3次元の場合、2次元ですむなら二つ)、行列は、このベクトルを回転させるためなどに用いる、数値を3×3で9個並べたものです。
空間を扱うと文字が多くなるのでまとめて書くのに便利、また、ベクトルや行列の演算はコンピュータなどに任せてしまうことが多く、それならひとまとめでプログラムを書いた方が楽、など、「すっきりさせる」効果もあります。
このベクトルの演算は、数値的に計算するためにももちろん使いますが、さまざまな仕組みを考えるときもよく使います。最近は、何かものを動かす原理を考えるときは、落書きの上にベクトルを書いて、その関係を考える作業から始めることも多くあります。
そのときに使う演算で代表的なものに内積と外積があります。
内積は二つのベクトルから一つの数値(ベクトルに対してスカラという)を作る演算で、二つのベクトルが直角かどうかを判定したり、あるベクトルから、ある方向の成分を抜き出したりすることに使えます。
外積は二つのベクトルから一つのベクトルを作り出しますが、もとのベクトルのそれぞれに直交するベクトルができるという特徴があり、空間のなかで、適当な方向の点や面などから、それに垂直な方向を計算するためなどに使えます。
また、空間での回転の計算として、「ある軸まわりの角速度」による「ある場所の速度」や、「あるところにかけた力」がどのような「ものを回転させるトルク」になるかの演算にも外積が使われるため、空間での回転運動を考えるときには必要になります。
このベクトルは、回転行列という、cos,sinの入った特別な行列によって回転させることができます。
たとえば、マニピュレータのように曲がる関節が一つあると、そこに回転行列が一つできます。
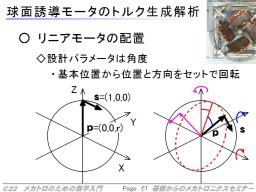
また、球状・円筒状に、対称性のある機械を作ろうとした場合に、どこにものを配置するかを具体的に計算することができます。
いまの時代は3次元CADなどでもそのような作業はできますが、数値的にきっちり出したい場合、それがそのあとのメカの運動計算に必要になる場合などは、行列などを用いて計算した方が便利が場合があります。
その実際に活用した例として、球面誘導モータを紹介しました。
今回は「熊谷が使う数学テクニックの大半の概要」を目指したため、このベクトル・行列までいれましたが、実際にはこれは概要だけでも解説すべきことが多く、本当にかする程度しか用意できていません。もし、関心があれば、ロボットの数学のページもご覧下さい。
ここまでの計算は、いまどきのプログラミング言語や表計算ソフトでは概ね可能です。複素数や行列ベクトルは特殊なものですが、表計算ソフトでも(ちょっと癖はありますが)扱えるような手段が用意されています。まずはなにかあったときに試してみると良いともいます。
というわけで、今回は数学を題材にしました。
勘と経験があれば、実際には、数学は必須ではないケースも多くあります。ただ、「なぜそうするのですか?」「それが最適ですか?」という疑問質問に対して説明しようとしたときには、数学に基づくと説明が楽になります、少し修正した方がより性能が出ることに気付くケースにもあり得ます。また、実物や図面の上での試行錯誤を予めちょっとした計算で済ませて一発で目的のところに持ち込むということも多いため、普段、なにかを作ろうという時には、「落書き+座標/ベクトル/補助線+数式+表計算」というパターンで、それから図面を引き始めています。
「数学」というネタはメカトロセミナを始めたときにあった一番最初の企画案にはすでに盛り込まれていたのですが、これを実施していいものかという不安から、ずっと棚上げされ続けていました。今回もまた大幅にオーバーランした2時間コースになってしまいましたが、メカトロセミナ過去最多級の方がいらっしゃり、かつ、最後まで熱心に聞いて頂きました。関心の高さを感じたと共に、ほっとしました。
資料アーカイブ 20141216版
- WEB版
- PDF版(1スライド/1ページ) (2014/12/16, 6,509,733 bytes)
PDF版(4スライド/1ページ) (2014/12/16, 3,510,453 bytes)
PDF版(8スライド/1ページ) (2014/12/16, 2,370,593 bytes)
- 関連動画:
3次元CADによるリンク機構の組み立て例(WMV) (2014/12/15, 32,127,373 bytes)
同 Youtube
ロボット発進用ゲート機構(WMV) (2014/12/15, 47,188,530 bytes)
同 Youtube
内容紹介
今回は機械の3次元設計に関する基礎と、最近話題になった3次元プリンタを含む3次元加工についての内容です。
そもそも、我々メカトロが相手にしているのは3次元です。横・奥行・高さの移動があり、その中での回転があります。
さまざまな設計で、水平面内での動き(あるいは鉛直面内)がメインになることは多いと思いますが、それに上下(水平)方向の動きが加わります。
そのような機械を長らく、2次元、以前は紙上で、その延長の2次元CAD上で設計してきました。
3次元CADも以前からはありましたが、今日のコンピュータの発達と共に、極端に規模が大きくなければあまりストレス無く使えるようになり、普及が進んでいます。とくに、3次元の加工技術の発達と共に、その必要性が高まっています。
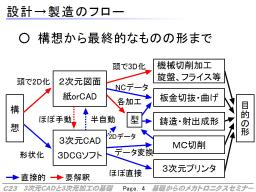
最終的な成果物が3次元でありながら、2次元で設計するという場合には、途中で3次元の2次元情報化、2次元の3次元かが必要なります。
前者は主に設計者の頭の中で行われ、最終的に作りたいものの形状を2次元の図面(3面図など)の形で書いていきます。
それに対して、それを実際に加工する段階で解釈し、3次元のものを作り出していきます。
根本的に、3次元のものを2次元で表すときには情報が減るため、逆に2次元の図面から3次元にするときには、その1次元分の復元作業が必要で、そこで誤解釈が起きないようにするために、製図の書き方、テクニックがありました。
一方、3次元CADは最初から3次元の情報のまま持ちます。また、そのデータを変換することによって、数値制御(NC)の工作機械にそのまま渡し、その設計データの通りに複雑形状の削りだしなどができることが利点です。逆に言えば、そのような加工をしようと思った場合には、3次元CADで設計する必然性があります。話題の3次元プリンタもまさにその類いです。
加えて、ある程度以上の3次元CADには、コンピュータ内での組立機能があります。
個々に設計した部品を、穴と軸、面と面などの接合条件を設定することで組立、また回転軸や直動などの条件設定をすると画面内で動かすこともできます。
また、組み立てたもので、部品間の最短距離や、干渉している場合はその重なり具合などを解析できます。
頭の中で考えたり、実際に作ってみてあたらないことを確認したり、もしもの場合は削ったり、という従来の苦労を、コンピュータでの設計段階でかなりすますことができ、動きのあるような装置を作る場合にも効果的です。
パラメトリック型、と呼ばれているCADでは、寸法の変更で部品形状を変えることができ、リンク機構などの微調整も可能です。
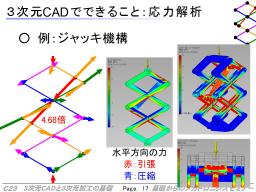
そのほか、部品の力学的特性(密度→質量、慣性モーメントなど)を求めたり、各部にかかる力の分布の解析とその評価による部材強度の検証が可能な製品もあります。ただ、業界でデファクトスタンダードがはっきりしないこと、高価なソフトウエアであることから、導入時は取引先での導入ソフトの確認などもしたほうがよいでしょう。
このように設計したデータを元に部品化する場合、3次元特有の手段がいくつかあります。
マシニングセンタ(MC)という、大型のNC切削加工機はを用いる場合、金属の加工物可能で、強度や精度などを確保しやすくなります。
ただし、1個ずつ削り出すため、加工時間が長く、生産性が良くありません。そのため、一品ものには向きますが、量産に使う場合は別の手段の検討も必要になります。
射出成型は樹脂部品の製造で幅広く使われている手段です。金型を用意し、そこに加熱した樹脂に圧力をかけて流し込みます。
金型の精度には依存しますが、比較的精度がよく、かつ、短時間で連続して製造できるため、生産性が高く、身の回りの製品によく使われています。
ただし、金型のコストが高いため、少量生産には向きません。最近では、プロトラブズ社のように手頃な?価格での射出成型サービスも出てきています。
3次元プリンタは、実は20年以上の歴史はあるのですが、最近急に注目されるようになってきた成形手段です。
樹脂を融かしながら絞り出して成型するFDM式、紫外線で硬化する樹脂を用い、液中で照射して固めたりインクジェット印刷しながら固めたりする方法、金属などの粉末にレーザを照射して固めていく方法、石膏にインクジェットで印刷して固めていく方法などさまざまな方法がありますが、一般的には、目標とする形を一層ずつ形づくっていきます。
それゆえ、成形の精度、強度的な制約がある一方で、作り出せる形状にあまり制約はありません。たとえばMC切削の場合は加工の刃物(エンドミル)が外側から届くような形状でなければ加工できません。射出成形でも低コストにするには、二つの金型が両側にぱかっと開いて取れる形状、それに追加でスライドして抜けるような型でなければなりません。それに対して、3次元プリンタだと複雑な内部構造を作り込んだり、ある程度可動な組立済の形状を作り出すことができるものもあります。
この点は3次元プリンタを試作段階で使うときの要注意点です。
最終的に他の手段で作る予定がある場合は、必ずそれらの手段での制約を考慮しなければ、プリンタでは作れたけど本番で加工不能、もしくはコストが想定外ということになりかねません。
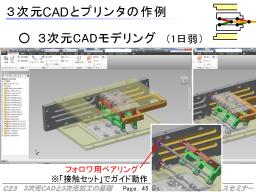
ここでは、以上の実例として、安価なFDM式3次元プリンタ(
XYZプリンティング社製ダヴィンチ)と、3次元CAD(
Autodesk社Inventor pro)による設計事例を示しました。
まず、機構の構想を実現するために必要な部品をCADで設計し、CAD内で組み立てて機構のチェックを行います。
この部品をそれぞれ3次元プリンタで出力して組み立てています。
アイデアはあっても、なかなか形にする手段が無かった、ということを試すにも、3次元CADとプリンタの組み合わせが効果的であることが確認できました。
このセミナーを実施したころ、研究室では学生さんの卒業研究が佳境にさしかかっていましたが、この3次元CAD+3次元プリンタという組み合わせは、当研究室の卒業研究における開発の方針を一変させました。
さかのぼること10年ほど前、大学の学内工場にレーザー加工機が導入されたときに、研究室内の設計基準が変わりました。
それまでは、フライス盤や旋盤による切削が前提の設計をしていましたが、レーザー加工機は板材をCADの設計通りに切り抜けるため、形状の制約を気にせず目的に合わせた設計で、板状の部品をメインとした機械設計になりました。
今回はそれに匹敵する変化がありました。目的とする形を複雑さをあまり気にせずに作り出すことができるため、形状の目的に応じた最適化がしやすくなりました。
また、3次元CADで設計してそのまま3次元プリンタに投入して部品を製作、組立試験をして不具合が見つかったところで設計に反映して、と開発の1サイクルが劇的に短縮し、それまでは1,2回の試作が限度であった開発で、より多くの改善を行えるようになりました。
ただし、従来の加工をすることをあまり考えないこと、数値データさえあればよいため図面としての仕上がりをあまり気にしなくなってしまったという点は弊害だとは思います。
従来型の機械設計になれている方が活用すれば、非常に強力なツールにはなろうかと思います。
資料アーカイブ 20151208版
- WEB版
- PDF版(1スライド/1ページ) (2015/12/08, 9,801,822 bytes)
PDF版(4スライド/1ページ) (2015/12/08, 5,204,975 bytes)
PDF版(8スライド/1ページ) (2015/12/08, 3,431,886 bytes)
- 関連動画:
3次元CADによるリンク機構の組み立て例(WMV) (2014/12/15, 32,127,373 bytes)
同 Youtube
ロボット発進用ゲート機構(WMV) (2014/12/15, 47,188,530 bytes)
同 Youtube
3自由度球体駆動装置 Youtube
内容紹介
今回は
第23回:3次元CADと3次元加工の基礎の改訂版です。
ご要望を頂いての、初の/最速のリバイバルになりました(メカトロセミナでは今後はこれまでのテーマの再実施も行っていきます)。
基本的な内容は23回と同じですので、本ページの解説は23回のほうをまずはご覧下さい。
研究室に3次元CAD・3次元プリンタを導入して、本格的に使い始めたころに開催した前回から1年、当研究室での3次元CAD・プリンタは大活躍し、いまでは開発に無くてはならない存在になりました。
その意味で、セミナーの方向も、単なる話題性ではなく、より重要性に重点のある方向に重心が移りました。
そのあたりの実例が今回は含まれています。
まず、研究室では、私のプロジェクトも、学生さんのプロジェクトも3次元設計が前提となりました。
これは形の確認をしやすいこと、3次元プリンタで最終版の作成もしくは動作等検証用の試作版の製作をするようになったことがあります。
加えて、学生さんの様子をみると、2次元CADにくらべて使えるようになるまでも早く、かつ、設計結果の水準も上がる効果が見られたことによります。
現在では、「まず、強度は度外視して、アイデアを形にするために、最初にプリンタでつくること」を優先して、その後、強度が必要なところは従来の設計、機械加工に置き換えていく方針を採っています。
いろいろと利点は多いのですが、一つの懸念として、依然として主流な2次元図面や従来の機械加工との互換性が失われやすいことがあります。3次元設計・3次元プリンタの自由度の高さをそのままフルに使ってしまうと、2次元では表現できない・一般的な機械加工手段では加工できない形状が簡単にできてしまいます。
その点は気を使いながら活用するようにしています。
今後はますます、機械工作の実習体験などが、こういった3次元活用の重要な基礎になっていくのではないかと思います。
一方で、私自身の変化としては「3次元プリンタで出力するから」という割り切り、最適化が当たり前にできるようになったことです。
1年前の事例としてあげた、「ロボット発進ゲート」は、3次元プリンタで作りつつ、実際にはほぼ従来型の加工手段で作れるような設計になっていました。
これは、プリンタを使いつつも、従来型との互換性の維持を強く意識していたこと、「形を考える」発想の根本がそこにあったことによると考えられます。
一方、今回の事例である、球体駆動装置は、従来型の手段で作ることを無視した設計になっています。
同じようなものが玉乗りロボットの駆動系に使われていますが、以前はアクリル板をレーザー加工で切り抜いて、タップなどの追加工をしたものを組み立てて作っていました。
今回はそれを一体成形しています。その際、切削加工では不可能な形状が何カ所にも現れています(鋳物なら無理すれば作れるかもしれない、程度)。
あまつさえ、組立のネジすら入らないような構造にして、そのネジを締めるためのドライバを挿入する穴を貫通させるという「ひどい設計」です。
ただ、今回の設計意図の実現のためには、これが最適な形状であると考えています。
このような、設計の幅を拡げる手段としての、3次元プリンタも有効ではないかと考えています。
なお、この装置、車輪の部分は主な部分は射出成形の外注で、ハブの部分はプリンタでモータの軸にカスタマイズしてつくる構造にしています。
現時点でまだ、3次元プリンタは試作の域が主で、量産する製品に使うには無理があるようですが、一方で、その有効性は十分で、量産に使えるような技術とする開発が進められているようです。もう何年かすると、ある程度の量産にはプリンタが使えるようになるかもしれません。